湘教版备考2021年中考数学三轮复习专题3不等式与不等式组

试卷更新日期：2021-05-12 类型：三轮冲刺

进入出卷网下载

一、单选题

1. 如果关于x的不等式组 ${\begin{cases} 5 x - 2 a > 0 \\ 7 x - 3 b \leq 0 \end{cases}$ 的整数解仅有7，8，9，那么适合这个不等式组的整数a，b的有序数对（a，b）共有（）

A、4对 B、6对 C、8对 D、9对

查看试题解析
2. △ABC的两条高的长度分别为4和12，若第三条高也为整数，则第三条高的长度是（）

A、4 B、4或5 C、5或6 D、6

查看试题解析
3. 若不等式组 ${\begin{cases} 2 x - 1 < 3 \\ x < a \end{cases}$ 的解集是x<2，则a的取值范围是（）

A、a<2 B、a≤2 C、a≥2 D、无法确定

查看试题解析
4. 公司计划用不超过500万元的资金购买单价分别为60万元、70万元的甲、乙两种设备.根据需要，甲种设备至少买3套，乙种设备至少买2套，则不同的购买方式共有（）种

A、5 B、6 C、7 D、8

查看试题解析
5. 下列说法不一定成立的是（）

A、若a>b，则a+c>b+c B、若a+c>b+c，则a>b C、若a>b，则ac²>bc² D、若ac²>bc² ，则a>b

查看试题解析
6. 关于x的不等式x-b>0恰有两个负整数解，则b的取值范围是（）

A、-3<b<-2 B、-3<b≤-2 C、-3≤b≤-2 D、-3≤b<-2

查看试题解析
7. 若不等式组 ${\begin{cases} x < 1 \\ x > m - 1 \end{cases}$ 恰有两个整数解，则m的取值范围是（）

A、-1≤m<0 B、-1<m≤0 C、-1≤m≤0 D、-1<m<0

查看试题解析
8. 已知关于x的不等式组 ${\begin{cases} \frac{2 x + 5}{3} - x > 5 (1) \\ \frac{x + 3}{2} - t < x (2) \end{cases}$ 恰有5个整数解，则t的取值范围是（）

A、9<t＜ $\frac{19}{2}$ B、9≤t＜ $\frac{19}{2}$ C、9<t≤ $\frac{19}{2}$ D、9≤t≤ $\frac{19}{2}$

查看试题解析
9. 使不等式x－1≥2与3x－7＜8同时成立的x的整数值是（　　）

A、3，4 B、4，5 C、3，4，5 D、不存在

查看试题解析
10. 设a ， b ， c ， d都是整数，且a＜2b ， b＜3c ， c＜4d ， d＜20，则a的最大值是（）

A、480 B、479 C、448 D、447

查看试题解析
11. 将不等式组 ${\begin{matrix} x + 2 \geq 0 \\ x < 1 \end{matrix}$ 的解集在数轴上表示，正确的是（）

A、 B、 C、 D、

查看试题解析
12. 小明网购了一本《好玩的数学》，同学们想知道书的价格，小明让他们猜．甲说：“至少15元．”乙说：“至多12元．”丙说：“至多10元．”小明说：“你们三个人都说错了”．则这本书的价格x（元）所在的范围为（）

A、 $10 < x < 12$ B、 $12 < x < 15$ C、 $10 < x < 15$ D、 $11 < x < 14$

查看试题解析
13. 不等式组 ${\begin{array}{l} 2 x > 3 x \\ x + 4 > 2 \end{array}$ 的整数解是（）

A、0 B、 $- 1$ C、 $- 2$ D、1

查看试题解析

二、填空题

14. 按如下程序进行运算：

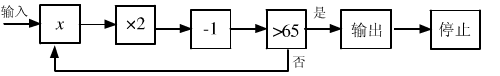
并规定：程序运行到“结果是否大于65”为一次运算，且运算进行4次才停止，则可输入的整数x的个数是．

查看试题解析
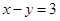15. 已知 .①若 $y < 1$ ，则 $x$ 的取值范围是；②若 $x + y = m$ ，且 ${\begin{cases} x > 2 \\ y < 1 \end{cases}$ ，则 $m$ 的取值范围是 .

查看试题解析
16. 对非负实数x“四舍五入”到个位的值记为（x）．即当n为非负整数时，若n﹣ $\frac{1}{2}$ ≤x＜n+ $\frac{1}{2}$ ，则（x）=n．如（0.46）=0，（3.67）=4．
给出下列关于（x）的结论：

①（1.493）=1；②（2x）=2（x）；③若（ $\frac{1}{2} x - 1$ ）=4，则实数x的取值范围是9≤x＜11；④当x≥0，m为非负整数时，有（m+2013x）=m+（2013x）；⑤（x+y）=（x）+（y）；其中，正确的结论有（填写所有正确的序号）．

查看试题解析
17. 已知关于x的不等式组的整数解 ${\begin{matrix} 6 x + a > 5 x - 3.5 \\ \frac{3 x - 1}{2} \leq \frac{2 x - 1}{3} \end{matrix}$ 共有2个，则a的取值范围是．

查看试题解析
18. 关于x的不等式组 ${\begin{matrix} \frac{x + 15}{2} > x - 3 \\ \frac{2 x + 2}{3} < x + a \end{matrix}$ 只有4个整数解，则a的取值范围是．

查看试题解析
19. 已知：不等式2x-m≤0只有三个正整数解，则化简 $\sqrt{（ 4 - m ）^{2}}$ +|m-9|= ．

查看试题解析
20. 若不等式组 ${\begin{cases} x - a \geq 0 \\ 1 - 2 x > x - 2 \end{cases}$ 有解，则a的取值范围是

查看试题解析
21. 对于任意实数m、n，定义一种运运算m※n=mn﹣m﹣n+3，等式的右边是通常的加减和乘法运算，例如：3※5=3×5﹣3﹣5+3=10．请根据上述定义解决问题：若a＜2※x＜7，且解集中有两个整数解，则a的取值范围是

查看试题解析
22. 若不等式组 ${\begin{cases} x + a \geq 0① \\ 1 - 2 x > x - 2② \end{cases}$ 无解,则实数a的取值范围是

查看试题解析

三、计算题

23. 解下列不等式组

(1)、 ${\begin{matrix} 2 x - 2 > \frac{1}{2} (x - 7) + 1 \\ \frac{2 x - 5}{3} + 3 < \frac{x}{5} + 2 \end{matrix}$

(2)、 ${\begin{matrix} 4 x + \frac{2}{3} < \frac{x - 8}{5} + 2 \\ 2 - \frac{x}{3} > 3 - \frac{x}{2} \end{matrix}$

(3)、 ${\begin{matrix} 1 < \frac{2 x - 5}{3} < 3 \\ (x - \frac{2}{3}) + 5 \geq 2 x - \frac{3}{2} \end{matrix}$

(4)、 ${\begin{matrix} \begin{matrix} x - 1 > - 3 \\ \frac{x}{2} - 1 < \frac{x}{3} \end{matrix} \\ 3 < 2 (x - 1) < 10 \end{matrix}$

(5)、 ${\begin{matrix} \begin{matrix} 2 x + 3 < 9 - x \\ 6 x - 1 < 5 \end{matrix} \\ 2 - x \leq 3 x + 7 \end{matrix}$

查看试题解析
24. 解下列不等式

(1)、2(x-1)-3x>4(x+1)+5

(2)、 $\frac{x + 1}{3} - \frac{x - 3}{2} > 5$

(3)、 $\frac{1}{3} x - 3 + \frac{2 x - 6}{4} < - 3 x$

(4)、 $3 x + \frac{1}{x - 2} + 2 > x + 4 + \frac{1}{x - 2}$

(5)、 $\frac{2 x - 1}{3} - 1 \geq \frac{3 x + 2}{6} + \frac{x}{2}$

(6)、 $5 - \frac{x}{2} \geq 3 \frac{1}{2} - (\frac{4 x + 1}{8} - \frac{x + 2}{4})$

查看试题解析
25. 解下列不等式

(1)、4x-2+ $\frac{1}{x - 5} > \frac{1}{x - 5} + 3 x + 2$

(2)、 $\frac{7 x - 6}{2 x + 3} > 2$

查看试题解析
26. 解不等式组
${\begin{matrix} \begin{matrix} 9 x - 3 > x + 8 \\ - 3 x + 40 > x + 12 \\ \frac{x}{2} - 1 < \frac{x}{3} \end{matrix} \\ \frac{2 x - 3}{3} > 1 \end{matrix}$

查看试题解析
27. 解关于x的不等式
2mx+3<3x+n．

查看试题解析

四、解答题

28. 北京奥运会期间，某旅行社组团去北京观看某场足球比赛，入住某宾馆．已知该宾馆一楼房间比二楼房间少5间，该旅游团有48人，若全部安排在一楼，每间住4人，房间不够，每间住5人，有房间没住满．若全部安排在二楼，每间住3人，房间不够，每间住4人，则有房间没住满．你能根据以上信息确定宾馆一楼有多少房间吗？

查看试题解析
29. 已知a₁ ， a₂ ， a₃ ， a₄ ， a₅ ， a₆ ， a₇是彼此互不相等的正整数，它们的和等于159，求其中最小数a₁的最大值．

查看试题解析
30. 已知实数a是不等于3的常数，解不等式组 ${\begin{cases} - 2 x + 3 \geq - 3 \\ \frac{1}{2} x - 2 a + \frac{1}{2} x < 0 \end{cases}$ ，并依据a的取值情况写出其解集．

查看试题解析
31. 深化理解：
新定义：对非负实数x“四舍五入”到个位的值记为＜x＞，
即：当n为非负整数时，如果n﹣ $\frac{1}{2}$ ≤x＜n+ $\frac{1}{2}$ ，则＜x＞=n；
反之，当n为非负整数时，如果＜x＞=n，则n﹣ $\frac{1}{2}$ ≤x＜n+ $\frac{1}{2}$ ．
例如：＜0＞=＜0.48＞=0，＜0.64＞=＜1.49＞=1，＜2＞=2，＜3.5＞=＜4.12＞=4，…
试解决下列问题：

(1)、填空：①＜π＞=（π为圆周率）； ②如果＜x﹣1＞=3，则实数x的取值范围为．

(2)、若关于x的不等式组 ${\begin{matrix} \frac{2 x - 4}{3} \leq x - 1 \\ < a > - x > 0 \end{matrix}$ 的整数解恰有3个，求a的取值范围．

(3)、求满足＜x＞= $\frac{4}{3}$ x 的所有非负实数x的值．

查看试题解析
32. 十字形的路口，东西、南北方向的行人车辆来来往往，车水马龙．为了不让双方挤在一起，红绿灯就应动而生，一个方向先过，另一个方向再过．如在南稍门的十字路口，红灯绿灯的持续时间是不同的，红灯的时间总比绿灯长．即当东西方向的红灯亮时，南北方向的绿灯要经过若干秒后才亮．这样方可确保十字路口的交通安全．
那么，如何根据实际情况设置红绿灯的时间差呢？
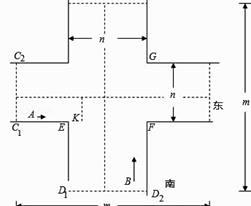
如图所示，假设十字路口是对称的，宽窄一致．设十字路口长为m米，宽为n米．当绿灯亮时最后一秒出来的骑车人A，不与另一方向绿灯亮时出来的机动车辆B相撞，即可保证交通安全．
根据调查，假设自行车速度为4m/s，机动车速度为8m/s．若红绿灯时间差为t秒．通过上述数据，请求出时间差t要满足什么条件时，才能使车人不相撞．当十字路口长约64米，宽约16米，路口实际时间差t=8s时，骑车人A与机动车B是否会发生交通事故？

查看试题解析
33. 某公司计划生产甲、乙两种产品共20件，其总产值w（万元）满足：1150<w<1200，相关数据如下表，为此，公司应怎样设计这两种产品的生产方案？

查看试题解析
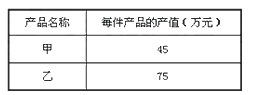34. 在车站开始检票时，有a（a＞0）各旅客在候车室排队等候检票进站，检票开始后，仍有旅客继续前来排队等候检票进站．设旅客按固定的速度增加，检票口检票的速度也是固定的，若开放一个检票口，则需30min才可将排队等候检票的旅客全部检票完毕；若开放两个检票口，则只需10min便可将排队等候检票的旅客全部检票完毕；现在要求在5min内将排队等候检票的旅客全部检票完毕，以使后来到站的旅客能随到随检，问至少要同时开放几个检票口？

查看试题解析
35. 若三角形的三边长分别是2、x、8，且x是不等式 $\frac{x + 2}{2}$ >- $\frac{1 - 2 x}{3}$ 的正整数解，试求第三边x的长．

查看试题解析
36. 已知a＜0，-1＜b＜0，试比较a、ab、ab²的大小．

查看试题解析
37. 解关于x的不等式组
${\begin{matrix} a x - 4 < 8 - 3 a x \\ (a + 2) x - 2 > 2 (1 - a) x + 4 \end{matrix}$

查看试题解析

五、综合题

38. 某机器人公司为扩大经营，决定购进 6 台机器用于生产某种小机器人．现有甲、乙两种机器供选择，其中每台机器的价格和日生产量如下表所示．经过预算，本次购买机器的费用不能超过 34 万元．

甲种机器

乙种机器

价格/（万元/台）

5

7

每台机器的日生产量/个

60

100

(1)、按要求该公司有几种购买方案？

(2)、若该公司购进的6台机器的日生产量不能少于380个，那么为了节约资金，应选择哪种购买方案？

查看试题解析
39.

(1)、①如果 a-b＜0，那么 ab；②如果 a-b=0，那么 ab；
③如果 a-b＞0，那么 ab；

(2)、由（1）你能归纳出比较a与b大小的方法吗？请用文字语言叙述出来．

(3)、用（1）的方法你能否比较3x²-3x+7与4x²-3x+7的大小？如果能，请写出比较过程．

查看试题解析
40. 学校为了奖励初三优秀毕业生，计划购买一批平板电脑和一批学习机，经投标，购买1台平板电脑3 000元，购买1台学习机800元.

(1)、学校根据实际情况，决定购买平板电脑和学习机共100台，要求购买的总费用不超过168 000元，则购买平板电脑最多多少台？

(2)、在(1)的条件下，购买学习机的台数不超过平板电脑台数的1.7倍.请问有哪几种购买方案？哪种方案最省钱？

查看试题解析
41. 现计划把甲种货物1240吨和乙种货物880吨用一列货车运往某地，已知这列货车挂在A、B两种不同规格的货车厢共40节，使用A型车厢每节费用为6000元，使用B型车厢每节费用为8000元.

(1)、设运送这批货物的总费用为y万元，这列货车挂A型车厢x 节，试定出用车厢节数x表示总费用y的公式.

(2)、如果每节A型车厢最多可装甲种货物35吨和乙种货物15吨，每节B型车厢最多可装甲种货物25吨和乙种货物35吨，装货时按此要求安排A、B两种车厢的节数，那么共有哪几种安排车厢的方案？

查看试题解析
42. “溱潼会船节”开幕式这天，某停车场预计停放的大小汽车共1200辆，该停车场的收费标准为：大车每车次10元，小车每车次为5元，根据预计，解答下列问题：

(1)、写出开幕式这天停车场的收费金额y（元）与小车停放数x（辆）之间的函数关系式，并指出自变量x的收费范围．

(2)、如果开幕式这天停放的小车辆占停车总车辆的65%至85%，请你估计开幕式这天该停车场收费金额的范围．

(3)、如果停车场预计收费总额不少于10000元，则至多停放多少辆小车？

查看试题解析
43. 在东营市中小学标准化建设工程中，某学校计划购进一批电脑和电子白板，经过市场考察得知，购买1台电脑和2台电子白板需要3.5万元，购买2台电脑和1台电子白板需要2.5万元．

(1)、求每台电脑、每台电子白板各多少万元？

(2)、根据学校实际，需购进电脑和电子白板共30台，总费用不超过30万元，但不低于28万元，请你通过计算求出有几种购买方案，哪种方案费用最低．

查看试题解析
44. 阅读材料：解分式不等式 $\frac{3 x + 6}{x - 1}$ ＜0
解：根据实数的除法法则：同号两数相除得正数，异号两数相除得负数，因此，原不等式可转化为：
① ${\begin{matrix} 3 x + 6 < 0 \\ x - 1 > 0 \end{matrix}$ 或② ${\begin{matrix} 3 x + 6 > 0 \\ x - 1 < 0 \end{matrix}$
解①得：无解，解②得：﹣2＜x＜1
所以原不等式的解集是﹣2＜x＜1
请仿照上述方法解下列分式不等式：

(1)、 $\frac{x - 4}{2 x + 5}$ ≤0

(2)、 $\frac{x + 2}{2 x - 6}$ ＞0．

查看试题解析
45. 某县筹备20周年县庆，园林部门决定利用3 490盆甲种花卉和2 950盆乙种花卉搭配A，B两种园艺造型共50个摆放在迎宾大道两侧，已知搭配一个A种造型需甲种花卉80盆，乙种花卉40盆；搭配一个B种造型需甲种花卉50盆，乙种花卉90盆.

(1)、某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计，问符合题意的搭配方案有几种?请你帮助设计出来；

(2)、若搭配一个A种造型的成本是800元，搭配一个B种造型的成本是960元，试说明(1)中哪种方案成本最低，最低成本是多少元?

查看试题解析
46. 已知不等式a<x≤b的整数解为5,6,7.

(1)、当a,b为整数时,求a,b的值;

(2)、当a,b为实数时,求a,b的取值范围.

查看试题解析
47. 对于三个数a、b、c，M（a，b，c）表示a、b、c这三个数的平均数，min{a，b，c}表示a、b、c这三个数中最小的数，如：M（﹣1，2，3）= $\frac{- 1 + 2 + 3}{3}$ = $\frac{4}{3}$ ，min{﹣1，2，3}=﹣1，M（﹣1，2，a）= $\frac{- 1 + 2 + a}{3}$ = $\frac{a + 1}{3}$ ，min{﹣1，2，a}= ${\begin{cases} a (a \leq - 1) \\ - 1 (a > - 1) \end{cases}$ ．
解决下列问题：

(1)、填空：若min{2，2x+2，4﹣2x}=2，则x的取值范围为；

(2)、①若M{2，x+1，2x}=min{2，x+1，2x}，那么x=；
②根据①，你发现了结论“若M{a，b，c}=min{a，b，c}，那么”（填a、b、c的大小关系）．
③运用②，填空：若M{2x+y+2，x+2y，2x﹣y}=min{2x+y+2，x+2y，+2x﹣y，则x+y ．

查看试题解析

	甲种机器	乙种机器
价格/（万元/台）	5	7
每台机器的日生产量/个	60	100