湘教版备考2021年中考数学三轮复习专题1数与式

试卷更新日期：2021-05-12 类型：三轮冲刺

进入出卷网下载

一、单选题

1. 下列说法中，正确的是（）

A、若a≠b，则a²≠b² B、若a＞|b|，则a＞b C、若|a|=|b|，则a=b D、若|a|＞|b|，则a＞b

查看试题解析
2. 实数a，b，c，d在数轴上的对应点的位置如图所示，则正确的结论是（）

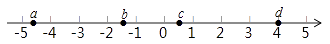A、a>–4 B、bd>0 C、|a|>|d| D、b+c>0

查看试题解析
3. 设a= $\sqrt{1003} + \sqrt{997}$ ，b= $\sqrt{1001} + \sqrt{999}$ ，c= $2 \sqrt{1000}$ ，则a，b，c之间的大小关系是（）

A、a<b<c B、c<b<a C、c<a<b D、a<c<b

查看试题解析
4. 如图，直线l：y＝x+1交y轴于点A₁ ，在x轴正方向上取点B₁ ，使OB₁＝OA₁；过点B₁作A₂B₁⊥x轴，交l于点A₂ ，在x轴正方向上取点B₂ ，使B₁B₂＝B₁A₂；过点B₂作A₃B₂⊥x轴，交l于点A₃ ，在x轴正方向上取点B₃ ，使B₂B₃＝B₂A₃；…记△OA₁B₁面积为S₁ ， △B₁A₂B₂面积为S₂ ， △B₂A₃B₃面积为S₃ ， …则S₂₀₁₇等于（）

A、2⁴⁰³⁰ B、2⁴⁰³¹ C、2⁴⁰³² D、2⁴⁰³³

查看试题解析
5. 若 $x > 1$ ， $y > 0$ ，且满足 $x y = x^{y} ， \frac{x}{y} = x^{3 y}$ ，则 $x + y$ 的值为（）.

A、1 B、2 C、 $\frac{9}{2}$ D、 $\frac{11}{2}$

查看试题解析
6. 在矩形ABCD内，将两张边长分别为a和b(a>b)的正方形纸片按图1，图2两种方式放置(图1，图2中两张正方形纸片均有部分重叠)，矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图2中阴影部分的周长与图1中阴影部分的周长的差为l，若要知道l的值，只要测量图中哪条线段的长（）

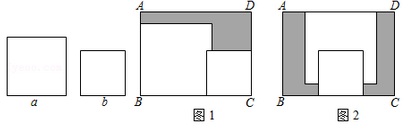A、a B、b C、AD D、AB

查看试题解析
7. 一个大正方形内放入两个同样大小的小正方形纸片，按如图1放置，两个小正方形纸片的重叠部分面积为4；按如图2放置（其中一小张正方形居大正方形的正中），大正方形中没有被小正方形覆盖的部分（阴影部分）的面积为44，则把两张小正方形按如图3放置时，两个小正方形重叠部分的面积为（）

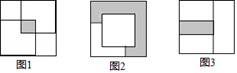A、10 B、12 C、14 D、16

查看试题解析
8. n是整数，式子 $\frac{1}{8}$ [1﹣（﹣1）ⁿ]（n²﹣1）计算的结果（　　）

A、是0 B、总是奇数 C、总是偶数 D、可能是奇数也可能是偶数

查看试题解析
9. 如果 $a$ ， $b$ ， $c$ 是正数，且满足 $a + b + c = 1$ ， $\frac{1}{a + b} + \frac{1}{b + c} + \frac{1}{a + c} = 5$ ，那么 $\frac{c}{a + b} + \frac{a}{b + c} + \frac{b}{a + c}$ 的值为（）

A、-1 B、1 C、2 D、 $\frac{1}{2}$

查看试题解析
10. 当x分别取﹣2015、﹣2014、﹣2013、…，、﹣2、﹣1、0、1、 $\frac{1}{2}$ 、 $\frac{1}{3}$ 、…、 $\frac{1}{2013}$ 、 $\frac{1}{2014}$ 、 $\frac{1}{2015}$ 时，计算分式 $\frac{x^{2} - 1}{x^{2} + 1}$ 的值，再将所得结果相加，其和等于（）

A、﹣1 B、1 C、0 D、2015

查看试题解析
11. 如果最简根式 $\sqrt{3 a - 8}$ 与 $\sqrt{17 - 2 a}$ 是同类二次根式，那么使 $\sqrt{4 a - 2 x}$ 有意义的x的取值范围是（　　）

A、x≤10 B、x≥10 C、x＜10 D、x＞10　

查看试题解析
12. 已知x为实数，化简 $\sqrt{- x^{3}} - x \sqrt{- \frac{1}{x}}$ 的结果为（　　）

A、 $(x - 1) \sqrt{- x}$ B、 $(- 1 - x) \sqrt{- x}$ C、 $(1 - x) \sqrt{- x}$ D、 $(1 + x) \sqrt{- x}$

查看试题解析
13. 对于任意的正数m、n定义运算※为：m※n= $\{\begin{matrix} \sqrt{m} - \sqrt{n} (m \geq n) \\ \sqrt{m} + \sqrt{n} (m < n) \end{matrix}$ ，计算（3※2）×（8※12）的结果为（　　）

A、2﹣4 $\sqrt{6}$ B、2 C、2 $\sqrt{5}$ D、20

查看试题解析

二、填空题

14. 对于正整数n定义阶乘 $n! = 1 \times 2 \times 3 \times \dots \times （ n - 1 ） \times n$ ，则 $1 \times 1! + 2 \times 2! + 3 \times 3! + \dots + 100 \times 100! =$ （用阶乘表示）

查看试题解析
15. 若a是一个完全平方数，则比a大的最小完全平方数是。

查看试题解析
16. 从﹣1，0，2，3四个数中任取两个不同的数（记作a_k ， b_k）构成一个数对M_k＝{a_k ， b_k）（其中k＝1，2，…，s ，且将{a_k ， b_k}与{b_k ， a_k}视为同一个数对），若满足：对于任意的M_i＝{a_i ， b_i}和M_j＝{a_j ， b_j）（i≠j ， 1≤i≤s ， 1≤j≤s）都有a_i+b_i≠a_j+b_j ，则s的最大值是．

查看试题解析
17. 使得m²+m+7是完全平方数的所有整数m的积是。

查看试题解析
18. 分解因式（xy﹣1）²﹣（x+y﹣2xy）（2﹣x﹣y）= ．

查看试题解析
19. 观察下列各式： $\frac{2}{1 \times 3}$ = $\frac{1}{1}$ ﹣ $\frac{1}{3}$ ；
$\frac{2}{2 \times 4}$ = $\frac{1}{2}$ ﹣ $\frac{1}{4}$ ；

$\frac{2}{3 \times 5}$ = $\frac{1}{3}$ ﹣ $\frac{1}{5}$ ；

…

请利用你所得结论，化简代数式： $\frac{1}{1 \times 3}$ + $\frac{1}{2 \times 4}$ + $\frac{1}{3 \times 5}$ +…+ $\frac{1}{n (n + 2)}$ （n≥3且n为整数），其结果为．

查看试题解析
20. 若实数 $a = \frac{1}{2 - \sqrt{3}}$ ，则代数式 $a^{2} - 4 a + 4$ 的值为.

查看试题解析
21. 观察下面的变化规律：
$\frac{2}{1 \times 3} = 1 - \frac{1}{3} ， \frac{2}{3 \times 5} = \frac{1}{3} - \frac{1}{5} ， \frac{2}{5 \times 7} = \frac{1}{5} - \frac{1}{7} ， \frac{2}{7 \times 9} = \frac{1}{7} - \frac{1}{9}$ ，……

根据上面的规律计算：

$\frac{2}{1 \times 3} + \frac{2}{3 \times 5} + \frac{2}{5 \times 7} + \dots + \frac{2}{2019 \times 2021} =$ ．

查看试题解析
22. 刘莎同学用火柴棒依图的规律摆六边形图案，用10086根火柴棒摆出的图案应该是第个．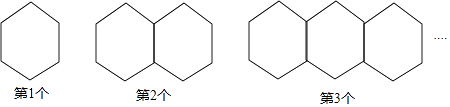

查看试题解析

三、计算题

23. 请先阅读下列一段内容，然后解答问题：
因为： $\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ， $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ， $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ，…… ， $\frac{1}{9 \times 10} = \frac{1}{9} - \frac{1}{10}$ ，

所以： $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{9 \times 10}$

$= (1 - \frac{1}{2}) + (\frac{1}{2} - \frac{1}{3}) + (\frac{1}{3} - \frac{1}{4}) + \dots + (\frac{1}{9} - \frac{1}{10})$

$= 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \dots + \frac{1}{9} - \frac{1}{10} = 1 - \frac{1}{10} = \frac{9}{10}$

计算：

(1)、 $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{2007 \times 2008}$ ；

(2)、 $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} + \dots + \frac{1}{49 \times 51}$ .

查看试题解析
24. 计算：

(1)、 $(- 56) \times (\frac{4}{7} - \frac{3}{8} + \frac{1}{14})$

(2)、 $2 \times {(- 3)}^{2} - 5 \div (- \frac{1}{2}) \times (- 2)$

(3)、有个填写运算符号的游戏:在“ $1 □ 2 □ 6 □ 9$ ”中的每个口内，填入 $+, -, \times, \div$ 中的某一个(可重复使用)，然后计算结果
①算: $1 + 2 - 6 - 9$ .

② $1 \div 2 \times 6 □ 9 = - 6$ ，请在 $□$ 内直接填出运算符号.

③“ $1 □ 2 □ 6 - 9$ ”中的口内填入符号后，使计算所得数最小，请在口内直接填出运算符号.

查看试题解析
25. 课堂上老师讲解了比较 $\sqrt{11} - \sqrt{10}$ 和 $\sqrt{15} - \sqrt{14}$ 的方法，观察发现11-10＝15-14＝1，于是比较这两个数的倒数：
$\frac{1}{\sqrt{11} - \sqrt{10}} = \frac{\sqrt{11} + \sqrt{10}}{(\sqrt{11} - \sqrt{10}) (\sqrt{11} + \sqrt{10)}} = \sqrt{11} + \sqrt{10}$

$\frac{1}{\sqrt{15} - \sqrt{14}} = \frac{\sqrt{15} + \sqrt{14}}{(\sqrt{15} - \sqrt{14}) (\sqrt{15} + \sqrt{14)}} = \sqrt{15} + \sqrt{14}$

因为 $\sqrt{15} + \sqrt{14} > \sqrt{11} + \sqrt{10}$ ，所以 $\frac{1}{\sqrt{15} - \sqrt{14}} > \frac{1}{\sqrt{11} - \sqrt{10}}$ ，则有 $\sqrt{15} - \sqrt{14} < \sqrt{11} - \sqrt{10}$ ，

请你设计一种方法比较 $\sqrt{8} + \sqrt{3}$ 与 $\sqrt{6} + \sqrt{5}$ 的大小，

查看试题解析
26. 如果我们要计算1+2+2²+2³+……+*2⁹⁹+2¹⁰⁰的值，我们可以用如下的方法：
解：设S=1+2+2²+2³+……+2⁹⁹+2¹⁰⁰①式

在等式两边同乘以2，则有2S=2+2²+2³+……+2⁹⁹+2¹⁰⁰+2¹⁰¹②式

②式减去①式，得2S-S=2¹⁰¹-1

即S=2¹⁰¹-1

即1+2+2²+2³+……+2⁹⁹+2¹⁰⁰=2¹⁰¹-1

[理解运用]计算：

(1)、1+3+3²+3³+……+3⁹⁹+3¹⁰⁰；

(2)、1-3+3²-3³+……-3⁹⁹+3¹⁰⁰

查看试题解析
27. 计算： $(2 + 1) (2^{2} + 1) (2^{4} + 1) (2^{8} + 1) (2^{16} + 1) (2^{32} + 1) + 1$ 的结果.

查看试题解析
28. 请先阅读下列文字与例题,再回答后面的问题:
当因式分解中,无法直接运用提取公因式和乘法公式时,我们往往可以尝试一个多项式分组后,再运用提取公因式或乘法公式继续分解的方法是分组分解法.

例如:

① $a m + a n + b m + b n$

= $(a m + a n) + (b m + b n)$

= $a (m + n) + b (m + n)$

= $(m + n) (a + b)$

② $x^{2} - y^{2} - 2 y - 1$

= $x^{2} - (y^{2} + 2 y + 1)$

= $x^{2} - {(y + 1)}^{2}$

= $(x + y + 1) (x - y - 1)$

(1)、根据上面的知识,我们可以将下列多项式进行因式分解:
$a x - a y - b x + b y =$ ()-()=()();

$x^{2} - y^{2} + x - y$ =()+()=()().

(2)、分解下列因式:
① $a b - a c + b - c$ ;

② $- 4 b^{2} + 9 a^{2} - 6 a c + c^{2}$ .

查看试题解析
29. 计算 $\frac{1}{x (x + 1)} + \frac{1}{(x + 1) (x + 2)} + \frac{1}{(x + 2) (x + 3)} + \dots + \frac{1}{(x + 2017) (x + 2018)}$ 并求当x=1时,该代数式的值.

查看试题解析
30. 若x ， y为实数，且y＝ $\sqrt{1 - 4 x}$ ＋ $\sqrt{4 x - 1}$ ＋ $\frac{1}{2}$ ．求 $\sqrt{\frac{x}{y} + 2 + \frac{y}{x}}$ － $\sqrt{\frac{x}{y} - 2 + \frac{y}{x}}$ 的值．

查看试题解析

四、解答题

31. 某商场在世界杯足球比赛期间举行促销活动，并设计了两种方案：一种是以商品价格的九五折优惠的方式进行销售；一种是采用有奖销售的方式，具体措施是：①有奖销售自2009年6月9日起，发行奖券10000张，发完为止；②顾客累计购物满400元，赠送奖券一张（假设每位顾客购物每次都恰好凑足400元）；③世界杯后，顾客持奖券参加抽奖；④奖项是：特等奖2名，各奖3000元奖品；一等奖10名，各奖1000元奖品；二等奖20名，各奖300元奖品；三等奖100名，各奖100元奖品；四等奖200名，各奖50元奖品；纪念奖5000名，各奖10元奖品，试就商场的收益而言，对两种促销方法进行评价，选用哪一种更为合算？

查看试题解析
32. 已知三个互不相等的有理数，既可以表示为1，a，a+b的形式，又可以表示0， $\frac{b}{a}$ ，b的形式，试求a^2n-1a²ⁿ（n≥1）的值.

查看试题解析
33. 某电器商销售一种微波炉和电磁炉，微波炉每台定价800元，电磁炉每台定价200元．“双十一”期间商场决定开展促销活动，活动期间向客户提供两种优惠方案．
方案一：买一台微波炉送一台电磁炉；方案二：微波炉和电磁炉都按定价的90%付款．

现某客户要到该卖场购买微波炉2台，电磁炉x台（x＞2）．

(1)、若该客户按方案一购买，需付款元．（用含x的代数式表示）；若该客户按方案二购买，需付款元．（用含x的代数式表示）

(2)、若x＝5时，通过计算说明此时按哪种方案购买较为合算？

(3)、当x＝5时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法．

查看试题解析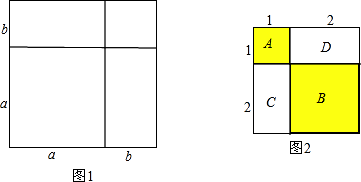
34. 问题再现：
数形结合是解决数学问题的一种重要的思想方法，借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性，从而可以帮助我们快速解题．初中数学里的一些代数公式，很多都可以通过表示几何图形面积的方法进行直观推导和解释．
例如：利用图形的几何意义证明完全平方公式．
证明：将一个边长为a的正方形的边长增加b，形成两个矩形和两个正方形，如图1：
这个图形的面积可以表示成：
（a+b）²或 a²+2ab+b²
∴（a+b）²=a²+2ab+b²
这就验证了两数和的完全平方公式．
类比解决：
①请你类比上述方法，利用图形的几何意义证明平方差公式．（要求画出图形并写出推理过程）
问题提出：如何利用图形几何意义的方法证明：1³+2³=3²？
如图2，A表示1个1×1的正方形，即：1×1×1=1³
B表示1个2×2的正方形，C与D恰好可以拼成1个2×2的正方形，因此：B、C、D就可以表示2个2×2的正方形，即：2×2×2=2³
而A、B、C、D恰好可以拼成一个（1+2）×（1+2）的大正方形．
由此可得：1³+2³=（1+2）²=3²
尝试解决：
②请你类比上述推导过程，利用图形的几何意义确定：1³+2³+3³= ▲ ．（要求写出结论并构造图形写出推证过程）．
问题拓广：
③请用上面的表示几何图形面积的方法探究：1³+2³+3³+…+n³= ▲ ．（直接写出结论即可，不必写出解题过程）

查看试题解析
35. 用平方差公式进行因式分解在数的运算中有着广泛的应用，比如，数的整除性探究中的应用．
例： $2008^{3} - 2008$ 能被2009整除吗？

解: $2008^{3} - 2008 = 2008 (2008^{2} - 1) = 2008 (2008 + 1) (2008 - 1) = 2008 \times 2009 \times 2007$

∵ $2008^{3} - 2008$ 中有因数2009，

∴ $2008^{3} - 2008$ 一定能被2009整除．

请你试一试：已知数字 $(2^{48} - 1)$ 恰能被两个在60和70之间的整数整除，求出这两个数．

查看试题解析
36.
已知，求a的值．

查看试题解析

五、综合题

37. 阅读下列材料：小明为了计算 $1 + 2 + 2^{2} + \dots + 2^{2017} + 2^{2018}$ 的值，采用以下方法：
设 $S = 1 + 2 + 2^{2} + \dots + 2^{2017} + 2^{2018}$ ①

则 $2 S = 2 + 2^{2} + \dots + 2^{2018} + 2^{2019}$ ②

②-①得 $2 S - S = 2^{2019} - 1$

∴ $S = 1 + 2 + 2^{2} + \dots + 2^{2017} + 2^{2018} = 2^{2019} - 1$

(1)、 $1 + 2 + 2^{2} + \dots + 2^{9}$ = ；

(2)、 $3 + 3^{2} + \dots + 3^{10}$ = ；

(3)、求1+a+a²+.....+aⁿ的和（ $a > 0$ ， $n$ 是正整数，请写出计算过程）.

查看试题解析
38. 任意无理数都是由整数部分和小数部分构成的.
已知一个无理数 $a$ ，它的整数部分是 $b$ ，则它的小数部分可以表示为 $a - b$ .例如：

$\sqrt{4} < \sqrt{6} < \sqrt{9}$ ，即 $2 < \sqrt{6} < 3$ ，显然 $\sqrt{6}$ 的整数部分是2，小数部分是 $\sqrt{6} - 2$ .

根据上面的材料，解决下列问题：

(1)、若 $\sqrt{11}$ 的整数部分是 $m$ ， $\sqrt{5}$ 的整数部分是 $n$ ，求 $\sqrt{5} - \sqrt{m + n}$ 的值.

(2)、若 $7 + \sqrt{14}$ 的整数部分是 $2 x$ ，小数部分是 $y$ ，求 $\frac{x}{2} - y + \sqrt{14}$ 的值.

查看试题解析
39. 我们知道，任意一个正整数x都可以进行这样的分解：x=m×n（m，n是正整数，且m≤n），在x的所有这种分解中，如果m，n两因数之差的绝对值最小，我们就称m×n是x的最佳分解．并规定：f（x）= $\frac{m}{n}$ .
例如：18可以分解成1×18，2×9或3×6，因为18-1>9-2>6-3，所以3×6是18的最佳分解，所以f（18）= $\frac{3}{6}$ = $\frac{1}{2}$ ．

(1)、填空：f（6）= ， f（9）=；

(2)、一个两位正整数t（t=10a+b，1≤a≤b≤9，a，b为正整数），交换其个位上的数字与十位上的数字，得到的新数减去原数所得的差为54，求出所有满足条件的两位正整数，并求f（t）的最大值．

查看试题解析
40. 材料：
数学兴趣一小组的同学对完全平方公式进行研究：因 ${(a - b)}^{2} \geq 0$ ，将左边展开得到 $a^{2} - 2 a b + b^{2} \geq 0$ ，移项可得 $a^{2} + b^{2} \geq 2 a b$ .（当且仅当 $a = b$ 时，取“ $=$ ”）

数学兴趣二小组受兴趣一小组的启示，继续研究发现：对于任意两个非负数 $m$ ， $n$ ，都存在 $m + n \geq 2 \sqrt{m n}$ （当且仅当 $m = n$ 时，取“ $=$ ”）并进一步发现，两个非负数 $m$ ， $n$ 的和一定存在着个最小值.

根据材料，解答下列问题：

(1)、 ${(3 x)}^{2} + {(4 y)}^{2} \geq$ （ $x > 0$ ， $y > 0$ ）； $x^{2} + {(\frac{1}{x})}^{2} \geq$ （ $x > 0$ ）；

(2)、求 $12 x + \frac{3}{4 x} (x > 0)$ 的最小值；

(3)、已知 $x > 2$ ，当 $x$ 为何值时，代数式 $3 x + \frac{4}{3 x - 6} + 2010$ 有最小值？并求出这个最小值.

查看试题解析
41. 阅读与思考
x²+（p+q）x+pq型式子的因式分解

x²+（p+q）x+pq型式子是数学学习中常见的一类多项式，如何将这种类型的式子分解因式呢？

我们通过学习，利用多项式的乘法法则可知：（x+p）（x+q）＝x²+（p+q）x+pq，因式分解是整式乘法相反方向的变形，利用这种关系可得x²+（p+q）x+pq＝（x+p）（x+q）.

利用这个结果可以将某些二次项系数是1的二次三项式分解因式，例如，将x²﹣x﹣6分解因式.这个式子的二次项系数是1，常数项﹣6＝2×（﹣3），一次项系数﹣1＝2+（﹣3），因此这是一个x²+（p+q）x+pq型的式子.所以x²﹣x﹣6＝（x+2）（x﹣3）.

上述过程可用十字相乘的形式形象地表示：先分解二次项系数，分别写在十字交叉线的左上角和左下角；再分解常数项，分别写在十字交叉线的右上角和右下角；然后交叉相乘，求代数和，使其等于一次项系数，如图所示.

这样我们也可以得到x²﹣x﹣6＝（x+2）（x﹣3）.这种分解二次三项式的方法叫“十字相乘法”.

请同学们认真观察，分析理解后，解答下列问题：

(1)、分解因式：y²﹣2y﹣24.

(2)、若x²+mx﹣12（m为常数）可分解为两个一次因式的积，请直接写出整数m的所有可能值.

查看试题解析
42. 我们知道，假分数可以化为整数与真分数的和的形式，例如： $\frac{3}{2} = 1 + \frac{1}{2}$ ，在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为“假分式”；当分子的次数小于分母的次数时，我们称之为“真分式”．
例如： $\frac{x + 1}{x - 2}$ ， $\frac{x^{2}}{x + 2} \cdot \cdot \cdot \cdot \cdot$ 像这样的分式是假分式；像 $\frac{1}{x - 2}$ ， $\frac{x}{x^{2} - 1} \cdot \cdot \cdot \cdot \cdot$ 这样的分式是真分式，类似的，假分式也可以化为整式与真分式的和的形式．例如： $\frac{x + 1}{x - 2} = \frac{(x - 2) + 3}{x - 2} = 1 + \frac{3}{x - 2}$ ； $\frac{x^{2}}{x + 2} = \frac{(x + 2) (x - 2) + 4}{x + 2} = x - 2 + \frac{4}{x + 2}$ ，解决下列问题：

(1)、将分式 $\frac{x - 2}{x + 3}$ 化为整式与真分式的和的形式为：（直接写出结果即可）

(2)、如果分式 $\frac{x^{2} + 2 x}{x + 3}$ 的值为整数，求 $x$ 的整数值

查看试题解析
43. 阅读材料，回答问题：
两个含有二次根式的代数式相乘，如果它们的积不含有二次根式，我们就说这两个代数式互为有理化因式.例如：因为 $\sqrt{a} \times \sqrt{a} = a$ ， $(\sqrt{2} + 1) (\sqrt{2} - 1) = 1$ ，所以 $\sqrt{a}$ 与 $\sqrt{a}$ ， $\sqrt{2} + 1$ 与 $\sqrt{2} - 1$ 互为有理化因式.

(1)、 $2 \sqrt{3} - 1$ 的有理化因式是；

(2)、这样，化简一个分母含有二次根式的式子时，采用分子、分母同乘以分母的有理化因式的方法就可以了，例如： $\frac{2}{\sqrt{3}} = \frac{2 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{2 \sqrt{3}}{3}$ ，
$\frac{\sqrt{5} + \sqrt{3}}{\sqrt{5} - \sqrt{3}} = \frac{{(\sqrt{5} + \sqrt{3})}^{2}}{(\sqrt{5} - \sqrt{3}) (\sqrt{5} + \sqrt{3})} = \frac{5 + 2 \sqrt{15} + 3}{5 - 3} = \frac{8 + 2 \sqrt{15}}{2} = 4 + \sqrt{15}$

用上述方法对 $\frac{2 - \sqrt{3}}{2 + \sqrt{3}}$ 进行分母有理化.

(3)、若 $a = \frac{1}{2 + \sqrt{5}}$ ， $b = 2 - \sqrt{5}$ ，判断 $a$ 与 $b$ 的关系并说明理由.

(4)、直接写结果： $(\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \dots + \frac{1}{\sqrt{2020} + \sqrt{2019}}) (\sqrt{2020} + 1) =$ .

查看试题解析