广东省肇庆市2021届高三下学期数学第三次统一检测试卷
试卷更新日期:2021-05-12 类型:高考模拟
一、单选题
-
1. 已知复数 ,则复数 的虚部为( )A、2 B、-2 C、 D、2. 已知 ,则( )A、 B、 C、 D、3. ,则 ( )A、49 B、56 C、59 D、644. 中国南北朝时期数学家、天文学家祖冲之、祖暅父子总结了魏晋时期著名数学家刘徽的有关工作,提出“幂势既同,则积不容异”.“幂”是截面积,“势”是几何体的高.详细点说就是,界于两个平行平面之间的两个几何体,被任一平行于这两个平面的平面所截,如果两个截面的面积相等,则这两个几何体的体积相等.上述原理在中国被称为祖暅原理.一个上底面边长为1,下底面边长为2,高为 的正六棱台与一个不规则几何体满足“幂势既同”,则该不规则几何体的体积为( )
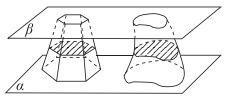 A、16 B、 C、 D、215. 函数 的部分图象大致为( )A、
A、16 B、 C、 D、215. 函数 的部分图象大致为( )A、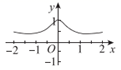 B、
B、 C、
C、 D、
D、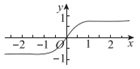 6. 在 的等腰直角 中, 为 的中点, 为 的中点, ,则 ( )A、 B、 C、 D、-17. 已知 是椭圆 的右焦点,过椭圆 的下顶点且斜率为 的直线与以点 为圆心、半焦距为半径的圆相切,则椭圆 的离心率为( )A、 B、 C、 D、8. 已知函数 有三个零点,则实数 的取值范围是( )A、 B、 C、 D、
6. 在 的等腰直角 中, 为 的中点, 为 的中点, ,则 ( )A、 B、 C、 D、-17. 已知 是椭圆 的右焦点,过椭圆 的下顶点且斜率为 的直线与以点 为圆心、半焦距为半径的圆相切,则椭圆 的离心率为( )A、 B、 C、 D、8. 已知函数 有三个零点,则实数 的取值范围是( )A、 B、 C、 D、二、多选题
-
9. 某学校组织学生参加劳动实践,学生需要手工制作一种模具,劳动实践结束后,学校任选了一个班级,统计了该班每人制作的合格品个数,其结果用茎叶图记录如下:

由以上统计结果,下列判断正确的是( )
A、男生制作合格品个数的方差更大 B、女生制作合格品个数的分布更接近正态分布. C、男生制作合格品个数的分布更接近正态分布 D、该班女生制作合格模具的平均能力要低于男生10. 已知集合 , ,则下列命题中正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 或 D、若 时,则 或11. 已知函数 ,则( )A、 B、 的最大值为 C、 是奇函数 D、 的最小值为12. 已知 是数列 的前 项和,且 , ,则( )A、数列 是等比数列 B、 恒成立 C、 恒成立 D、 恒成立三、填空题
-
13. 已知 , 分别是双曲线 的左、右焦点,点 是双曲线 上一点,且 , 的面积为 ,则双曲线 的渐近线方程为.14. 现有5个参加演讲比赛的名额,要分配给甲、乙、丙三个班级,要求每班至少要分配一个名额,则甲班恰好分配到两个名额的概率为.15. 在三棱锥 中, 是以 为直角的等腰直角三角形, 是边长为2的等边三角形,二面角 的余弦值为 ,则三棱锥 的外接球的表面积为.16. 写出一个以 为对称中心的偶函数 , 该函数的最小正周期是.
四、解答题
-
17. 如图,在平面四边形 中, , , , .
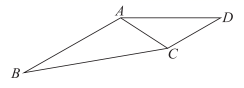 (1)、求 的值;(2)、求BC 的值.18. 已知:数列 中, , , , .(1)、证明数列 为等比数列,并求数列 的通项公式;(2)、若 ,求数列 的前 项和 .19. 如图,三棱柱 中, , , , 分别是 和 的中点,点 在棱 上,且 .
(1)、求 的值;(2)、求BC 的值.18. 已知:数列 中, , , , .(1)、证明数列 为等比数列,并求数列 的通项公式;(2)、若 ,求数列 的前 项和 .19. 如图,三棱柱 中, , , , 分别是 和 的中点,点 在棱 上,且 . (1)、证明: 平面 ;(2)、若 底面 , ,求二面角 的余弦值.20. 某高三学生小明准备利用暑假的7月和8月勤工俭学,现有“送外卖员”和“销售员”两份工作可供其选择.已知“销售员”工作每日底薪为50元,每日销售的前5件每件奖励20元,超过5件的部分每件奖励30元.小明通过调查,统计了100名销售员1天的销售记录,其柱状图如图1;“送外卖员”没有底薪,收入与送的单数相关,在一日内:1至20单(含20单)每送一单3元,超过20单且不超过40单的部分每送一单4元,超过40单的部分,每送一单4.5元.小明通过随机调查,统计了100名送外卖员的日送单数,并绘制成如下直方图(如图2).
(1)、证明: 平面 ;(2)、若 底面 , ,求二面角 的余弦值.20. 某高三学生小明准备利用暑假的7月和8月勤工俭学,现有“送外卖员”和“销售员”两份工作可供其选择.已知“销售员”工作每日底薪为50元,每日销售的前5件每件奖励20元,超过5件的部分每件奖励30元.小明通过调查,统计了100名销售员1天的销售记录,其柱状图如图1;“送外卖员”没有底薪,收入与送的单数相关,在一日内:1至20单(含20单)每送一单3元,超过20单且不超过40单的部分每送一单4元,超过40单的部分,每送一单4.5元.小明通过随机调查,统计了100名送外卖员的日送单数,并绘制成如下直方图(如图2).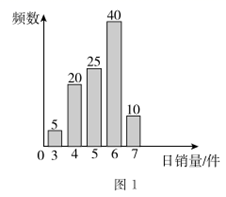
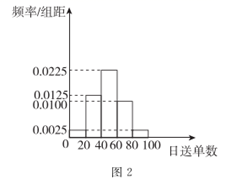 (1)、分别求出“销售员”的日薪 (单位:元)与销售件数 的函数关系式、“送外卖员”的日薪 (单位:元)与所送单数 的函数关系式;(2)、若将频率视为概率,根据统计图,试分别估计“销售员”的日薪 和“送外卖员”的日薪 (同一组中的数据用该组区间的中点值代表)的数学期望,分析选择哪种工作比较合适,并说明你的理由.
(1)、分别求出“销售员”的日薪 (单位:元)与销售件数 的函数关系式、“送外卖员”的日薪 (单位:元)与所送单数 的函数关系式;(2)、若将频率视为概率,根据统计图,试分别估计“销售员”的日薪 和“送外卖员”的日薪 (同一组中的数据用该组区间的中点值代表)的数学期望,分析选择哪种工作比较合适,并说明你的理由.