浙江省绍兴市2021年数学中考一模试卷
试卷更新日期:2021-05-11 类型:中考模拟
一、单选题
-
1. 如图是由5个相同的小正方体和1个圆锥组成的立体图形,这个立体图形的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 已知在 中, , , ,则 的长为( )A、 B、 C、 D、3. 已知 是锐角三角形,若 ,则( )A、 B、 C、 D、4. 如图,点B在⊙A上,点C在⊙A外,以下条件不能判定BC是⊙A切线的是( )
2. 已知在 中, , , ,则 的长为( )A、 B、 C、 D、3. 已知 是锐角三角形,若 ,则( )A、 B、 C、 D、4. 如图,点B在⊙A上,点C在⊙A外,以下条件不能判定BC是⊙A切线的是( )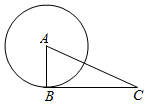 A、∠A=50°,∠C=40° B、∠B﹣∠C=∠A C、AB2+BC2=AC2 D、⊙A与AC的交点是AC中点5. 如图,这个圆锥的主(正)视图是一个边长为4的等边三角形,则这个圆锥的俯视图的面积为( )
A、∠A=50°,∠C=40° B、∠B﹣∠C=∠A C、AB2+BC2=AC2 D、⊙A与AC的交点是AC中点5. 如图,这个圆锥的主(正)视图是一个边长为4的等边三角形,则这个圆锥的俯视图的面积为( ) A、 B、 C、 D、6. 设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h、r、R,则下列结论不正确的是( )
A、 B、 C、 D、6. 设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h、r、R,则下列结论不正确的是( )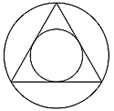 A、 B、 C、 D、7. 由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,则以下说法正确的是( )
A、 B、 C、 D、7. 由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,则以下说法正确的是( ) A、x=1或2,y=3 B、x=1或2,y=1或3 C、x=1,y=1或3 D、x=2,y=1或38. 如图,在边长相同的小正方形组成的网格中,点 都在这些小正方形的顶点上, 相交于点P,则 ( ).
A、x=1或2,y=3 B、x=1或2,y=1或3 C、x=1,y=1或3 D、x=2,y=1或38. 如图,在边长相同的小正方形组成的网格中,点 都在这些小正方形的顶点上, 相交于点P,则 ( ).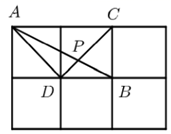 A、 B、3 C、 D、29. 如图,在矩形ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则sin∠CBE=( )
A、 B、3 C、 D、29. 如图,在矩形ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则sin∠CBE=( ) A、 B、 C、 D、10. 已知在 中, , 是 的中点, 的延长线上的点 满足 . 的内切圆与边 , 的切点分别为 , ,延长 分别与 , 的延长线交于 , ,则 ( )A、0.5 B、1 C、1.5 D、2
A、 B、 C、 D、10. 已知在 中, , 是 的中点, 的延长线上的点 满足 . 的内切圆与边 , 的切点分别为 , ,延长 分别与 , 的延长线交于 , ,则 ( )A、0.5 B、1 C、1.5 D、2二、填空题
-
11. 如图,有一个小山坡 ,坡比 .已知小山坡的水平距离 ,则小山坡的高度 是.
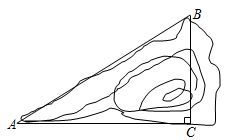 12. 圆的直径是 ,如果圆心与直线的距离是 ,那么该直线和圆的位置关系是.13. 如图1,一个圆球放置在 形架中,图2是它的平面示意图, 和 都是 的切线,切点分别是 ,若 的半径为 ,且 ,则 .
12. 圆的直径是 ,如果圆心与直线的距离是 ,那么该直线和圆的位置关系是.13. 如图1,一个圆球放置在 形架中,图2是它的平面示意图, 和 都是 的切线,切点分别是 ,若 的半径为 ,且 ,则 .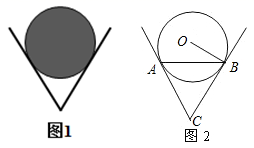 14. 同一平面内有 , , 三点, , 两点之间的距离为 ,点 到直线 的距离为 ,且 为直角三角形,则满足上述条件的点 有个.15. 如图,在 中, 交 , 于点 , , 与 的内切圆相切.若 的周长为12,则 的最大值为.
14. 同一平面内有 , , 三点, , 两点之间的距离为 ,点 到直线 的距离为 ,且 为直角三角形,则满足上述条件的点 有个.15. 如图,在 中, 交 , 于点 , , 与 的内切圆相切.若 的周长为12,则 的最大值为. 16. 如图,直线 : 与 轴交于点 ,与 轴交于点 ,以 为直径的 交 于另一点 ,把弧 沿直线 翻转后与 交于点 .
16. 如图,直线 : 与 轴交于点 ,与 轴交于点 ,以 为直径的 交 于另一点 ,把弧 沿直线 翻转后与 交于点 . (1)、当 时, ;(2)、若翻转后所得的弧与 相切,则此时 的值为.
(1)、当 时, ;(2)、若翻转后所得的弧与 相切,则此时 的值为.三、解答题
-
17. 计算: .18. 如图,已知圆柱底面的直径 ,圆柱的高 ,在圆柱的侧面上,过点 , 嵌有一圈长度最短的金属丝.(1)、现将圆柱侧面沿 剪开,所得的圆柱侧面展开图是______.A、
 ;
B、
;
B、 ;
C、
;
C、 ;
D、
;
D、 (2)、求该长度最短的金属丝的长.
(2)、求该长度最短的金属丝的长. 19. 如图,以△ABC的边BC为直径的⊙O,交AB边于点D,D为AB的中点,DE⊥AC于点E.
19. 如图,以△ABC的边BC为直径的⊙O,交AB边于点D,D为AB的中点,DE⊥AC于点E. (1)、求证:AC=BC.(2)、求证:DE是⊙O的切线.20. 某校为检测师生体温,在校门安装了某型号的测温门,如图为该“测温门”截面示意图.身高1.6米的小聪做了如下实验:当他在地面M处时“测温门”开始显示额头温度,此时在额头B处测得A的仰角为30°;当他在地面N处时,“测温门”停止显示额头温度,此时在额头C处测得A的仰角为53°.如果测得小聪的有效测温区间MN的长度是0.98米,求测温门顶部A处距地面的高度约为多少米?(注:额头到地面的距离以身高计,sin53°≈0.8,cos53°=0.6,cot53°≈0.75, .)
(1)、求证:AC=BC.(2)、求证:DE是⊙O的切线.20. 某校为检测师生体温,在校门安装了某型号的测温门,如图为该“测温门”截面示意图.身高1.6米的小聪做了如下实验:当他在地面M处时“测温门”开始显示额头温度,此时在额头B处测得A的仰角为30°;当他在地面N处时,“测温门”停止显示额头温度,此时在额头C处测得A的仰角为53°.如果测得小聪的有效测温区间MN的长度是0.98米,求测温门顶部A处距地面的高度约为多少米?(注:额头到地面的距离以身高计,sin53°≈0.8,cos53°=0.6,cot53°≈0.75, .) 21. 如图,在 的正方形网格中,有部分网格线被擦去.点 , , 在格点(正方形网格的交点)上.
21. 如图,在 的正方形网格中,有部分网格线被擦去.点 , , 在格点(正方形网格的交点)上. (1)、请用无刻度的直尺在图1中找到三角形 的外心 ;(2)、请用无刻度的直尺在图2中找到三角形 的内心 .22. 如图, 中, 为 的内心, 为 上一点,过 两点的⊙ 交 于 点, .
(1)、请用无刻度的直尺在图1中找到三角形 的外心 ;(2)、请用无刻度的直尺在图2中找到三角形 的内心 .22. 如图, 中, 为 的内心, 为 上一点,过 两点的⊙ 交 于 点, . (1)、求线段 的长;(2)、求线段BC的长.23. 定义:我们把圆心在 的边上,与 的一边相切,且经过 的一个顶点(非切点)的圆叫做 的伴切圆.(1)、已知在 中, , , 是 的伴切圆,且点 在 上,求 的长;(2)、在平面直角坐标系中,直线 与 轴正半轴交于点 ,与 轴交于点 ,半径为3的 是 的伴切圆且圆心 在 上,直接写出所有满足条件的 的值.24. 如图, 的半径是3,点 是 上一点,弦 垂直平分线段 ,点 是 上的任意一点(不与 , 重合), 于点 ,以 为圆心, 为半径作 ,分别过 , 两点作 的切线,切点分别为 , ,两切线交于点 .
(1)、求线段 的长;(2)、求线段BC的长.23. 定义:我们把圆心在 的边上,与 的一边相切,且经过 的一个顶点(非切点)的圆叫做 的伴切圆.(1)、已知在 中, , , 是 的伴切圆,且点 在 上,求 的长;(2)、在平面直角坐标系中,直线 与 轴正半轴交于点 ,与 轴交于点 ,半径为3的 是 的伴切圆且圆心 在 上,直接写出所有满足条件的 的值.24. 如图, 的半径是3,点 是 上一点,弦 垂直平分线段 ,点 是 上的任意一点(不与 , 重合), 于点 ,以 为圆心, 为半径作 ,分别过 , 两点作 的切线,切点分别为 , ,两切线交于点 . (1)、求弦 的长;(2)、求 的大小;(3)、设 的面积为 ,若 ,求 的半径.
(1)、求弦 的长;(2)、求 的大小;(3)、设 的面积为 ,若 ,求 的半径.