新疆乌鲁木齐市两校2021年数学中考一模联考试卷

试卷更新日期：2021-05-11 类型：中考模拟

进入出卷网下载

一、单选题

1. 3的相反数是（）

A、 $\frac{1}{3}$ B、 $- \frac{1}{3}$ C、3 D、﹣3

查看试题解析
2. 下面简单几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
3. 数据85000000用科学记数法可表示为（）

A、0.85×10⁸ B、8.5×10⁶ C、8.5×10⁷ D、85×10⁶

查看试题解析
4. 下列运算正确的是（）

A、（﹣2a³）²＝4a⁶ B、a²•a³＝a⁶ C、3a+a²＝3a³ D、（a﹣b）²＝a²﹣b²

查看试题解析
5. 如图，∠BAC＝35°，∠CBD＝65°，AE∥BC，则∠CAE的度数为（）

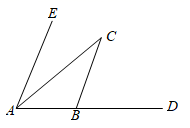A、50° B、40° C、30° D、20°

查看试题解析
6. 某班级开展“好书伴成长”读书活动，统计了1至7月份该班同学每月阅读课外书的数量，绘制了折线统计图，下列说法正确的是（）

A、每月阅读课外书本数的众数是45 B、每月阅读课外书本数的中位数是58 C、从2到6月份阅读课外书的本数逐月下降 D、从1到7月份每月阅读课外书本数的最大值比最小值多45

查看试题解析
7. 电影《我和我的祖国》一上映，第一天票房约3亿元，以后每天票房按相同的增长率增长，三天后累计票房收入达10亿元，若增长率记作x，方程可以列为（）

A、3（1+x）＝10 B、3 （1+x）²＝10 C、3+3（1+x）²＝10 D、3+3（1+x）+3（1+x）²＝10

查看试题解析
8. 如图，在Rt△ABC中，∠BAC=90°，以点A为圆心，以AB长为半径作弧交BC于点D，再分别以点B，D为圆心，以大于 $\frac{1}{2}$ BD的长为半径作弧，两弧交于点P，作射线AP交BC于点E，若AB=3，AC=4，则CD=（）

A、 $\frac{12}{5}$ B、 $\frac{9}{5}$ C、 $\frac{8}{5}$ D、 $\frac{7}{5}$

查看试题解析
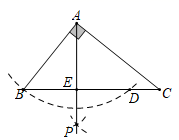9. 如图，在Rt△ABC中，∠ACB＝90°，AC＝BC＝2 $\sqrt{2}$ ，CD⊥AB于点D.点P从点A出发，沿A→D→C的路径运动，运动到点C停止，过点P作PE⊥AC于点E，作PF⊥BC于点F.设点P运动路程为x，四边形CEPF的面积为y，则能反映y与x之间函数关系图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题

10. 分解因式： $x y^{2} - 4 x =$ ．

查看试题解析
11. 一个多边形的内角和等于它的外角和的2倍，则这个多边形的边数是.

查看试题解析
12. 已知点A（1，m），B（2，n）在反比例函数 $y = - \frac{2}{x}$ 图象上，则m与n的大小关系为.

查看试题解析
13. 在一个不透明的袋子里，有2个黑球和1个白球，除了颜色外全部相同，任意摸两个球，摸到1黑1白的概率是．

查看试题解析
14. 已知每个正方形网格中正方形的边长都是1，图中的阴影部分图案是以格点为圆心，半径为1的圆弧围成的，则阴影部分的面积是.

查看试题解析
15. 如图，动点M在边长为2的正方形ABCD内，且AM⊥BM，P是CD边上的一个动点，E是AD边的中点，则线段PE+PM的最小值为.

查看试题解析

三、解答题

16. 计算：（﹣1）²⁰²⁰+|1﹣ $\sqrt{2}$ |﹣（ $\frac{1}{2}$ ）^﹣¹.

查看试题解析
17. 先化简，再求值： $\frac{a + 1}{a^{2} - 2 a + 1} \div (2 + \frac{3 - a}{a - 1})$ ，其中a=2．

查看试题解析
18. 如图，四边形ABCD是平行四边形，∠BAD的角平分线AE交CD于点F，交BC的延长线于点E.

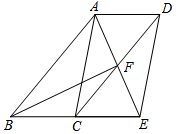(1)、求证：BE＝CD；

(2)、若BF恰好平分∠ABE，连接AC、DE，求证：四边形ACED是平行四边形.

查看试题解析
19. 在4月23日“世界读书日”来临之际，某校为了了解学生的课外阅读情况，从全校随机抽取了部分学生，调查了他们平均每周的课外阅读时间t（单位：小时）．把调查结果分为四档，A档： $t < 8$ ；B档： $8 \leq t < 9$ ；C档： $9 \leq t < 10$ ；D档： $t \geq 10$ ．根据调查情况，给出了部分数据信息：
①A档和D档的所有数据是：7，7，7.5，10，7，10，7，7.5，7，7，10.5，10.5；

②图1和图2是两幅不完整的统计图．

根据以上信息解答问题：

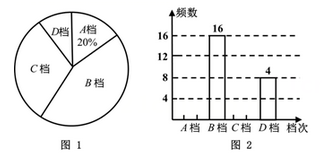(1)、求本次调查的学生人数，并将图2补充完整；

(2)、已知全校共1200名学生，请你估计全校B档的人数；

(3)、学校要从D档的4名学生中随机抽取2名作读书经验分享，已知这4名学生1名来自七年级，1名来自八年级，2名来自九年级，请用列表或画树状图的方法，求抽到的2名学生来自不同年级的概率．

查看试题解析
20. 如图，放置在水平桌面的台灯的灯臂AB长为40cm，灯罩BC长为30cm，底座厚度为2cm，灯臂与底座构成的∠A=60°，使用发现，光线最佳时灯罩BC与水平线所成的角为30°，此时灯罩顶端C到桌面的高度CE是多少？（结果精确到1cm，参考数据： $\sqrt{3}$ ≈1.73）

查看试题解析
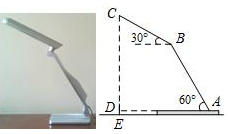21. 快车和慢车分别从A市和B市两地同时出发，匀速行驶，先相向而行，慢车到达A市后停止行驶，快车到达B市后，立即按原路原速度返回A市（调头时间忽略不计），结果与慢车同时到达A市.快、慢两车距B市的路程y₁、y₂（单位：km）与出发时间x（单位：h）之间的函数图象如图所示.

(1)、A市和B市之间的路程是km；

(2)、求a的值，并解释图中点M的横坐标、纵坐标的实际意义；

(3)、快车与慢车迎面相遇以后，再经过多长时间两车相距20km？

查看试题解析
22. 如图，以O为圆心，AB长为直径作圆，在⊙O上取一点C，延长AB至点D，连接DC，过点A作⊙O的切线交DC的延长线于点E，且∠DCB=∠DAC.

(1)、求证：CD是⊙O的切线；

(2)、若AD=6，tan∠DCB= $\frac{2}{3}$ ，求CE的长.

查看试题解析
23. 如图，已知抛物线y=﹣x²+2x+3与x轴交于A，B两点（点A在点B的左边），与y轴交于点C，连接BC．

(1)、求A，B，C三点的坐标；

(2)、若点P为线段BC上一点（不与B，C重合），PM∥y轴，且PM交抛物线于点M，交x轴于点N，当△BCM的面积最大时，求△BPN的周长；

(3)、在（2）的条件下，当△BCM的面积最大时，在抛物线的对称轴上存在一点Q，使得△CNQ为直角三角形，求点Q的坐标．

查看试题解析