四川省眉山市东坡区2021年数学中考模拟试卷
试卷更新日期:2021-05-11 类型:中考模拟
一、单选题
-
1. 2的相反数是( )A、 B、 C、2 D、-22. 2020年在疫情巨大冲击下我国能够保持就业大局稳定,城镇新增就业1186万人.现将数据1186万用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 下列几何体是由4个相同的小正方体搭成的,其中,主视图、左视图、俯视图都相同的是( )A、
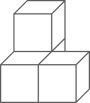 B、
B、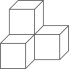 C、
C、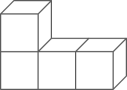 D、
D、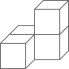 5. 某数学兴趣小组为了解我市气温变化情况,记录了今年3月份连续6天的最低气温(单位:℃):13,7,10,8,10,12.关于这组数据,下列结论不正确的是( )A、平均数是10 B、众数是10 C、中位数是10 D、方差是46. 一副三角板如图摆放,且 ,则 的度数为( )
5. 某数学兴趣小组为了解我市气温变化情况,记录了今年3月份连续6天的最低气温(单位:℃):13,7,10,8,10,12.关于这组数据,下列结论不正确的是( )A、平均数是10 B、众数是10 C、中位数是10 D、方差是46. 一副三角板如图摆放,且 ,则 的度数为( )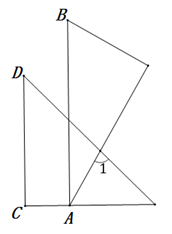 A、 B、 C、 D、7. 已知 ,则代数式 的值是( )A、-30 B、20 C、-10 D、08. 如图,在 中, 、 为边 的三等分点, ,点 为 与 的交点.若 ,则 为( )
A、 B、 C、 D、7. 已知 ,则代数式 的值是( )A、-30 B、20 C、-10 D、08. 如图,在 中, 、 为边 的三等分点, ,点 为 与 的交点.若 ,则 为( )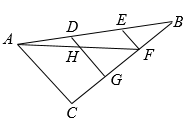 A、1 B、2 C、 D、39. 如图,点 、 、 是 上的三个点, , ,则 的度数为( )
A、1 B、2 C、 D、39. 如图,点 、 、 是 上的三个点, , ,则 的度数为( )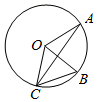 A、 B、 C、 D、10. 若关于 的不等式组 的解集是 ,则 的取值范围是( )A、 B、 C、 D、11. 已知m、n、4分别是等腰三角形(非等边三角形)三边的长,且m、n是关于x的一元二次方程 ﹣6x+k+2=0的两个根,则k的值等于( )A、7 B、7或6 C、6或﹣7 D、612. 如图,在 中, , , 于点D , 于点E , .连接DE , 将 沿直线AE翻折至 所在的平面内,得 ,连接DF . 过点D作 交BE于点G . 则四边形DFEG的周长为( )
A、 B、 C、 D、10. 若关于 的不等式组 的解集是 ,则 的取值范围是( )A、 B、 C、 D、11. 已知m、n、4分别是等腰三角形(非等边三角形)三边的长,且m、n是关于x的一元二次方程 ﹣6x+k+2=0的两个根,则k的值等于( )A、7 B、7或6 C、6或﹣7 D、612. 如图,在 中, , , 于点D , 于点E , .连接DE , 将 沿直线AE翻折至 所在的平面内,得 ,连接DF . 过点D作 交BE于点G . 则四边形DFEG的周长为( )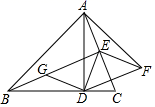 A、8 B、 C、 D、
A、8 B、 C、 D、二、填空题
-
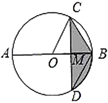
13. 分解因式: =.14. 不透明袋子中装有7个球,其中有2个红球、5个黑球,这些球除颜色外无其他差别从袋子中随机取出1个球,则它是红球的概率是.15. 将抛物线 向右平移个单位长度后经过点 .16. 若 , 是方程 的两个实数根,则代数式 的值等于.17. 如图, 是 的直径,弦 ,垂足为点 ,连接 、 .如果 ,图中阴影部分的面积是 ,则 的长为.
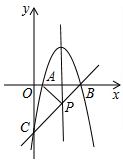
 18. 如图,平面直角坐标系中, 为原点,点 、 分别在 轴、 轴的正半轴上, 的两条外角平分线交于点 ,且点 在反比例函数 的图象上. 、 的延长线分别交 轴、 轴于点 、 ,连结 ,则 的面积是.
18. 如图,平面直角坐标系中, 为原点,点 、 分别在 轴、 轴的正半轴上, 的两条外角平分线交于点 ,且点 在反比例函数 的图象上. 、 的延长线分别交 轴、 轴于点 、 ,连结 ,则 的面积是.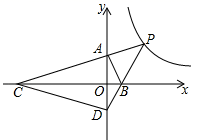
三、解答题
-
19. 计算:20. 先化简,再求值: ,其中 .21. 如图,一次函数 的图象与反比例函数 ( 为常数且 )的图象相交于 ,B两点.
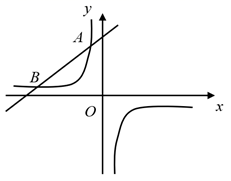 (1)、求反比例函数的表达式;(2)、将一次函数 的图象沿 轴向下平移 个单位 ,使平移后的图象与反比例函数 的图象有且只有一个交点,求b的值.22. 防疫期间,全市所有学校都严格落实测体温进校园的防控要求.某校开设了A、B、C三个测温通道,某天早晨,该校小明和小丽两位同学将随机通过测温通道进入校园.(1)、小明从A测温通道通过的概率是;(2)、利用画树状图或列表的方法,求小明和小丽从同一个测温通道通过的概率.23. 超速行驶是一种十分危险的违法驾驶行为,在一条笔直的高速公路MN上,小型车限速为每小时120千米,设置在公路旁的超速监测点C,现测得一辆小型车在监测点C的南偏西30°方向的A处,7秒后,测得其在监测点C的南偏东45°方向的B处,已知BC=200米,B在A的北偏东75°方向,请问:这辆车超速了吗?通过计算说明理由.(参考数据: ≈1.41, ≈1.73)
(1)、求反比例函数的表达式;(2)、将一次函数 的图象沿 轴向下平移 个单位 ,使平移后的图象与反比例函数 的图象有且只有一个交点,求b的值.22. 防疫期间,全市所有学校都严格落实测体温进校园的防控要求.某校开设了A、B、C三个测温通道,某天早晨,该校小明和小丽两位同学将随机通过测温通道进入校园.(1)、小明从A测温通道通过的概率是;(2)、利用画树状图或列表的方法,求小明和小丽从同一个测温通道通过的概率.23. 超速行驶是一种十分危险的违法驾驶行为,在一条笔直的高速公路MN上,小型车限速为每小时120千米,设置在公路旁的超速监测点C,现测得一辆小型车在监测点C的南偏西30°方向的A处,7秒后,测得其在监测点C的南偏东45°方向的B处,已知BC=200米,B在A的北偏东75°方向,请问:这辆车超速了吗?通过计算说明理由.(参考数据: ≈1.41, ≈1.73)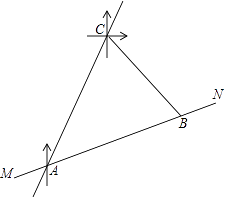 24. 超市销售某品牌洗手液,进价为每瓶10元.在销售过程中发现,每天销售量y(瓶)与每瓶售价x(元)之间满足一次函数关系(其中 ,且 为整数),当每瓶洗手液的售价是12元时,每天销售量为90瓶;当每瓶洗手液的售价是14元时,每天销售量为80瓶.(1)、求y与x之间的函数关系式;(2)、设超市销售该品牌洗手液每天销售利润为w元,当每瓶洗手液的售价定为多少元时,超市销售该品牌洗手液每天销售利润最大,最大利润是多少元?
24. 超市销售某品牌洗手液,进价为每瓶10元.在销售过程中发现,每天销售量y(瓶)与每瓶售价x(元)之间满足一次函数关系(其中 ,且 为整数),当每瓶洗手液的售价是12元时,每天销售量为90瓶;当每瓶洗手液的售价是14元时,每天销售量为80瓶.(1)、求y与x之间的函数关系式;(2)、设超市销售该品牌洗手液每天销售利润为w元,当每瓶洗手液的售价定为多少元时,超市销售该品牌洗手液每天销售利润最大,最大利润是多少元?