江苏省南通市2021年数学中考模拟试卷
试卷更新日期:2021-05-11 类型:中考模拟
一、单选题
-
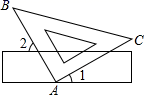
1. 计算|﹣1|﹣3,结果正确的是( )A、﹣4 B、﹣3 C、﹣2 D、﹣12. 345万这个数用科学记数法表示为( )A、 0.345×107 B、3.45×106 C、34.5×105 D、345×1043. 如图,把三角尺的直角顶点放在直尺的一边上,若∠1=32°,则∠2的度数为( )
 A、68° B、58° C、48° D、32°4. 计算 的结果是( )A、 B、 C、 D、5. 在平面直角坐标系中,点G的坐标是 ,连接 ,将线段 绕原点O旋转 ,得到对应线段 ,则点 的坐标为( )A、 B、 C、 D、6. 在一次献爱心的捐款活动中,八(2)班50名同学捐款金额如图所示,则在这次捐款活动中,该班同学捐款金额的众数和中位数分别是( )
A、68° B、58° C、48° D、32°4. 计算 的结果是( )A、 B、 C、 D、5. 在平面直角坐标系中,点G的坐标是 ,连接 ,将线段 绕原点O旋转 ,得到对应线段 ,则点 的坐标为( )A、 B、 C、 D、6. 在一次献爱心的捐款活动中,八(2)班50名同学捐款金额如图所示,则在这次捐款活动中,该班同学捐款金额的众数和中位数分别是( )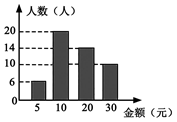 A、20,10 B、10,20 C、10,10 D、10,157. 下列条件中,能判断四边形是菱形的是( )A、对角线互相垂直且相等的四边形 B、对角线互相垂直的四边形 C、对角线相等的平行四边形 D、对角线互相平分且垂直的四边形8. 如图是一个几体何的三视图(图中尺寸单位:cm),则这个几何体的侧面积为( )
A、20,10 B、10,20 C、10,10 D、10,157. 下列条件中,能判断四边形是菱形的是( )A、对角线互相垂直且相等的四边形 B、对角线互相垂直的四边形 C、对角线相等的平行四边形 D、对角线互相平分且垂直的四边形8. 如图是一个几体何的三视图(图中尺寸单位:cm),则这个几何体的侧面积为( )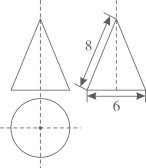 A、48πcm2 B、24πcm2 C、12πcm2 D、9πcm29. 如图,点P是边长为2cm的正方形ABCD的边上一动点,O是对角线的交点,当点P由A→D→C运动时,设P点运动的路程为xcm,则 POD的面积y(cm2)随x(cm)变化的关系图象为( )
A、48πcm2 B、24πcm2 C、12πcm2 D、9πcm29. 如图,点P是边长为2cm的正方形ABCD的边上一动点,O是对角线的交点,当点P由A→D→C运动时,设P点运动的路程为xcm,则 POD的面积y(cm2)随x(cm)变化的关系图象为( )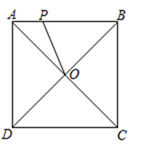 A、
A、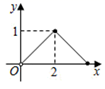 B、
B、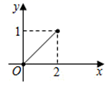 C、
C、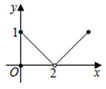 D、
D、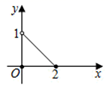 10. 在抛物线y=a(x﹣m﹣1)2+c(a≠0)和直线y=﹣ x的图象上有三点(x1 , m)、(x2 , m)、(x3 , m),则x1+x2+x3的结果是( )A、 B、0 C、1 D、2
10. 在抛物线y=a(x﹣m﹣1)2+c(a≠0)和直线y=﹣ x的图象上有三点(x1 , m)、(x2 , m)、(x3 , m),则x1+x2+x3的结果是( )A、 B、0 C、1 D、2二、填空题
-
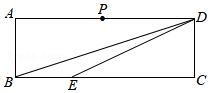
11. 分解因式:xy﹣2y2=.12. 已知⊙O的半径为13cm,弦AB的长为10cm,则圆心O到AB的距离为cm.13. 若一次函数y=(1-m)x+2,函数值y随x的增大而减小,则m的取值范围是 .14. 如图,在矩形ABCD中,BC=3CD= ,点P是AD的中点,点E在BC上,CE=2BE,点M、N在线段BD上.若 PMN是等腰三角形且底角与∠DEC相等,则PN=.
 15. 中国古代数学家杨辉的《田亩比数乘除减法》中记载:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步?翻译成数学问题是:一块矩形田地的面积为864平方步,它的宽比长少12步,问它的长与宽各多少步?利用方程思想,设宽为x步,则依题意列方程为 .16. 如图,利用标杆 测量楼房 的高度,如果标杆 长为3. 6米,若 , 米,则楼高是米.
15. 中国古代数学家杨辉的《田亩比数乘除减法》中记载:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步?翻译成数学问题是:一块矩形田地的面积为864平方步,它的宽比长少12步,问它的长与宽各多少步?利用方程思想,设宽为x步,则依题意列方程为 .16. 如图,利用标杆 测量楼房 的高度,如果标杆 长为3. 6米,若 , 米,则楼高是米.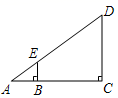 17. 若x1和x2为一元二次方程x2+2x﹣1=0的两个根.则x12x2+x1x22值为.18. 如图,在平面直角坐标系中,菱形 的顶点 在坐标原点,边 在 轴的负半轴上, ,顶点 的坐标为 ,反比例函数 的图象与菱形对角线 交于 点,连接 ,当 轴时, 的值是.
17. 若x1和x2为一元二次方程x2+2x﹣1=0的两个根.则x12x2+x1x22值为.18. 如图,在平面直角坐标系中,菱形 的顶点 在坐标原点,边 在 轴的负半轴上, ,顶点 的坐标为 ,反比例函数 的图象与菱形对角线 交于 点,连接 ,当 轴时, 的值是.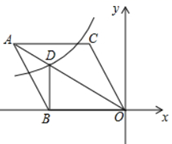
三、解答题
-
19. 计算:(1)、 ;(2)、 .20. 如图,已知直线l1经过点A(5,0),B(1,4),与直线l2:y=2x﹣4交于点C,且直线l2交x轴于点D.
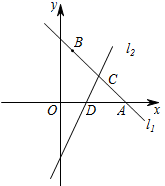 (1)、求直线l1的函数表达式;(2)、求 ADC的面积.21. 如图,AB是⊙O的直径,C 是⊙O上一点,过点C 作⊙O的切线,交BA的延长线交于点D,过点B 作BE⊥BA,交DC延长线于点E,连接OE,交⊙O于点F,交BC于点H,连接AC.
(1)、求直线l1的函数表达式;(2)、求 ADC的面积.21. 如图,AB是⊙O的直径,C 是⊙O上一点,过点C 作⊙O的切线,交BA的延长线交于点D,过点B 作BE⊥BA,交DC延长线于点E,连接OE,交⊙O于点F,交BC于点H,连接AC.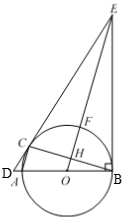 (1)、求证:∠ECB=∠EBC;(2)、连接BF,CF,若BF=5,sin∠FBC= ,求AC的长.22. 某工厂甲、乙两个部门各有员工400人,为了了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
(1)、求证:∠ECB=∠EBC;(2)、连接BF,CF,若BF=5,sin∠FBC= ,求AC的长.22. 某工厂甲、乙两个部门各有员工400人,为了了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.收集数据从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如表:
甲
78
86
74
81
75
76
87
70
75
90
75
79
81
70
74
80
86
69
83
77
乙
93
73
88
81
72
81
94
83
77
83
80
81
70
81
73
78
82
80
70
40
整理、描述数据按如下分数段整理、描述这两组样本数据:
成绩x人数
部门
40≤x≤49
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
甲
0
0
1
11
7
1
乙
1
0
0
7
10
2
(说明:成绩80分及以上为生产技能优秀,70~79分为生产技能良好,60~69分为生产技能合格,60分以下为生产技能不合格)
分析数据两组样本数据的平均数、中位数、众数如表所示:
部门
平均数
中位数
众数
方差
甲
78.3
77.5
m
33.61
乙
78
n
81
117.5
得出结论
(1)、上表中m= , n=;(2)、甲、乙两个部门员工的生产技能水平比较均衡的是部门,估计乙部门生产技能优秀的员工人数为;(3)、可以推断出部门员工的生产技能水平较高,理由为.(至少从两个不同的角度说明推断的合理性)23. 某商场举办抽奖活动,规则如下:在不透明的袋子中有2个黑球和2个红球,这些球除颜色外都相同.顾客每次摸出一个球,若摸到黑球,则获得1份奖品;若摸到红球,则没有奖品.(1)、如果小芳只有一次摸球机会,那么小芳获得奖品的概率为;(2)、如果小芳有两次摸球机会(摸出后不放回),求小芳获得2份奖品的概率.24. 如图,点 分别在矩形 的边 上,连接 ,将 沿直线 翻折得到 ,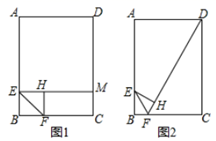 (1)、如图1,当 时, 的延长线交 于点 ,求 的长(2)、如图2当 的延长线经过点 时,求 的值;25. 在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m﹣4与x轴交于点A,B(点A在点B的左侧),与y轴交于点C(0,﹣3).
(1)、如图1,当 时, 的延长线交 于点 ,求 的长(2)、如图2当 的延长线经过点 时,求 的值;25. 在平面直角坐标系xOy中,抛物线y=x2﹣2mx+m﹣4与x轴交于点A,B(点A在点B的左侧),与y轴交于点C(0,﹣3).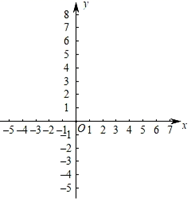 (1)、求m的值;(2)、若一次函数y=kx+5(k≠0)的图象经过点A,求k的值;(3)、将二次函数的图象在点B,C间的部分(含点B和点C)向左平移n(n>0)个单位后得到的图象记为G,同时将(2)中得到的直线y=kx+5(k≠0)向上平移n个单位,当平移后的直线与图象G有公共点时,请结合图象直接写出n的取值范围.26. 定义:有一个内角为90°,且对角线相等的四边形称为准矩形.(1)、如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=4,则BD=;
(1)、求m的值;(2)、若一次函数y=kx+5(k≠0)的图象经过点A,求k的值;(3)、将二次函数的图象在点B,C间的部分(含点B和点C)向左平移n(n>0)个单位后得到的图象记为G,同时将(2)中得到的直线y=kx+5(k≠0)向上平移n个单位,当平移后的直线与图象G有公共点时,请结合图象直接写出n的取值范围.26. 定义:有一个内角为90°,且对角线相等的四边形称为准矩形.(1)、如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=4,则BD=;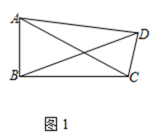 (2)、如图2,正方形ABCD中,点E,F分别是边AD,AB上的点,且CF⊥BE,求证:四边形BCEF是准矩形;
(2)、如图2,正方形ABCD中,点E,F分别是边AD,AB上的点,且CF⊥BE,求证:四边形BCEF是准矩形;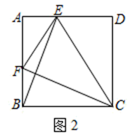 (3)、如图3,准矩形ABCD中,∠ABC=90°,∠BAC=60°,AB=2,AC=DC,求这个准矩形的面积.
(3)、如图3,准矩形ABCD中,∠ABC=90°,∠BAC=60°,AB=2,AC=DC,求这个准矩形的面积.