浙江省绍兴市2020-2021学年八年级下学期数学期中考试试卷

试卷更新日期：2021-05-11 类型：期中考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列图形既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 用配方法解方程x²﹣4x＝1时，原方程应变形为（）

A、（x﹣2）²＝1 B、（x+2）²＝5 C、（x+2）²＝1 D、（x﹣2）²＝5

查看试题解析
3. 小明的作业上有如下的题目，计算错误的是（）

A、 $\sqrt{16 a^{4}}$ ＝4a² B、 $\sqrt{5 a} \cdot \sqrt{10 a}$ ＝5 $\sqrt{2}$ a C、 $\sqrt{3} a - \sqrt{2} a$ ＝ $\sqrt{a}$ D、3 $\sqrt{2}$ +2 $\sqrt{2}$ ＝5 $\sqrt{2}$

查看试题解析
4. 学习组织“超强大脑”答题赛，参赛的12名选手得分情况如表所示，那么这12名选手得分的中位数和众数分别是（）

分数（分）

60

80

90

95

人数（人）

3

2

3

4

A、80和90 B、90和95 C、86.5和90 D、90和90

查看试题解析
5. 关于x的方程x²+4x+a＝0有两个不相等的实数根，则a的值可能为（）

A、3 B、4 C、5 D、6

查看试题解析
6. 有理数a和b在数轴上的位置如图所示，则 $\sqrt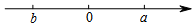{b^{2}}$ ﹣|a﹣b|等于（）

A、a B、﹣a C、2b+a D、2b﹣a

查看试题解析
7. 给出以下方程的解题过程，其中正确的有（）
①解方程 $\frac{1}{2}$ （x﹣2）²＝16，两边同时开方得x﹣2＝±4，移项得x₁＝6，x₂＝﹣2；②解方程x（x﹣ $\frac{1}{2}$ ）＝（x﹣ $\frac{1}{2}$ ），两边同时除以（x﹣ $\frac{1}{2}$ ）得x＝1，所以原方程的根为x₁＝x₂＝1；③解方程（x﹣2）（x﹣1）＝5，由题得x﹣2＝1，x﹣1＝5，解得x₁＝3，x₂＝6；④方程（x﹣m）²＝n的解是x₁＝m+ $\sqrt{n}$ ，x₂＝m﹣ $\sqrt{n}$ ．

A、0个 B、2个 C、3个 D、4个

查看试题解析
8. 若方程x²﹣8x+m＝0可通过配方写成（x﹣n）²＝6的形式，则x²+8x+m＝5可配方成（）

A、（x﹣n+5）²＝1 B、（x+n）²＝1 C、（x﹣n+5）²＝11 D、（x+n）²＝11

查看试题解析
9. 如图，点A是直线l外一点，在l上取两点B ， C ，分别以A ， C为圆心，BC ， AB长为半径画弧，两弧相交于点D ，分别连接AB ， AD ， CD ，则四边形ABCD的（）

A、四条边相等 B、四个角相等 C、对角线互相垂直 D、对角线互相平分

查看试题解析
10. 现有12块完全相同的巧克力，每块至多被分为两小块，如果这12块巧克力可以平均分给n名同学，则n不可以为（）

A、20 B、18 C、15 D、14

查看试题解析

二、填空题（每题3分，共24分）

11. 若二次根式 $\sqrt{x - 2}$ 有意义，则x的取值范围是．

查看试题解析
12. 计算 $\sqrt{2 a}$ × $\sqrt{8 a}$ （a≥0）的结果是．

查看试题解析
13. 若一组数据1，3，a ， 2，5的平均数是3，则a＝。

查看试题解析
14. 我们知道若关于x的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 有一根是1，则a+b+c=0，那么如果 $9 a + c = 3 b$ ，则方程 $a x^{2} + b x + c = 0$ 有一根为

查看试题解析
15. 如图，平行四边形ABCD中，点O是对角线AC的中点，点E在边AB上，连接DE ，取DE的中点F ，连接EO并延长交CD于点G ．若BE＝3CG ， OF＝2，则线段AE的长是．

查看试题解析
16. 如图：在六边形ABCDEF中，AB‖DE，BC‖EF，CD‖AF，∠A=150°，则∠C+∠E=.

查看试题解析
17. 如图，在▱ABCD中，P是对角线BD上的一点，过点P作EF∥AB，与AD和BC分别交于点E和点F ，连接AP ， CP ．已知AE＝4，EP＝2，∠ABC＝60°，则阴影部分的面积是

查看试题解析
18. 在平面直角坐标系中，A（﹣1，1），B（2，3），C（3m ， 4m+1），D在x轴上，若以A ， B ， C ， D四点为顶点的四边形是平行四边形，求点D的坐标.

查看试题解析

三、解答题：（共6小题，其中第19.21.22.23每题6分，第20题12分,第24题10分，共46分）

19. 计算：

(1)、 $\sqrt{12} - | 1 - 2 \sqrt{3} | + （ \frac{1}{3} ）^{- 2} + （ π + \sqrt{2} ）^{0}$ ；

(2)、 $\sqrt{18} - \sqrt{8} + （ \sqrt{3} + 1 ）（ \sqrt{3} - 1 ）$

查看试题解析
20. 解下列一元二次方程:

(1)、 $3 （ 2 x - 1 ）^{2} - 12 = 0$

(2)、 $2 x^{2} - 4 x - 7 = 0$

(3)、 $x^{2} + x - 1 = 0$

(4)、 $（ 2 x - 1 ）^{2} - x^{2} = 0$

查看试题解析
21. 如图，在△ABC中，AB＝13，AC＝23，点D在AC上，若BD＝CD＝10，AE平分∠BAC ．

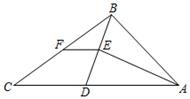(1)、求AE的长；

(2)、若F是BC中点，求线段EF的长．

查看试题解析
22. 某商贸公司10名销售员3月份完成的销售额情况如下表:

销售额(万元)

3

4

5

6

7

8

16

销售员人数

1

1

3

2

1

1

1

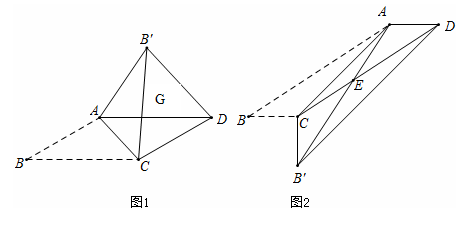
(1)、销售额的中位数是万元,众数万元,平均每人完成的销售额万元,

(2)、其中有位销售员甲3月份的销售额是8万元，计划到5月份增长到12.5万元,求每月的平均增长率.

查看试题解析
23. 宾馆有50间房供游客居住，原定价每间房每天190元．当每间房每天定价为180元时，宾馆会住满；当每间房每天的定价每增加10元时，就会空闲一间房（物价部门规定，此类宾馆的入住费用不得超过原定价的1.5倍）．如果有游客居住，宾馆需对居住的每间房每天支出20元的费用．

(1)、如果每间房当天的定价比房间住满时的房价增加x元时，宾馆间房有游客居住（用含x的代数式表示）；

(2)、当房价定为多少元时，宾馆当天的利润为9450元？

查看试题解析
24. 我们知道平行四边形有很多性质．现在如果我们把平行四边形沿着它的一条对角线翻折．会发现这其中还有更多的结论，如图，已知平行四边形ABCD中，AB=2 $\sqrt{3}$ ， ∠30°，AB≠BC，将△ABC沿AC翻折至△AB′C，连接B′D．

(1)、【发现与证明】
如图1：结论①△AGC是等腰三角形；结论②B′D∥AC。请证明结论①或结论②（只需证明一个结论）。

(2)、【应用与解答】
如图2：如果BC=1，AB′与CD相交于点E，求△AEC的面积。

(3)、【拓展与探索】
直接写出结论，当BC的长为多少时，△AB′D是直角三角形？

查看试题解析

分数（分）	60	80	90	95
人数（人）	3	2	3	4

销售额(万元)	3	4	5	6	7	8	16
销售员人数	1	1	3	2	1	1	1