浙江省宁波市北仑区2020-2021学年八年级下学期数学期中考试试卷
试卷更新日期:2021-05-11 类型:期中考试
一、选择题(每小题3分,共36分)
-
1. 二次根式 中字母a的取值范围是( )A、a<1 B、a>1 C、a≤1 D、a≥12. 下列图形中,既是轴对称图形又是中心对称图形的有( )
 A、4个 B、3个 C、2个 D、1个3. 已知 ABCD中,∠A+∠C=200°,则∠B的度数是( )A、100° B、160° C、80° D、60°4. 下列方程是一元二次方程的是( )A、﹣6x+2=0 B、2x2﹣y+1=0 C、x2+2x=0 D、 +x=25. 下列计算正确的是( )A、 ﹣ = B、 + = C、 = × D、 ÷ =46. 一元二次方程x2﹣2x﹣1=0的根的情况为( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根7. 甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数都约为8.8环,方差分别为S = 0.63环2 , S = 0.51环2 , S = 0.48环2 , S = 0.42环2 , 则四人中成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁8. 将方程x2﹣6x+1=0配方后,原方程变形为( )A、(x﹣3)2=8 B、(x﹣3)2=﹣8 C、(x﹣3)2=9 D、(x﹣3)2=﹣99. 用反证法证明“在直角三角形中,至少有一个锐角不大于45º”,应先假设这个直角三角形中( )A、有一个锐角小于45º B、每一个锐角都小于45º C、有一个锐角大于45º D、每一个锐角都大于45º10. 如图,在一个长方形舞台ABCD中铺上一块正方形的地毯,供演出用。已知长方形舞台的面积为30 m2 , 若正方形的边长为x m,则下列关于x方程正确的是 ( )
A、4个 B、3个 C、2个 D、1个3. 已知 ABCD中,∠A+∠C=200°,则∠B的度数是( )A、100° B、160° C、80° D、60°4. 下列方程是一元二次方程的是( )A、﹣6x+2=0 B、2x2﹣y+1=0 C、x2+2x=0 D、 +x=25. 下列计算正确的是( )A、 ﹣ = B、 + = C、 = × D、 ÷ =46. 一元二次方程x2﹣2x﹣1=0的根的情况为( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根7. 甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数都约为8.8环,方差分别为S = 0.63环2 , S = 0.51环2 , S = 0.48环2 , S = 0.42环2 , 则四人中成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁8. 将方程x2﹣6x+1=0配方后,原方程变形为( )A、(x﹣3)2=8 B、(x﹣3)2=﹣8 C、(x﹣3)2=9 D、(x﹣3)2=﹣99. 用反证法证明“在直角三角形中,至少有一个锐角不大于45º”,应先假设这个直角三角形中( )A、有一个锐角小于45º B、每一个锐角都小于45º C、有一个锐角大于45º D、每一个锐角都大于45º10. 如图,在一个长方形舞台ABCD中铺上一块正方形的地毯,供演出用。已知长方形舞台的面积为30 m2 , 若正方形的边长为x m,则下列关于x方程正确的是 ( ) A、(1.5+x)(1+x)=30 B、(1.5-x)(1-x)=30 C、(3+x)(2+x)=30 D、x2+2×3=3011. 如果1≤a≤ , 则 的值是( )A、6+a B、-6-a C、-a D、112. 如图,在平行四边形 中,点A1 , A2 , A3 , A4和C1 , C2 , C3 , C4分别是AB和CD的五等分点,点B1 , B2和D1 , D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为2,则平行四边形ABCD的面积为( )
A、(1.5+x)(1+x)=30 B、(1.5-x)(1-x)=30 C、(3+x)(2+x)=30 D、x2+2×3=3011. 如果1≤a≤ , 则 的值是( )A、6+a B、-6-a C、-a D、112. 如图,在平行四边形 中,点A1 , A2 , A3 , A4和C1 , C2 , C3 , C4分别是AB和CD的五等分点,点B1 , B2和D1 , D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为2,则平行四边形ABCD的面积为( )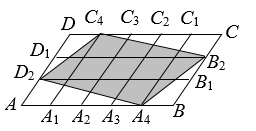 A、4 B、 C、 D、30
A、4 B、 C、 D、30二、填空题(每小题3分,共18分)
-
13. 当 =-1时,二次根式 的值是 .14. 已知一个多边形的每个外角都是30°,则这个多边形为边形15. 在平面直角坐标系中,若点P(x-2,x)关于原点的对称点在第四象限,则x的取值范围是 .16. 公园新增设了一台滑梯,该滑梯高度AC=1米,滑梯AB的坡比是1:3,则该滑梯AB的长是米.
 17. 如图,△ABC中,AB=4,AC=3,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为
17. 如图,△ABC中,AB=4,AC=3,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为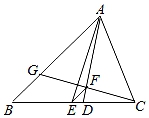 18. 对于实数a,b,定义运算“*”,a*b= 例如4*2.因为4>2,所以4*2=42﹣4×2=8,若x1、x2是一元二次方程x2﹣9x+20=0的两个根,则x1*x2= .
18. 对于实数a,b,定义运算“*”,a*b= 例如4*2.因为4>2,所以4*2=42﹣4×2=8,若x1、x2是一元二次方程x2﹣9x+20=0的两个根,则x1*x2= .三、解答题(第19题6分,第20题6分,第21、22、23、24题每题8分,第25题10分,第26题12分,共66分)
-
19. 计算(1)、(2)、20. 解方程(1)、(2)、21. 在我市开展的“好书伴我成长”读书活动中,某中学为了解八年级300名学生读书情况,随机调查了八年级50名学生读书的册数,统计数据如下表所示:
册数
0
1
2
3
4
人数
3
13
16
17
1
(1)、求这50个样本数据的平均数、众数和中位数:(2)、根据样本数据,估计该校八年级300名学生在本次活动中读书多于2册的人数.22. 图(a)、图(b)是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.请在图(a)、图(b)中,分别画出符合要求的图形,所画图形各顶点必须与方格纸中的小正方形顶点重合.具体要求如下: (1)、画一个面积为10的等腰直角三角形(2)、画一个面积为12的平行四边形23. 已知关于x的一元二次方程(a﹣3)x2﹣4x+3=0(1)、若方程的一个根为x=﹣1,求a的值;(2)、若方程有实数根,求满足条件的正整数a的值;(3)、请为a选取一个合适的整数,使方程有两个整数根,并求这两个根.24. 如图,等边△ABC的边长是2,D,E分别为AB,AC的中点,延长BC至点F,使CF= BC,连结CD和EF.
(1)、画一个面积为10的等腰直角三角形(2)、画一个面积为12的平行四边形23. 已知关于x的一元二次方程(a﹣3)x2﹣4x+3=0(1)、若方程的一个根为x=﹣1,求a的值;(2)、若方程有实数根,求满足条件的正整数a的值;(3)、请为a选取一个合适的整数,使方程有两个整数根,并求这两个根.24. 如图,等边△ABC的边长是2,D,E分别为AB,AC的中点,延长BC至点F,使CF= BC,连结CD和EF. (1)、求证:四边形CDEF是平行四边形;(2)、求四边形BDEF的周长.25. 百货商店销售某种冰箱,每台进价2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;每台售价每降低10元时,平均每天能多售出1台.(销售利润=销售价-进价)(1)、如果设每台冰箱降价x元,那么每台冰箱的销售利润为元,平均每天可销售冰箱台;(用含x的代数式表示)(2)、商店想要使这种冰箱的销售利润平均每天达到5600元,且尽可能地清空冰箱库存,每台冰箱的定价应为多少元?26. 如图,四边形ABCD中, AD∥BC,AD=15, BC=25,AB=DC=10,动点P从点D出发,以每秒1个单位长的速度沿线段DA的方向向点A运动,动点Q从点C出发,以每秒2个单位长的速度沿射线CB的方向运动,点P、Q分别从点D、C同时出发,当点P运动到点A时,点Q随之停止运动.设运动的时间为t(秒)。
(1)、求证:四边形CDEF是平行四边形;(2)、求四边形BDEF的周长.25. 百货商店销售某种冰箱,每台进价2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;每台售价每降低10元时,平均每天能多售出1台.(销售利润=销售价-进价)(1)、如果设每台冰箱降价x元,那么每台冰箱的销售利润为元,平均每天可销售冰箱台;(用含x的代数式表示)(2)、商店想要使这种冰箱的销售利润平均每天达到5600元,且尽可能地清空冰箱库存,每台冰箱的定价应为多少元?26. 如图,四边形ABCD中, AD∥BC,AD=15, BC=25,AB=DC=10,动点P从点D出发,以每秒1个单位长的速度沿线段DA的方向向点A运动,动点Q从点C出发,以每秒2个单位长的速度沿射线CB的方向运动,点P、Q分别从点D、C同时出发,当点P运动到点A时,点Q随之停止运动.设运动的时间为t(秒)。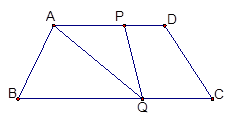 (1)、当t=2时,求△APQ的面积;(2)、若四边形ABQP为平行四边形,求运动时间t;(3)、当t为何值时,以A,P,Q三点为顶点的三角形是等腰三角形?
(1)、当t=2时,求△APQ的面积;(2)、若四边形ABQP为平行四边形,求运动时间t;(3)、当t为何值时,以A,P,Q三点为顶点的三角形是等腰三角形?