浙江省宁波市慈溪市2020-2021学年八年级下学期数学期中考试试卷

试卷更新日期：2021-05-11 类型：期中考试

进入出卷网下载

一、选择题（共10小题，满分30分，每小题3分）

1. 下列方程是一元二次方程的是（）

A、 $(x - 7) x = x^{2}$ B、 $\frac{360 °}{7}$ C、 $2 x + \frac{1}{x} + 1 = 0$ D、 $x^{2} = 1$

查看试题解析
2. 要使式子 $\frac{\sqrt{a + 2}}{a}$ 有意义， $a$ 的取值范围是（）

A、 $a \neq 0$ B、 $a > - 2$ C、 $a > - 2$ 或 $a \neq 0$ D、 $a \geq - 2$ 且 $a \neq 0$

查看试题解析
3. 一元二次方程 $4 x^{2} - 2 x + \frac{1}{4} = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断

查看试题解析
4. 华联超市4月份的营业额为220万元，5月份营业额为242万元，如果保持同样的增长率，6月份应完成营业额（）万元．

A、264 B、266.2 C、272.4 D、286

查看试题解析
5. 用配方法解一元二次方程 $x^{2} - 4 x - 1 = 0$ ，配方得到的方程是（）

A、 ${(x - 2)}^{2} = 1$ B、 ${(x - 2)}^{2} = 4$ C、 ${(x - 2)}^{2} = 5$ D、 ${(x - 2)}^{2} = 3$

查看试题解析
6. 某校规定学生的学期数学成绩满分为100分，其中研究性学习成绩占40%，期末卷面成绩占60%，小明的两项成绩（百分制）依次是80分，90分，则小明这学期的数学成绩是（）

A、80分 B、82分 C、84分 D、86分

查看试题解析
7. 下列说法：①伸缩门的制作运用了四边形的不稳定性；②夹在两条平行线间的垂线段相等；③成中心对称的两个图形不一定是全等形；④一组对角相等的四边形是平行四边形；⑤用反证法证明“四边形中至少有一个角是钝角或直角”时，必先假设“四边形中至多有一个角是钝角或直角”，其中正确的是（）

A、①② B、③④ C、①②④ D、①②⑤

查看试题解析
8. 如图，平行四边形ABCD的对角线AC与BD相交于点O ， AE⊥BC ，垂足为E ， $A B = \sqrt{3}$ ，AC＝2，BD＝4，则AE的长为（）

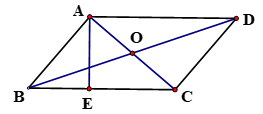A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{3}{2}$ C、 $\frac{\sqrt{21}}{7}$ D、 $\frac{2 \sqrt{21}}{7}$

查看试题解析
9. 我们知道方程 $x^{2} + 2 x - 3 = 0$ 的解是 $x_{1} = 1$ ， $x_{2} = - 3$ ，现给出另一个方程 ${(x + 3)}^{2} + 2 (x + 3) - 3 = 0$ ，它的解是（）

A、 $x_{1} = 2$ ， $x_{2} = - 6$ B、 $x_{1} = 1$ ， $x_{2} = - 3$ C、 $x_{1} = - 1$ ， $x_{2} = 3$ D、 $x_{1} = - 2$ ， $x_{2} = - 6$

查看试题解析
10. 如图，已知▱OABC的顶点A，C分别在直线 $x = 1$ 和 $x = 4$ 上，O是坐标原点，则对角线OB长的最小值为（）

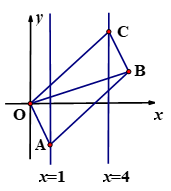A、3 B、4 C、5 D、6

查看试题解析

二、填空题（共6小题，满分24分，每小题4分）

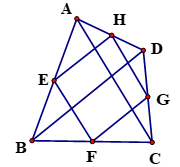
11. 一个多边形的内角和比四边形外角和的4倍多180°，这个多边形的边数是

查看试题解析
12. 平行四边形的周长为24cm ，相邻两边长的比为3︰1，那么这个平行四边形较短的边长为cm ．

查看试题解析
13. 已知 $(x^{2} + y^{2}) (x^{2} + y^{2} - 1) = 12$ ，则 $x^{2} + y^{2}$ 的值是

查看试题解析
14. 已知一组数据 $- 1$ ，x ， 0，1， $- 2$ 的平均数是0，那么这组数据的方差是

查看试题解析
15. 如图，任意四边形ABCD各边中点分别是E ， F ， G ， H ，若对角线AC ， BD的长都为10 cm ，则四边形EFGH的周长是cm ．

查看试题解析
16. 如图，小明用三个等腰三角形（图中①②③）拼成了一个平行四边形ABCD，且 $∠ D > 90 ° > ∠ C$ ，则 $∠ C$ = 度

查看试题解析

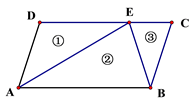
三、解答题

17. 计算：

(1)、 ${(- \sqrt{6})}^{2} - \sqrt{25} + \sqrt{{(- 3)}^{2}}$

(2)、 $\sqrt{3} (\sqrt{2} - \sqrt{3}) - \sqrt{24} - | \sqrt{6} - 3 |$

查看试题解析
18. 用适当的方法解下列一元二次方程：

(1)、 $x^{2} = 2 x$

(2)、 $x^{2} - 4 x + 1 = 0$

查看试题解析
19. 八（2）班组织了一次经典朗读比赛，甲、乙两队各10人的比赛成绩如下表（10分制）：
甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9

(1)、甲队成绩的中位数是分，乙队成绩的众数是分；

(2)、计算乙队的平均成绩和方差；

(3)、已知甲队成绩的方差是1.4分² ，则成绩较为整齐的是队．

查看试题解析
20. 已知关于x的方程 $x^{2} + 2 x + a - 2 = 0$ .

(1)、若该方程有两个不相等的实数根，求实数a的取值范围；

(2)、若该方程的一个根为1，求a的值及该方程的另一根.

查看试题解析
21. 图1、图2是两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1，每个小正方形的顶点叫做格点．

(1)、在图1中画出等腰直角三角形MON ，使点N在格点上，且∠MON=90°；

(2)、在图2中以格点为顶点画一个平行四边形ABCD ，使平行四边形ABCD面积等于（1）中等腰直角三角形MON面积的4倍（画出一种即可）．

查看试题解析
22. 某厂生产一种旅行包，每个旅行包的成本为40元，出厂单价定为60元，该厂为鼓励销售商订购，决定当一次订购量超过100个时，每多订一个，订购的全部旅行包的出厂单价就降低0.02元．根据市场调查，销售商一次订购量不会超过550个．

(1)、设销售商一次订购量为x个，旅行包的实际出厂单价为y元，写出当一次订购量超过100个时，y与x的函数关系式；

(2)、求当销售商一次订购多少个旅行包时，可使该厂获得利润6000元？（售出一个旅行包的利润＝实际出厂单价－成本）

查看试题解析
23. 如图，平行四边形ABCD中，AE平分∠BAD ，交BC于点E ，且AB=AE ，延长AB与DE的延长线交于点F ．下列结论中：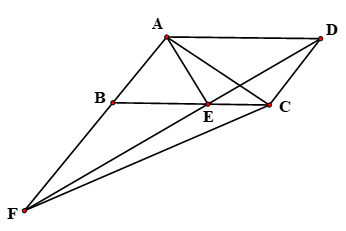

求证：

(1)、△ABE是等边三角形；

(2)、△ABC≌△EAD；

(3)、 $S_{△ A B E} = S_{△ C E F}$ ．

查看试题解析
24. 我们知道平行四边形有很多性质. 如果我们把平行四边形沿着它的一条对角线翻折，那么会发现这其中还有更多的结论.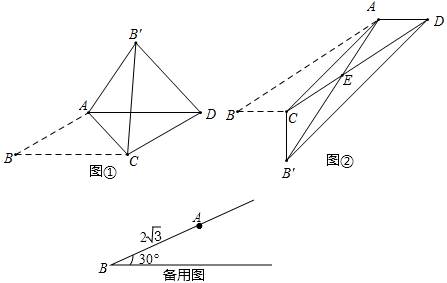

(1)、发现与证明：

在▱ABCD中， $A B \neq B C$ ，将 $△ A B C$ 沿AC翻折至 $△ A B^{'} C$ ，连接 $B^{'} D$ .

结论1： $B^{'} D$ //AC；

结论2： $△ A B^{'} C$ 与▱ABCD重叠部分的图形是等腰三角形.

请利用图①证明结论1或结论2（只需证明一个结论）.

(2)、应用与探究：

在▱ABCD中，已知∠B=30°，将 $△ A B C$ 沿AC翻折至 $△ A B^{'} C$ ，连接 $B^{'} D$ .
如图①，若 $A B = \sqrt{3} ， ∠ A B^{'} D = 75 °$ ，则∠ACB= °，BC= ；

(3)、如图②， $A B = 2 \sqrt{3}$ ，BC=1， $A B^{'}$ 与边CD相交于点E，求 $△ A E C$ 的面积；

(4)、已知 $A B = 2 \sqrt{3}$ ，当BC长为多少时， $∠ B^{'} A D = 90 °$ ？

查看试题解析

甲	7	8	9	7	10	10	9	10	10	10
乙	10	8	7	9	8	10	10	9	10	9