浙江省舟山市普陀区重点达标名校2021年数学中考适应性试卷

试卷更新日期：2021-05-11 类型：中考模拟

进入出卷网下载

一、单选题

1. 甲骨文是我国的一种古代文字，是汉字的早期形式，下列甲骨文中，不是轴对称的是（　　）

A、 B、 C、 D、

查看试题解析
2. 定义：一个自然数，右边的数字总比左边的数字小，我们称之为“下滑数”(如：32，641，8531等).现从两位数中任取一个，恰好是“下滑数”的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{7}{18}$

查看试题解析
3. 如图，按照三视图确定该几何体的侧面积是(单位：cm)（）

A、24π cm² B、48π cm² C、60π cm² D、80π cm²

查看试题解析
4. △ABC在网络中的位置如图所示，则cos∠ACB的值为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
5. 如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧交AB于M、AC于N，再分别以M、N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧交于点P，连接AP并延长交BC于D，下列四个结论：①AD是∠BAC的平分线；②∠ADC=60°；③点D在AB的中垂线上；④S_△_ACD：S_△_ACB=1：3．其中正确的有（）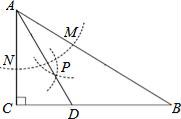

A、只有①②③ B、只有①②④ C、只有①③④ D、①②③④

查看试题解析
6. 如图，在菱形ABCD中，M，N分别在AB，CD上，且AM＝CN，MN与AC交于点O，连接BO.若∠DAC＝26°，则∠OBC的度数为（）

A、54° B、64° C、74° D、26°

查看试题解析
7. 如图，数轴上表示的是下列哪个不等式组的解集（）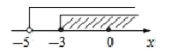

A、 ${\begin{array}{l} x \geq - 5 \\ x > - 3 \end{array}$ B、 ${\begin{array}{l} x > - 5 \\ x \geq - 3 \end{array}$ C、 ${\begin{array}{l} x < 5 \\ x < - 3 \end{array}$ D、 ${\begin{array}{l} x < 5 \\ x > - 3 \end{array}$

查看试题解析
8. 如图是抛物线y=ax²+bx+c（a≠0）的图象的一部分，抛物线的顶点坐标是A（1，4），与x轴的一个交点是B（3，0），下列结论：①abc＞0；②2a+b=0；③方程ax²+bx+c=4有两个相等的实数根；④抛物线与x轴的另一个交点是（﹣2.0）；⑤x（ax+b）≤a+b，其中正确结论的个数是（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
9. 如图，菱形ABCD的对角线相交于点O，过点D作DE∥AC，且DE= $\frac{1}{2}$ AC，连接CE，OE，连接AE，交OD于点F．若AB=2，∠ABC=60°，则AE的长为（）

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、 $\sqrt{7}$ D、 $2 \sqrt{2}$

查看试题解析
10. 如图是棋盘的一部分，建立适当的平面直角坐标系，已知棋子“车”的坐标为（-2，1），棋子“马”的坐标为（3，-1），则棋子“炮”的坐标为（）

A、（1，1） B、（2，1） C、（2，2） D、（3，1）

查看试题解析
11. sin60°=（　　）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、1 D、 $\frac{\sqrt{3}}{2}$

查看试题解析
12. 如图，正方形被分割成四部分，其中I、II为正方形，III、IV为长方形，I、II的面积之和等于III、IV面积之和的2倍，若II的边长为2，且I的面积小于II的面积，则I的边长为（）

A、4 B、3 C、 $4 - 2 \sqrt{3}$ D、 $4 + 2 \sqrt{3}$

查看试题解析

二、填空题

13. 某校组织“优质课大赛”活动，经过评比有两名男教师和两名女教师获得一等奖，学校将从这四名教师中随机挑选两位教师参加市教育局组织的决赛，挑选的两位教师恰好是一男一女的概率为．

查看试题解析
14. 函数 $y = \frac{x}{1 - x}$ 的自变量 $x$ 的取值范围是.

查看试题解析
15. 如图，在Rt△ABC中，∠ACB=90°，将边BC沿斜边上的中线CD折叠到CB′，若∠B=48°，则∠ACB′= ．

查看试题解析
16. 如图，是由大小完全相同的正六边形组成的图形，小军准备用红色、黄色、蓝色随机给每个正六边形分别涂上其中的一种颜色，则上方的正六边形涂红色的概率是．

查看试题解析
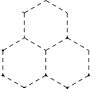17. 如图（1），将一个正六边形各边延长，构成一个正六角星形 $A F B D C E$ ，它的面积为1；取 $△ A B C$ 和 $△ D E F$ 各边中点，连接成正六角星形 $A_{1} F_{1} B_{1} D_{1} C {}_{1}E_{1}$ ，如图（2）中阴影部分；取 $△ A_{1} B_{1} C_{1}$ 和 $△ D_{1} E_{1} F_{1}$ 各边中点，连接成正六角星形 $A_{2} F_{2} B_{2} D_{2} C {}_{2}E_{2}$ ，如图（3）中阴影部分；如此下去……，则正六角星形 $A_{4} F_{4} B_{4} D_{4} C_{4} E_{4}$ 的面积为 .

查看试题解析
18. 如图，“人字梯”放在水平的地面上，当梯子的一边与地面所夹的锐角 $α$ 为 $60^{\circ}$ 时，两梯角之间的距离BC的长为 $3 m .$ 周日亮亮帮助妈妈整理换季衣服，先使 $α$ 为 $60^{\circ}$ ，后又调整 $α$ 为 $45^{\circ}$ ，则梯子顶端离地面的高度AD下降了 $m ($ 结果保留根号 $)$ .

查看试题解析

三、解答题

19. 如图，抛物线 $y = - {(x - 1)}^{2} + c$ 与 $x$ 轴交于 $A$ ， $B$ （ $A$ ， $B$ 分别在 $y$ 轴的左右两侧）两点，与 $y$ 轴的正半轴交于点 $C$ ，顶点为 $D$ ，已知 $A (- 1 ， 0)$ .

(1)、求点 $B$ ， $C$ 的坐标；

(2)、判断 $△ C D B$ 的形状并说明理由；

(3)、将 $△ C O B$ 沿 $x$ 轴向右平移 $t$ 个单位长度 $(0 < t < 3)$ 得到 $△ Q P E$ . $△ Q P E$ 与 $△ C D B$ 重叠部分（如图中阴影部分）面积为 $S$ ，求 $S$ 与 $t$ 的函数关系式，并写出自变量 $t$ 的取值范围.

查看试题解析
20. 如图，二次函数 $y = - x^{2} + 3 x + m$ 的图象与x轴的一个交点为 $B (4 ， 0)$ ，另一个交点为A，且与y轴相交于C点

(1)、求m的值及C点坐标；

(2)、在直线BC上方的抛物线上是否存在一点M，使得它与B，C两点构成的三角形面积最大，若存在，求出此时M点坐标；若不存在，请简要说明理由

(3)、P为抛物线上一点，它关于直线BC的对称点为Q
$①$ 当四边形PBQC为菱形时，求点P的坐标；

$②$ 点P的横坐标为 $t (0 < t < 4)$ ，当t为何值时，四边形PBQC的面积最大，请说明理由.

查看试题解析
21. 如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．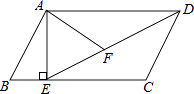

(1)、求证：△ADF∽△DEC；

(2)、若AB=8，AD=6 $\sqrt{3}$ ，AF=4 $\sqrt{3}$ ，求AE的长．

查看试题解析
22. 有 $A$ ， $B$ 两个黑布袋， $A$ 布袋中有两个完全相同的小球，分别标有数字1和1， $B$ 布袋中有三个完全相同的小球，分别标有数字－1，－1和－2，小明从 $A$ 布袋中随机取出一个小球，记录其标有的数字为 $x$ ，再从 $B$ 布袋中随机取出一个小球，记录其标有的数字为 $y$ ，这样就确定点 $Q$ 的一个坐标为 $(x, y)$ .

(1)、用列表或画树状图的方法写出点 $Q$ 的所有可能坐标；

(2)、求点 $Q$ 落在直线 $y = - x - 1$ 上的概率.

查看试题解析
23. 已知：如图1，抛物线的顶点为 $M$ ，平行于 $x$ 轴的直线与该抛物线交于点 $A$ ， $B$ （点 $A$ 在点 $B$ 左侧），根据对称性 $△ A M B$ 恒为等腰三角形，我们规定：当 $△ A M B$ 为直角三角形时，就称 $△ A M B$ 为该抛物线的“完美三角形”.

(1)、①如图2，求出抛物线 $y = x^{2}$ 的“完美三角形”斜边 $A B$ 的长；
②抛物线 $y = x^{2} + 1$ 与 $y = x^{2}$ 的完美三角形的斜边长的数量关系是 ▲ ；

(2)、若抛物线 $y = a x^{2} + 4$ 的“完美三角形”的斜边长为4，求 $a$ 的值；

(3)、若抛物线 $y = m x^{2} + 2 x + n - 5$ 的“完美三角形”斜边长为 $n$ ，且 $y = m x^{2} + 2 x + n - 5$ 的最大值为1，求 $m$ ， $n$ 的值.

查看试题解析
24. 如图，某校数学兴趣小组要测量大楼AB的高度，他们在点C处测得楼顶B的仰角为30°，再往大楼AB方向前进至点D处测得楼顶B的仰角为48°，CD＝96m，其中点A、D、C在同一直线上.求AD的长和大楼AB的高度（结果精确到1m）参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11， $\sqrt{3}$ ≈1.73.

查看试题解析
25. 某市出租车计费方法如图所示，x(km)表示行驶里程，y(元)表示车费，请根据图象回答下列问题：

(1)、出租车的起步价是多少元？当x＞3时，求y关于x的函数关系式；

(2)、若某乘客有一次乘出租车的车费为32元，求这位乘客乘车的里程.

查看试题解析
26. 如图，在△ABC中，AB=AC，∠BAC=120°，EF为AB的垂直平分线，交BC于点F，交AB于点E．求证：FC=2BF．

查看试题解析
27. 发现：如图1，在有一个“凹角 $∠ A_{1} A_{2} A_{3}$ ” $n$ 边形 $A_{1} A_{2} A_{3} A_{4}$ … $A_{n}$ 中（ $n$ 为大于3的整数）， $∠ A_{1} A_{2} A_{3} = ∠ A_{1} + ∠ A_{3} + ∠ A_{4} + ∠ A_{5} + ∠ A_{6} + \dots \dots + ∠ A_{n} - (n - 4) \times 180 °$ .
验证：

(1)、如图2，在有一个“凹角 $∠ A B C$ ”的四边形 $A B C D$ 中，证明： $∠ A B C = ∠ A + ∠ C + ∠ D$ .

(2)、如图3，有一个“凹角 $∠ A B C$ ”的六边形 $A B C D E F$ 中，证明； $∠ A B C = ∠ A + ∠ C + ∠ D + ∠ E + ∠ F - 360 °$ .
延伸：

(3)、如图4，在有两个连续“凹角 $A_{1} A_{2} A_{3}$ 和 $∠ A_{2} A_{3} A {}_{4}$ ”的四边形 $A_{1} A_{2} A_{3} A_{4}$ …… $A_{n}$ 中（ $n$ 为大于4的整数）， $∠ A_{1} A_{2} A_{3} + ∠ A_{2} A_{3} A_{4} = ∠ A_{1} + ∠ A_{4} + ∠ A_{5} + ∠ A_{6 \dots ..} + ∠ A_{n} -$ （n-） $\times 180 °$ .

查看试题解析