浙江省杭州市滨江区2021年九年级下学期数学中考一模试卷

试卷更新日期：2021-05-11 类型：中考模拟

进入出卷网下载

一、单选题

1. $| - 7 | =$ （）

A、-7 B、7 C、±7 D、49

查看试题解析
2. 数据1900000科学记数法表示为（）

A、 ${1.9}^{6}$ B、 $1.9 \times 10^{6}$ C、 $1.9 \times 10^{5}$ D、 $19 \times 10^{6}$

查看试题解析
3. 下列因式分解中正确的是（）

A、 $m^{2} + n^{2} = (m + n) (m - n)$ B、 $- 3 x - 6 = - 3 (x - 2)$ C、 $a^{2} - a = a (a - 1)$ D、 $a^{2} + a + 1 = a (a + 1) + 1$

查看试题解析
4. 若点 $A (m, 2)$ 与点 $B (- 1, n)$ 关于y轴对称，则 $m + n =$ （）

A、-3 B、-1 C、1 D、3

查看试题解析
5. 若 $x > y$ ，则（）

A、 $2 x < 2 y$ B、 $x > y + 1$ C、 $- 2 x - 2 < - 2 y - 2$ D、 $x - 1 < y - 1$

查看试题解析
6. 某女子排球队6名场上队员身高（单位： $cm$ ）是：170，174，178，180，180，184，现用身高为 $178 cm$ 的队员替换下场上身高为 $174 cm$ 的队员，与换人前相比，场上队员的身高（）.

A、平均数变大，中位数不变 B、平均数变大，中位数变大 C、平均数变小，中位数不变 D、平均数变小，中位数变大

查看试题解析
7. 已知，如图，线段 $A B$ 是 $⊙ O$ 的直径，弦 $C D ⊥ A B$ 于点E.若 $A E = 2$ ， $C D = 6$ ，则 $O B$ 的长度为（）

A、 $\sqrt{13}$ B、 $\frac{13}{4}$ C、 $\frac{13}{2}$ D、5

查看试题解析
8. 下列命题中，（）
①底边和顶角对应相等的两个等腰三角形全等②对角线相等的四边形是矩形

A、①正确②正确 B、①正确②错误 C、①错误②正确 D、①错误②错误

查看试题解析
9. 一个门框的尺寸如图所示，下列长×宽型号（单位：m）的长方形薄木板能从门框内通过的是（）

A、 $2.9 \times 2.2$ B、 $2.8 \times 2.3$ C、 $2.7 \times 2.4$ D、 $2.6 \times 2.5$

查看试题解析
10. 已知函数 $y = x^{2} - 4 a x + 5$ （a为常数），当 $x ⩾ 4$ 时，y随x增大而增大. $P (x_{1}, y_{1}), Q (x_{2}, y_{2})$ 是该函数图象上的两点，对任意的 $2 a - 1 ⩽ x_{1} ⩽ 5$ 和 $2 a - 1 ⩽ x_{2} ⩽ 5$ ， $y_{1}, y_{2}$ 总满足 $y_{1} - y_{2} ⩽ 5 + 4 a^{2}$ ，则实数a的取值范围是（）

A、 $- 1 ⩽ a ⩽ 2$ B、 $1 ⩽ a ⩽ 2$ C、 $2 ⩽ a ⩽ 3$ D、 $2 ⩽ a ⩽ 4$

查看试题解析

二、填空题

11. 如图， $a / / b$ ，若 $∠ 1 = 58 °$ ，则 $∠ 2 =$ .

查看试题解析
12. 已知函数 $y = \frac{m}{x}$ （m为常数， $m \neq 0$ ），在图象所在的每一象限内y随x的增大而增大，则m的取值范围是.

查看试题解析
13. 已知 $a + b = 3, a - b = 1$ ，则 $a^{2} + b^{2} =$ .

查看试题解析
14. 从 $- 2$ ，3中任取一个数，再从0， $- 1$ ，4中任取一个数，则所取两个数的乘积为负数的概率是.

查看试题解析
15. 如图，若 $∠ C A B = 30 °$ ， $A E = 1$ ， $E F = 3$ ， $A D = 2$ ，则 $E D^{2} + F D^{2} =$ .

查看试题解析
16. 已知，矩形 $A B C D$ 中， $A B = 6 ， B C = 9$ ，点F在 $A B$ 边上，且 $A F = 2$ ，点E是 $B C$ 边上的一个点，连接 $E F$ ，作线段 $E F$ 的垂直平分线 $H G$ ，分别交边 $A D$ ， $B C$ 于点H、G，连接 $F H$ ， $E H$ .当点E和点C重合时（如图1）， $D H =$ ；当点B，M，D三点共线时（如图2）， $D H =$ .

查看试题解析

三、解答题

17.

(1)、计算： $\frac{1}{2} - \frac{2}{3}$ .

(2)、解方程： $\frac{1}{2 x} - \frac{2}{3 x} = 1$

查看试题解析
18. 进入夏季，为了解某品牌电风扇销售量的情况，厂家对某商场7月份该品牌甲、乙、丙三种型号的电风扇销售量进行统计，绘制如下两个统计图（均不完整）.请你结合图中的信息，解答下列问题：

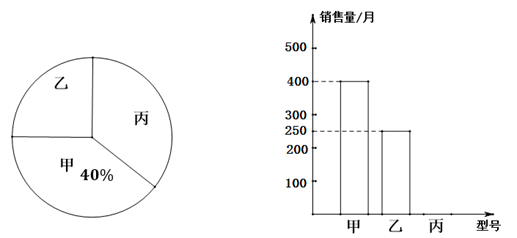(1)、该商场7月份售出这种品牌三种型号的电风扇共多少台？补全条形统计图.

(2)、若该商场计划订购这三种型号的电风扇共5000台，根据7月份销售量的情况，求该商场应订购丙种型号电风扇多少台比较合理？

查看试题解析
19. 已知，如图， $△ A B C$ 中，线段 $A E ， A F ， A B ， A C$ 满足 $A E \cdot A C = A F \cdot A B$ .

(1)、求证： $△ A B C ∽ △ A E F$ .

(2)、若 $A C = 6 ， B C = 5 ， E F = C F$ ，求 $A F$ 的长.

查看试题解析
20. 在平面直角坐标系中，一次函数 $y = k x + b$ （k，b都是常数，且 $k \neq 0$ ）的图象经过点 $(1, 0)$ 和 $(0, - 1)$

(1)、当 $- 1 < x ⩽ 2$ 时，求y的取值范围.

(2)、已知点 $P (m, n)$ 在该函数的图象上，且 $m + n = 5$ ，求点P的坐标.

查看试题解析
21. 如图，矩形 $A B C D$ 中，点E为 $B C$ 边上一点，把 $△ A B E$ 沿着 $A E$ 折叠得到 $△ A E F$ ，点F落在 $A D$ 边的上方，线段 $E F$ 与 $A D$ 边交于点G.

(1)、求证： $△ A G E$ 是等腰三角形

(2)、试写出线段 $F G$ ， $G D$ ， $E C$ 三者之间的数量关系式（用同一个等式表示），并证明.

查看试题解析
22. 某位同学做实验考察电流变化情况时，可以选择若干定值电阻进行并联（假设可以选择仼何数值的电阻），已知电源电压U为 $3V$ （注：公式 $I = \frac{U}{R}$ ，其中I是电流强度、U是电压，R是电阻）

(1)、若只选择一个电阻，测得电流强度I为 $0 .1A$ ，求该电阻R的值.

(2)、若所选的两个电阻分别为 $R_{1}, R_{2}$ ，且 $R_{1} + R_{2} = 20 Ω$ ，恰好使总电流强度I最小，求对应电阻 $R_{1}, R_{2}$ 的值.（注并联时总电阻 $R = \frac{R_{1} \cdot R_{2}}{R_{1} + R_{2}}$ ）（在求对应 $R_{1}, R_{2}$ 的值时，用数学的方法书写过程）

查看试题解析
23. 已知，如图， $△ A B C$ 内接于 $⊙ O$ ，边 $B C$ 为直径，且 $A C = 3 ， A B = 4$ .点P是直径 $B C$ 下方圆弧上一点， $A P$ 与 $B C$ 交于点Q.

(1)、求 $⊙ O$ 的半径.

(2)、当 $\overset{⌢}{B P} = \overset{⌢}{C P}$ ，求 $A P$ 的长度.

(3)、若 $\frac{P Q}{A Q} = \frac{5}{6}$ ，求弦 $B P$ 的长度.

查看试题解析