湖北省武汉市四校2021年数学中考模拟联考试卷（4月）

试卷更新日期：2021-05-11 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列图案中是中心对称图形但不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. “翻开数学书，恰好翻到第16页”，这个事件是（）

A、随机事件 B、必然事件 C、不可能事件 D、确定事件

查看试题解析
3. 已知 $x_{1}, x_{2}$ 是关于 $x$ 的一元二次方程 $x^{2} - (5 m - 6) x + m^{2} = 0$ 的两个不相等的实根，且满足 $x_{1} + x_{2} = m^{2}$ ，则 $m$ 的值是（）

A、2 B、3 C、2或3 D、-2或-3

查看试题解析
4. 已知点P的坐标是（﹣6，5），则P点关于原点的对称点的坐标是（　　）

A、（﹣6，﹣5） B、（6，5） C、（6，﹣5） D、（5，﹣6）

查看试题解析
5. 抛物线y＝x²﹣9的顶点坐标是（）

A、（0，﹣9） B、（﹣3，0） C、（﹣9，0） D、（3，0）

查看试题解析
6. 如图，小球从A口往下落，在每个交叉口都有向左或向右两种可能，且可能性相同，则小球最终从E口落出的概率为（）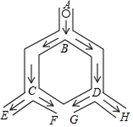

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{1}{8}$

查看试题解析
7. 如图，为了测量某棵树的高度，小明用长为2m的竹竿做测量工具，移动竹竿，使竹竿、树的顶端的影子恰好落在地面的同一点.此时，竹竿与这一点距离相距6m，与树相距15m，则树的高度是（）

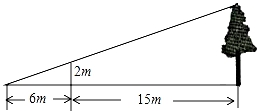A、7m B、6m C、5m D、4m

查看试题解析
8. 如图， $△ A B C$ 中， $C D ⊥ A B$ 于D，下列条件中：① $∠ 1 = ∠ A$ ；② $\frac{C D}{A D} = \frac{D B}{C D}$ ；③ $∠ B + ∠ 2 = 90 °$ ；④ $∠ B A C ： ∠ A B C ： ∠ A C B = 3 ： 4 ： 5$ ；⑤ $A C \cdot B D = A D \cdot C D$ ，⑥ $∠ 1 + ∠ 2 = ∠ A + ∠ B$ ，一定能确定 $△ A B C$ 为直角三角形的条件的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
9. 函数 $y_{1} = \frac{6}{x}$ 和函数y₂＝x，则关于函数y＝y₁+y₂的结论正确的是（）

A、函数的图象关于原点中心对称 B、当x＞0时，y随x的增大而减小 C、当x＞0时，函数的图象最低点的坐标是（1，6） D、函数恒过点（2，4）

查看试题解析
10. 如图，在Rt△ABO中，AB⊥OB，且AB=OB=3，设直线x=t截此三角形所得的阴影部分的面积为S，则S与t之间的函数关系式为（）

A、S=t(0＜t≤3) B、S= $\frac{1}{2}$ t²(0＜t≤3) C、S=t²(0＜t≤3) D、S= $\frac{1}{2}$ t²-1(0＜t≤3)

查看试题解析

二、填空题

11. 算术平方根等于本身的实数是.

查看试题解析
12. 已知反比例函数y＝ $\frac{m - 4}{x}$ 在每个象限内y随x增大而减小，则m的取值范围是.

查看试题解析
13. 某商场八月份的营业额是100万元，预计十月份的营业额可达到144万元，若九、十月份营业额的月增长率相同为 $x$ ，那么由题意可列得方程为

查看试题解析
14. 如图，AB⊥BC，DC⊥BC，点E在BC上，AE⊥DE，DC＝1，BE＝3，BC＝5，则AB＝.

查看试题解析
15. 二次函数y＝ax²＋bx＋c（a≠0）的部分图象如图，图象过点（﹣1，0），对称轴为直线x＝2，下列结论：①4a＋b＝0；②9a＋c＞3b；③4a＋2b≥am²＋bm（m为任意实数）；④当x＞﹣1时，y的值随x值的增大而增大；其中正确的结论有（填序号）.

查看试题解析
16. 如图，△ABO为等边三角形，OA＝6，动点C在以点O为圆心，OA为半径的⊙O上，点D为BC中点，连接AD，则线段AD长的最小值为.

查看试题解析

三、解答题

17. 解方程：2x²﹣5x+1=0

查看试题解析
18. 如图，反比例函数 $y = \frac{k}{x}$ 的图象与一次函数 $y = - \frac{1}{2} x$ 的图象分别交于M，N两点，已知点M(-2，m).

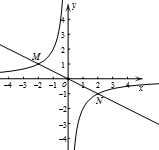(1)、求反比例函数的表达式；

(2)、点P为y轴上的一点，当∠MPN为直角时，直接写出点P的坐标.

查看试题解析
19. 如图，BE，CD是 $△ A B C$ 的高，连接DE.

(1)、求证： $A E \cdot A C = A B \cdot A D$ ；

(2)、若 $∠ B A C = 120 °$ ，M为BC的中点，连接DM.求证： $D E = D M$ .

查看试题解析
20. 图①、图②、图③都是4×4的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点叫做格点，线段AB的端点在格点上，在图①、图②、图③中，只用无刻度的直尺，按下列要求画图，所画图形的顶点均在格点上，只保留作图痕迹，不要求写出画法.

(1)、在图①中以AB为边画一个钝角三角形ABC，使tan∠CAB＝ $\frac{1}{3}$ ；

(2)、在图②中以AB为边画一个Rt△ABD，使tan∠DAB＝1；

(3)、在图③中以AB为边画一个△ABE，使tan∠AEB＝ $\frac{3}{4}$ .

查看试题解析
21. 已知：如图，在△ABC中，AB＝AC，AE是∠BAC的平分线，BM平分∠ABC交AE于点M，经过B，M两点的⊙O交BC于点G，交AB于点F，FB恰为⊙O的直径.

(1)、求证：AE与⊙O相切；

(2)、当BC＝6，cosC＝ $\frac{1}{3}$ 时，求⊙O的半径.

查看试题解析
22. 深圳某百果园店售卖赣南脐橙，已知每千克脐橙的成本价为 $6$ 元，在销售脐橙的这 $40$ 天时间内，销售单价 $x$ （元/千克）与时间第 $t$ （天）之间的函数关系式为 $x = \frac{1}{4} t + 16$ （ $1 \leq t \leq 40$ ，且 $t$ 为整数），日销售量 $y$ （千克）与时间第 $t$ （天）之间的函数关系式为 $y = - 2 t + 200$ （ $1 \leq t \leq 40$ ，且 $t$ 为整数）

(1)、请你直接写出日销售利润 $w$ （元）与时间第 $t$ （天）之间的函数关系式；

(2)、该店有多少天日销售利润不低于 $2400$ 元？

(3)、在实际销售中，该店决定每销售 $1$ 千克脐橙，就捐赠 $m (m < 7)$ 元给希望工程，在这 $40$ 天中，每天扣除捐赠后的日销售利润随时间 $t$ 的增大而增大，求 $m$ 的取值范围．

查看试题解析
23. 点E是矩形ABCD边AB延长线上的一动点，在矩形ABCD外作Rt△ECF，其中∠ECF＝90°，过点F作FG⊥BC，交BC的延长线于点G，连接DF，交CG于点H.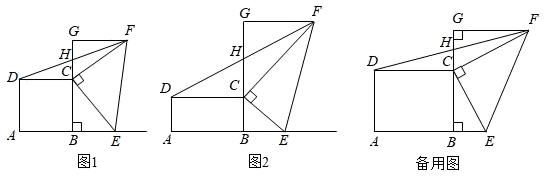

(1)、发现：如图1，若AB＝AD，CE＝CF，猜想线段DH与HF的数量关系是；

(2)、探究：如图2，若AB＝nAD，CF＝nCE，则（1）中的猜想是否仍然成立？若成立，请给予证明；若不成立，请说明理由.

(3)、拓展：在（2）的基础上，若射线FC过AD的三等分点，AD＝3，AB＝4，则直接写出线段EF的长.

查看试题解析
24. 如图，在平面直角坐标系中，抛物线y＝﹣x²＋bx＋c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点 C.

(1)、直接写出抛物线的解析式为：；

(2)、点D为第一象限内抛物线上的一动点，作DE⊥x轴于点E，交BC于点F，过点F作BC的垂线与抛物线的对称轴和y轴分别交于点G，H，设点D的横坐标为m.
①求DF＋HF的最大值；

②连接EG，若∠GEH＝45°，求m的值.

查看试题解析