河南省开封市2021年九年级下学期数学中考一模试卷
试卷更新日期:2021-05-11 类型:中考模拟
一、单选题
-
1. 下列各数中,最小的数是( )A、2 B、0 C、-1 D、2. 2021年清明文化节期间,古城开封累计接待游客121.76万人次,与2019年同期相比增长 ;实现综合收入5.27亿元,同比增长 ,数据121.76万用科学记数法表示为( )A、 B、 C、 D、3. “疫情就是命令,防控就是责任”,面对疫情,各地积极普及科学防控知识.下面是科学防控知识图片,其中图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图是由几个小立方块所搭成的几何体的俯视图,小正方形中的数字表示在该方块的个数,则这个几何体的左视图为( )
4. 如图是由几个小立方块所搭成的几何体的俯视图,小正方形中的数字表示在该方块的个数,则这个几何体的左视图为( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,直线 相交于点 于点 平分 ,则下列结论中不正确的是( )
5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,直线 相交于点 于点 平分 ,则下列结论中不正确的是( ) A、 B、 C、 与 互为补角 D、 的余角等于7. 定义运算: .例如: .则方程 的根的情况为( )A、无实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根8. 如图,在 中,分别以点A和点C为圆心,大于 的长为半径作弧,两弧相交于 两点,作直线 ,交 于点 的周长为13,则 的周长是( )
A、 B、 C、 与 互为补角 D、 的余角等于7. 定义运算: .例如: .则方程 的根的情况为( )A、无实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根8. 如图,在 中,分别以点A和点C为圆心,大于 的长为半径作弧,两弧相交于 两点,作直线 ,交 于点 的周长为13,则 的周长是( ) A、16 B、17 C、18 D、199. 如图,在平面直角坐标系 中,将四边形 先向上平移,再向左平移得到四边形 ,已知 ,则点B坐标为( )
A、16 B、17 C、18 D、199. 如图,在平面直角坐标系 中,将四边形 先向上平移,再向左平移得到四边形 ,已知 ,则点B坐标为( ) A、 B、 C、 D、10. 小明周末前往游乐园游玩,他乘坐了摩天轮,摩天轮转一圈,他离地面高度 与旋转时 之间的关系可以近似地用 来刻画.如图记录了该摩天轮旋转时 和离地面高度 的三组数据,根据上述函数模型和数据,可以推断出:当小明乘坐此摩天轮离地面最高时,需要的时间为( )
A、 B、 C、 D、10. 小明周末前往游乐园游玩,他乘坐了摩天轮,摩天轮转一圈,他离地面高度 与旋转时 之间的关系可以近似地用 来刻画.如图记录了该摩天轮旋转时 和离地面高度 的三组数据,根据上述函数模型和数据,可以推断出:当小明乘坐此摩天轮离地面最高时,需要的时间为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 一元二次方程x2=x的解为 .12. 经过某十字路口的汽车,可直行,也可向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过该十字路口时都直行的概率是 .13. 如图数轴上两点 表示的数分别是 ,点C在数轴上,若 ,则点C表示的数为.
 14. 如图,在平面直角坐标中,一次函数y=﹣4x+4的图象与x轴、y轴分别交于A、B两点.正方形ABCD的顶点C、D在第一象限,顶点D在反比例函数 (k≠0)的图象上.若正方形ABCD向左平移n个单位后,顶点C恰好落在反比例函数的图象上,则n的值是.
14. 如图,在平面直角坐标中,一次函数y=﹣4x+4的图象与x轴、y轴分别交于A、B两点.正方形ABCD的顶点C、D在第一象限,顶点D在反比例函数 (k≠0)的图象上.若正方形ABCD向左平移n个单位后,顶点C恰好落在反比例函数的图象上,则n的值是.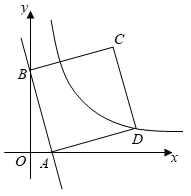 15. 如图,扇形 中, ,点C是 上的一个定点(不与 重合),点 分别是 上的动点,则 周长的最小值为.
15. 如图,扇形 中, ,点C是 上的一个定点(不与 重合),点 分别是 上的动点,则 周长的最小值为.
三、解答题
-
16. 下面是某同学进行分式化简的过程,请认真阅读并完成相应的任务.
分式化简:
解:原式= 第一步
第二步
第三步
第四步
第五步
任务一:填空:第_▲_步开始出现错误,这一步错误的原因是_▲_.
任务二:请写出本题化简后的正确结果,并从不等式组 的解集中选取一个合适的整数作为x的值,代入求值.
任务三:请你根据平时的学习经验,就分式的化简时应注意的事项给其他同学提两条建议.
17. 红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛,试卷题目共10题,每题10分.现分别从三个班中各随机取10名同学的成绩(单位:分),收集数据如下:1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
分数
人数
班级
60
70
80
90
100
1班
0
1
6
2
1
2班
1
1
3
1
3班
1
1
4
2
2
分析数据:
平均数
中位数
众数
1班
83
80
80
2班
83
3班
80
80
根据以上信息回答下列问题:
(1)、请直接写出表格中 的值;(2)、比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由;(3)、为了让学生重视安全知识的学习,学校将给竞赛成绩满分的同学颁发奖状,该校七年级新生共570人,试估计需要准备多少张奖状?18. 被誉为“天下第一塔”的开封铁塔,八角十三层,其设计精巧,单是塔砖就有数十种图案,它历经战火、水患、地震等灾害,依然屹立.某数学兴趣小组通过调查研究把“如何测量铁塔的高度”作为一项课题活动,他们制订了测量方案,并利用课余时间实地测量.课题
测量铁塔的高度
测量工具
测量角度的仪器,皮尺等
测量方案
在点C处放置高为1.3米高的测角仪,此时测得塔顶端A的仰角为 ,再沿 方向走20.5米到达点E处,此时测得塔顶端A的仰角为 .
说明:点 三点在同一水平线上.

 (1)、请你根据表中信息帮助该数学兴趣小组求铁塔的高度.
(1)、请你根据表中信息帮助该数学兴趣小组求铁塔的高度.(精确到0.1米,参考数据: )
(2)、景点介绍开封铁塔的高度为55.88米,则计算结果的误差为多少?请你说出一条导致计算结果产生误差的原因可能是什么?19. 如图, 是 的直径,点C为 上一点,点P是半径 上一动点(不与 重合),过点P作射线 ,分别交弦 于 两点,在射线 上取点F,使 . (1)、求证: 是 的切线.(2)、当点E是 的中点时,若 ,判断以 为顶点的四边形是什么特殊四边形,并说明理由.20. 疫情防控期间,某校校医每天早上对全校办公室和教室进行药物喷洒消毒,完成1间办公室和1间教室的喷酒共需 ;完成2间办公室和3教室的喷洒共需 .
(1)、求证: 是 的切线.(2)、当点E是 的中点时,若 ,判断以 为顶点的四边形是什么特殊四边形,并说明理由.20. 疫情防控期间,某校校医每天早上对全校办公室和教室进行药物喷洒消毒,完成1间办公室和1间教室的喷酒共需 ;完成2间办公室和3教室的喷洒共需 . (1)、该校医完成一间办公室和一间教室的药物喷洒各需多少时间?(2)、消毒药物在一间教室内空气中的浓度y(单位: )与时间x(单位: )的函数关系如图所示,校医进行药物喷洒时y与x的函数关系式为 ,药物喷洒完成后y与x成反比例函数关系,两个函数图象的交点为点 .当教室空气中的药物浓度不高于 时,对人体健康无危害,校医依次对(1)班至(11)班教室(共11间)进行药物喷洒消毒,当把最后一间教室药物喷洒完成后,(1)班学生能否进入教室?请通过计算说明.21. 在平面直角坐标系 中, 与x轴的交点为 ,与y轴交于点C.
(1)、该校医完成一间办公室和一间教室的药物喷洒各需多少时间?(2)、消毒药物在一间教室内空气中的浓度y(单位: )与时间x(单位: )的函数关系如图所示,校医进行药物喷洒时y与x的函数关系式为 ,药物喷洒完成后y与x成反比例函数关系,两个函数图象的交点为点 .当教室空气中的药物浓度不高于 时,对人体健康无危害,校医依次对(1)班至(11)班教室(共11间)进行药物喷洒消毒,当把最后一间教室药物喷洒完成后,(1)班学生能否进入教室?请通过计算说明.21. 在平面直角坐标系 中, 与x轴的交点为 ,与y轴交于点C. (1)、求抛物线的对称轴和点C坐标.(2)、横、纵坐标都是整数的点叫做整点.抛物线在点 之间的部分与线段 所围成的区域为图形W(不含边界).
(1)、求抛物线的对称轴和点C坐标.(2)、横、纵坐标都是整数的点叫做整点.抛物线在点 之间的部分与线段 所围成的区域为图形W(不含边界).①当 时,求图形W内的整点个数;
②若图形W内有2个整点,求m的取值范围.
22. 如图,在等腰 中, , . 是线段 上一动点,取 的中点 ,连接 , .
小刚根据学习函数的经验,对线段 , , 的长度之间的关系进行探究.下面是小刚的探究过程,请补充完整:
观察计算:根据点 在线段 上的不同位置,通过取点,画图和测量,得到了 , , 的长度(单位: )的几组值,如表:
位置1
位置2
位置3
位置4
位置5
位置6
位置7
位置8
位置9
0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
6.4
5.5
4.6
3.8
22.5.5
2.2
2.5
3.0
6.0
5.4
4.9
4.6
4.5
4.6
4.9
5.4
6.0
(1)、操作发现:①在 , , 的长度这三个量中,确定的长度为自变量,的长度和的长度分别都为这个自变量的函数.
②当 为 的中点时, 的长是一个固定的值.请求出上表中 的值为.
(2)、描点画图:在同一平面直角坐标系 中,根据(1)表格中的数据,画出所确定的函数图象.(3)、解决问题:直接写出:当 为等腰三角形时,线段 的长度的近似值.(结果保留一位小数)23. 如图:两个菱形 与菱形 的边 在同一条直线上,边长分别为a和b,点C在 上,点M为 的中点. (1)、观察猜想:如图①,线段 与线段 的数量关系是.(2)、拓展探究:如图②, ,将图①中的菱形 绕点B顺时针旋转至图②位置,其他条件不变,连接 ,
(1)、观察猜想:如图①,线段 与线段 的数量关系是.(2)、拓展探究:如图②, ,将图①中的菱形 绕点B顺时针旋转至图②位置,其他条件不变,连接 ,①猜想线段 与线段 的数量关系,并说明理由.
②求出线段 与 所成的最小夹角.
(3)、解决问题:如图③,若将题目中的菱形改为矩形,且 ,请直接写出线段 与线段 的数量关系.