广西北部湾经济区2021年数学中考全真模拟试卷(二)
试卷更新日期:2021-05-11 类型:中考模拟
一、单选题
-
1. -2021的相反数是( )A、2021 B、-2021 C、 D、2. 下列交通指示标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 过度包装既浪费资源又污染环境,据测算如果全国每年减少十分之一的包装纸用量那么能减少 吨二氧化碳的排放量,把 写成原数是( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 某地区元月份连续七天的空气质量指数( )分别为:118,96,60,82,56,69,86.为了反映这七天空气质量的变化情况,最直观的表示方法是( )A、统计表 B、条形统计图 C、扇形统计图 D、折线统计图6. 已知点 在第二象限,则a的取值范围在数轴上表示是( )A、
3. 过度包装既浪费资源又污染环境,据测算如果全国每年减少十分之一的包装纸用量那么能减少 吨二氧化碳的排放量,把 写成原数是( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 某地区元月份连续七天的空气质量指数( )分别为:118,96,60,82,56,69,86.为了反映这七天空气质量的变化情况,最直观的表示方法是( )A、统计表 B、条形统计图 C、扇形统计图 D、折线统计图6. 已知点 在第二象限,则a的取值范围在数轴上表示是( )A、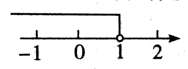 B、
B、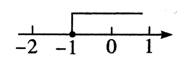 C、
C、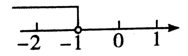 D、
D、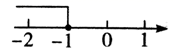 7. 如图,在△ABC中,∠C=90°, ∠A=30°.以点B为圆心画弧,分别交BC、AB于点M、N,再分别以点M、N为圆心,大于 MN为半径画弧,两弧交于点P,画射线BP交AC于点D.若点D到AB的距离为1,则AC的长是( )
7. 如图,在△ABC中,∠C=90°, ∠A=30°.以点B为圆心画弧,分别交BC、AB于点M、N,再分别以点M、N为圆心,大于 MN为半径画弧,两弧交于点P,画射线BP交AC于点D.若点D到AB的距离为1,则AC的长是( )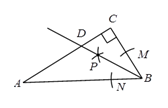 A、2 B、3 C、 D、 +18. 经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过这个十字路口时,一辆向右转,一辆向左转的概率是( )A、 B、 C、 D、9. 某商场在“庆元旦”的活动中将某种服装打折销售,如果每件服装按标价的7折出售将亏20元,而按标价的9折出售将赚40元,则每件服装的标价是( )元.A、200 B、300 C、350 D、40010. 《九章算术》中,有一数学史上有名的测量问题:“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”今译如下:如图,矩形 ,东边城墙 长9里,南边城墙 长7里,东门点 ,南门点 分别位于 , 的中点, , , 里, 经过 点,则 的长为( )
A、2 B、3 C、 D、 +18. 经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过这个十字路口时,一辆向右转,一辆向左转的概率是( )A、 B、 C、 D、9. 某商场在“庆元旦”的活动中将某种服装打折销售,如果每件服装按标价的7折出售将亏20元,而按标价的9折出售将赚40元,则每件服装的标价是( )元.A、200 B、300 C、350 D、40010. 《九章算术》中,有一数学史上有名的测量问题:“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”今译如下:如图,矩形 ,东边城墙 长9里,南边城墙 长7里,东门点 ,南门点 分别位于 , 的中点, , , 里, 经过 点,则 的长为( )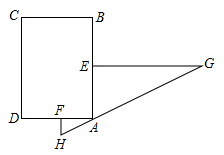 A、0.95里 B、1.05里 C、2.05里 D、2.15里11. 已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB,AC相交于D点,双曲线y= (x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:①双曲线的解析式为y= (x>0);②E点的坐标是(4,8);③sin∠COA= ;④AC+OB=12 ,其中正确的结论有( )
A、0.95里 B、1.05里 C、2.05里 D、2.15里11. 已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB,AC相交于D点,双曲线y= (x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:①双曲线的解析式为y= (x>0);②E点的坐标是(4,8);③sin∠COA= ;④AC+OB=12 ,其中正确的结论有( )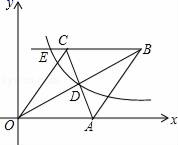 A、1个 B、2个 C、3个 D、4个12. 如图,已知点P(0,3) ,等腰直角△ABC中,∠BAC=90°,AB=AC,BC=2,BC边在x轴上滑动时,PA+PB的最小值是 ( )
A、1个 B、2个 C、3个 D、4个12. 如图,已知点P(0,3) ,等腰直角△ABC中,∠BAC=90°,AB=AC,BC=2,BC边在x轴上滑动时,PA+PB的最小值是 ( )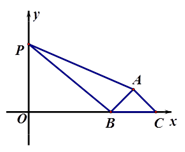 A、 B、 C、5 D、2
A、 B、 C、5 D、2二、填空题
-
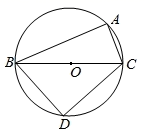
13. 4的算术平方根是 .14. 把x3y﹣xy3分解因式的结果是.15. 若一组数据8,6, ,4,7的平均数是6,则这组数据的方差是.16. 如图, 是 上一点, 是直径, , ,点 在 上且平分 ,则 的长为.
 17. 如图是一根起点为1的数轴,现有同学将它弯折,弯折后虚线上由左至右第1个数是1,第2个数是13,第3个数是41,…,依此规律,第7个数是.
17. 如图是一根起点为1的数轴,现有同学将它弯折,弯折后虚线上由左至右第1个数是1,第2个数是13,第3个数是41,…,依此规律,第7个数是.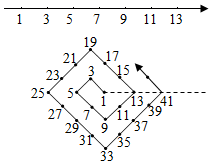 18. 如图①,在 中, ,点E是边 的中点,点P是边 上一动点,设 .图②是y关于x的函数图象,其中H是图象上的最低点..那么 的值为 .
18. 如图①,在 中, ,点E是边 的中点,点P是边 上一动点,设 .图②是y关于x的函数图象,其中H是图象上的最低点..那么 的值为 .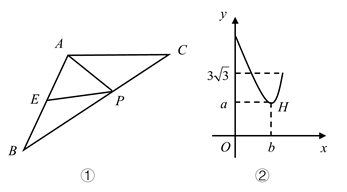
三、解答题
-
19. 计算:20. 解方程组21. 如图, 和 都是等腰直角三角形, , 为 边上一点.
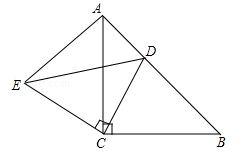 (1)、求证: .(2)、已知 , ,求 的长度.22. 为培养学生良好的运动习惯和运动能力,我校本学期开展了“趣味运动会”和“冬季长跑”等体育活动.为了解七年级学生的长跑水平,我校对全体七年级同学进行了长跑测试,体育组陈老师随机抽取20名男生和20名女生的测试成绩(满分100)进行整理和分析(成绩共分成五组:A. ,B. ,C. ,D. ,E. ),绘制了如下不完整的统计图表:
(1)、求证: .(2)、已知 , ,求 的长度.22. 为培养学生良好的运动习惯和运动能力,我校本学期开展了“趣味运动会”和“冬季长跑”等体育活动.为了解七年级学生的长跑水平,我校对全体七年级同学进行了长跑测试,体育组陈老师随机抽取20名男生和20名女生的测试成绩(满分100)进行整理和分析(成绩共分成五组:A. ,B. ,C. ,D. ,E. ),绘制了如下不完整的统计图表: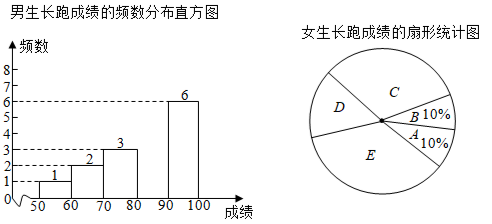
( 1 )收集、整理数据
20名男生的长跑成绩分别为:
76,77,95,88,50,89,89,97,99,93
97,89,65,87,68,89,78,88,98,88
女生长跑成绩在C组和D组的分别为:
73,74,74,74,74,76,83,88,89
( 2 )分析数据:两组样本数据的平均数、中位数和众数如下表所示:
长跑成绩
平均数
中位数
众数
男生
85
88.5
女生
81.8
74
请根据以上信息,回答下列问题:
(1)、①补全频数分布直方图②填空: ▲ , ▲ ;
(2)、根据以上数据,你认为七年级学生是男生的长跑的成绩更好还是女生的长跑成绩更好?判断并说明理由(一条理由即可).(3)、如果我校七年级有男生900名,女生600名,请估计七年级长跑成绩不低于80分的学生人数.23. 为了监控大桥下坡路段车辆行驶速度,通常会在下引桥处设置电子眼进行区间测速,如图,电子眼位于点P处,离地面的铅锤高度PQ为9米,区间测速的起点为下引桥坡面点A处,此时电子眼的俯角为30°;区间测速的中点为下引桥坡脚点B处,此时电子眼的俯角为60°(A、B、P、Q四点在同一平面).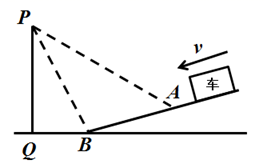 (1)、求路段BQ的长(结果保留根号);(2)、当下引桥坡度 时,求电子眼区间测速路段AB的长(结果保留根号).24. 锦潭社区计划对某区域进行绿化,经投标,由甲、乙两个工程队一起来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的1.5倍,并且在独立完成面积为 区域的绿化时,甲队比乙队少用2天.(1)、求甲、乙两工程队每天各能完成的绿化面积;(2)、若计划绿化的区域面积是 ,甲队每天绿化费用是0.5万元,乙队每天绿化费用为0.3万元.
(1)、求路段BQ的长(结果保留根号);(2)、当下引桥坡度 时,求电子眼区间测速路段AB的长(结果保留根号).24. 锦潭社区计划对某区域进行绿化,经投标,由甲、乙两个工程队一起来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的1.5倍,并且在独立完成面积为 区域的绿化时,甲队比乙队少用2天.(1)、求甲、乙两工程队每天各能完成的绿化面积;(2)、若计划绿化的区域面积是 ,甲队每天绿化费用是0.5万元,乙队每天绿化费用为0.3万元.①当甲、乙各施工几天,既能刚好完成绿化任务,又能使总费用恰好为12.2万元;
②按要求甲队至少施工10天,乙队至多施工22天,当甲乙各施工几天,既能刚好完成绿化任务,又使得总费用最少(施工天数不能是小数)并求最少总费用.
25. 如图,在 中, ,点 在斜边 上,以 为圆心, 为半径作 ,分别与 、 相交于点 、 ,连接 ,已知 .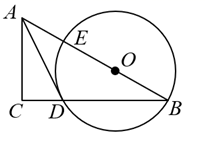 (1)、求证: 是 的切线;(2)、若 , ,求 的长;(3)、若 , ,求 的长.26. 定义:对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x≥0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数.例如:一次函数y=x﹣1,它的相关函数为 .(1)、已知点A(﹣5,8)在一次函数y=ax﹣3的相关函数的图象上,求a的值;(2)、已知二次函数 .
(1)、求证: 是 的切线;(2)、若 , ,求 的长;(3)、若 , ,求 的长.26. 定义:对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x≥0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数.例如:一次函数y=x﹣1,它的相关函数为 .(1)、已知点A(﹣5,8)在一次函数y=ax﹣3的相关函数的图象上,求a的值;(2)、已知二次函数 .①当点B(m, )在这个函数的相关函数的图象上时,求m的值;
②当﹣3≤x≤3时,求函数 的相关函数的最大值和最小值;
(3)、在平面直角坐标系中,点M,N的坐标分别为(﹣ ,1),( ,1),连结MN.直接写出线段MN与二次函数 的相关函数的图象有两个公共点时m的取值范围.