福建省永安市2021年数学初中总复习第一次质量检测试卷
试卷更新日期:2021-05-11 类型:中考模拟
一、单选题
-
1. ( )A、10 B、8 C、7 D、52. 如图是由 个完全相同的小正方体组成的立体图形,它的俯视图是( )
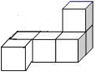 A、
A、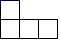 B、
B、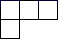 C、
C、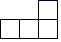 D、
D、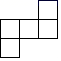 3. 中国的领水面积约为370000km2 , 将数370000用科学记数法表示为( )A、37×104 B、3.7×104 C、0.37×106 D、3.7×1054. 下列计算正确的是( )A、x2+x=x3 B、(﹣3x)2=6x2 C、8x4÷2x2=4x2 D、(x﹣2y)(x+2y)=x2﹣2y25. 下面图形是用数学家名字命名的,其中是中心对称图形但不是轴对称图形的是( )A、
3. 中国的领水面积约为370000km2 , 将数370000用科学记数法表示为( )A、37×104 B、3.7×104 C、0.37×106 D、3.7×1054. 下列计算正确的是( )A、x2+x=x3 B、(﹣3x)2=6x2 C、8x4÷2x2=4x2 D、(x﹣2y)(x+2y)=x2﹣2y25. 下面图形是用数学家名字命名的,其中是中心对称图形但不是轴对称图形的是( )A、 赵爽弦图
B、
赵爽弦图
B、 笛卡尔心形线
C、
笛卡尔心形线
C、 科克曲线
D、
科克曲线
D、 斐波那契螺旋线
6. 已知一个多边形的内角和是540°,则这个多边形是( )A、四边形 B、五边形 C、六边形 D、七边形7. 若 ,其中a为整数,则a的值是( )A、1 B、2 C、3 D、48. 化简 的结果是( )A、a-b B、a+b C、 D、9. 随机调查某市100名普通职工的个人年收入(单位:元)情况,得到这100人年收入的数据,记这100个数据的平均数为a,中位数为b,方差为c.若将其中一名职工的个人年收入数据换成世界首富的年收入数据,则a一定增大,那么对b与c的判断正确的是( )A、b一定增大,c可能增大 B、b可能不变,c一定增大 C、b一定不变,c一定增大 D、b可能增大,c可能不变10. 如图,反比例函数 的图象经过正方形ABCD的顶点A和中心E,若点D的坐标为 ,则k的值为
斐波那契螺旋线
6. 已知一个多边形的内角和是540°,则这个多边形是( )A、四边形 B、五边形 C、六边形 D、七边形7. 若 ,其中a为整数,则a的值是( )A、1 B、2 C、3 D、48. 化简 的结果是( )A、a-b B、a+b C、 D、9. 随机调查某市100名普通职工的个人年收入(单位:元)情况,得到这100人年收入的数据,记这100个数据的平均数为a,中位数为b,方差为c.若将其中一名职工的个人年收入数据换成世界首富的年收入数据,则a一定增大,那么对b与c的判断正确的是( )A、b一定增大,c可能增大 B、b可能不变,c一定增大 C、b一定不变,c一定增大 D、b可能增大,c可能不变10. 如图,反比例函数 的图象经过正方形ABCD的顶点A和中心E,若点D的坐标为 ,则k的值为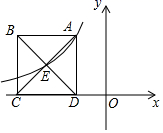 A、2 B、-2 C、 D、
A、2 B、-2 C、 D、二、填空题
-
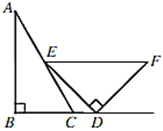
11. = .12. 分解因式:3x2-6x=.13. 已知点 的坐标是 ,则点 在第象限.14. 一副三角尺如图摆放,D是 延长线上一点,E是 上一点, , , ,若 ∥ ,则 等于度.
 15. 若关于 的一元一次不等式组 的解是 ,则 的取值范围是 .16. 在平行四边形ABCD中, , ,点E为BC中点,连结AE,将 沿AE折叠到△AB´E的位置,若 ,则点B´到直线BC的距离为.
15. 若关于 的一元一次不等式组 的解是 ,则 的取值范围是 .16. 在平行四边形ABCD中, , ,点E为BC中点,连结AE,将 沿AE折叠到△AB´E的位置,若 ,则点B´到直线BC的距离为.三、解答题
-
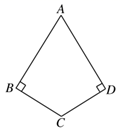
17. 先化简,再求值: ,其中 .18. 解方程: .19. 已知:如图, , , ,求证: .
 20. 如图,在平面直角坐标系 中,已知一次函数 的图象与反比例函数 的图象相交于A , B两点.且点A的坐标为 .
20. 如图,在平面直角坐标系 中,已知一次函数 的图象与反比例函数 的图象相交于A , B两点.且点A的坐标为 .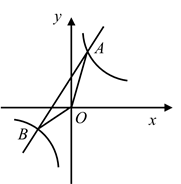 (1)、求该一次函数的解析式;(2)、求 的面积.21. 争创全国文明城市,从我做起.尚理中学在八年级开设了文明礼仪校本课程,为了解学生的学习情况,随机抽取了20名学生的测试成绩,分数如下:
(1)、求该一次函数的解析式;(2)、求 的面积.21. 争创全国文明城市,从我做起.尚理中学在八年级开设了文明礼仪校本课程,为了解学生的学习情况,随机抽取了20名学生的测试成绩,分数如下:94 83 90 86 94 88 96 100 89 82
94 82 84 89 88 93 98 94 93 92
整理上面的数据,得到频数分布表和扇形统计图:
等级
成绩/分
频数
A
a
B
8
C
5
D
4
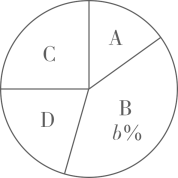
根据以上信息,解答下列问题.
(1)、填空: , ;(2)、若成绩不低于90分为优秀,估计该校1200名八年级学生中,达到优秀等级的人数;(3)、已知A等级中有2名女生,现从A等级中随机抽取2名同学,试用列表或画树状图的方法求出恰好抽到一男一女的概率.22. 某文具店最近有A,B两款毕业纪念册比较畅销,近两周的销售情况是:第一周A款销售数量是15本,B款销售数量是10本,销售总价是230元;第二周A款销售数量是20本,B款销售数量是10本,销售总价是280元.(1)、求A,B两款毕业纪念册的销售单价;(2)、若某班准备用不超过529元购买这两种款式的毕业纪念册共60本,求最多能够买多少本A款毕业纪念册.23. 如图, 内接于 , ,点E在直径CD的延长线上,且 .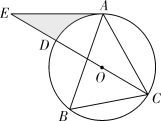 (1)、试判断AE与 的位置关系,并说明理由;(2)、若 ,求阴影部分的面积.24. 观察发现,如图1、图2,已知在 和 中, , ,将 固定, 绕点 旋转.
(1)、试判断AE与 的位置关系,并说明理由;(2)、若 ,求阴影部分的面积.24. 观察发现,如图1、图2,已知在 和 中, , ,将 固定, 绕点 旋转.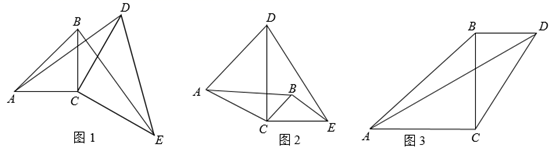 (1)、如图1,若 和 是等腰直角三角形, , , ,直接判断 与 之间的数量关系是;其中 的最大值为.(2)、如图2,若 和 是直角三角形, , ,判断 与 之间的数量关系,说明理由,并求出 的最大值.(3)、如图3,已知在 中, , ,以 为直角边向外作等腰 ,连接 ,求出 的最大值.25. 在平面直角坐标系 中,关于x的二次函数 的图象过点 , .
(1)、如图1,若 和 是等腰直角三角形, , , ,直接判断 与 之间的数量关系是;其中 的最大值为.(2)、如图2,若 和 是直角三角形, , ,判断 与 之间的数量关系,说明理由,并求出 的最大值.(3)、如图3,已知在 中, , ,以 为直角边向外作等腰 ,连接 ,求出 的最大值.25. 在平面直角坐标系 中,关于x的二次函数 的图象过点 , . (1)、求这个二次函数的表达式;(2)、求当 时,y的最大值与最小值的差;(3)、一次函数 的图象与二次函数 的图象交点的横坐标分别是a和b,且 ,求m的取值范围.
(1)、求这个二次函数的表达式;(2)、求当 时,y的最大值与最小值的差;(3)、一次函数 的图象与二次函数 的图象交点的横坐标分别是a和b,且 ,求m的取值范围.