人教A版必修2第八章立体几何单元测试卷

试卷更新日期：2021-05-10 类型：单元试卷

进入出卷网下载

一、单选题

1. 已知m，n为两条不同的直线， $α$ 和 $β$ 是两个不同的平面，下列为真命题的是（）

A、 $m ⊥ n ， m / / α \Rightarrow n ⊥ α$ B、 $n / / β ， β ⊥ α \Rightarrow n ⊥ α$ C、 $m / / n ， m ⊥ β \Rightarrow n ⊥ β$ D、 $m / / α ， n \subset α \Rightarrow m / / n$

查看试题解析
2. 已知某圆锥的轴截面是边长为4的正三角形，则它的体积为（）．

A、 $\frac{2 \sqrt{3}}{3} π$ B、 $\frac{4 \sqrt{3}}{3} π$ C、 $\frac{8 \sqrt{3}}{3} π$ D、 $2 \sqrt{3} π$

查看试题解析
3. 用到球心的距离为1的平面去截球，以所得截面为底面，球心为顶点的圆锥体积为 $\frac{8 π}{3}$ ，则球的表面积为（）

A、16π B、32π C、36π D、48π

查看试题解析
4. 某几何体由四棱锥和半个圆柱组合而成，其三视图如图所示，则该几何体的体积是（）

A、 $8 + π$ B、 $\frac{8}{3} + π$ C、 $8 + \frac{π}{3}$ D、 $\frac{8 + π}{3}$

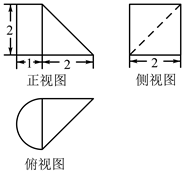查看试题解析
5. 蹴鞠（如图所示），2006年5月20日，已作为非物质文化遗产经国务院批准列入第一批国家非物质文化遗产名录．蹴有用脚蹴、踢、蹋的含义，鞠最早系外包皮革、内实米糠的球，因而蹴鞠就是指古人以脚蹴、蹋、踢皮球的活动，类似今日的足球．已知某鞠（球）的表面上有四个点 $A$ 、 $B$ 、 $C$ 、 $P$ ，且球心 $O$ 在 $P C$ 上， $A C = B C = 2$ ， $A C ⊥ B C$ ， $\tan ∠ P A B = \tan ∠ P B A = \frac{\sqrt{6}}{2}$ ，则该鞠（球）的表面积为（）．

A、5π B、 $7 \sqrt{2} π$ C、9π D、14π

查看试题解析
6. 如图， $A B C D - A_{1} B_{1} C_{1} D_{1}$ 为正方体，下面结论错误的是（）

A、 $B D / /$ 平面 $C B_{1} D_{1}$ B、 $A C_{1} ⊥ B D$ C、 $A C_{1} ⊥$ 平面 $C B_{1} D_{1}$ D、异面直线 $A D$ 与 ${CB}_{1}$ 角为 $60 °$

查看试题解析
7. 四棱锥 $S - A B C D$ 中，侧面 $S B C$ 为等边三角形，底面 $A B C D$ 为矩形， $B C = 2$ ， $A B = a$ ，点 $F$ 是棱 $A D$ 的中点，顶点 $S$ 在底面 $A B C D$ 的射影为 $H$ ，则下列结论正确的是（）

A、棱 $S C$ 上存在点 $P$ 使得 $P D //$ 面 $B S F$ B、当 $H$ 落在 $A D$ 上时， $a$ 的取值范围是 $(0 ， \sqrt{3}]$ C、当 $H$ 落在 $A D$ 上时，四棱锥 $S - A B C D$ 的体积最大值是2 D、存在 $a$ 的值使得点 $B$ 到面 $S F C$ 的距离为 $\sqrt{3}$

查看试题解析
8. 在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，点 $P$ 是线段 $B C_{1}$ 上的动点，以下结论：
① $A_{1} P //$ 平面 $A C D_{1}$ ；② $A_{1} P ⊥ B_{1} D$ ；③三棱锥 $P - A C D_{1}$ ，体积不变；④ $P$ 为 $B C_{1}$ 中点时，直线 $P C$ 与平面 $A C D_{1}$ 所成角最大.

其中正确的序号为（）

A、①④ B、②④ C、①②③ D、①②③④

查看试题解析

二、多选题

9. 若四面体各棱的长是1或2，且该四面体的棱长不全相等，则其体积的值可能为（）

A、 $\frac{\sqrt{11}}{6}$ B、 $\frac{\sqrt{14}}{12}$ C、 $\frac{\sqrt{11}}{12}$ D、 $\sqrt{2}$

查看试题解析
10. 如图，在边长为4的正方形 $A B C D$ 中，点 $E$ 、 $F$ 分别在边 $A B$ 、 $B C$ 上（不含端点）且 $B E = B F$ ，将 $△ A E D$ ， $△ D C F$ 分别沿 $D E$ ， $D F$ 折起，使 $A$ 、 $C$ 两点重合于点 $A_{1}$ ，则下列结论正确的有（）．

A、 $A_{1} D ⊥ E F$ B、当 $B E = B F = \frac{1}{2} B C$ 时，三棱锥 $A_{1} - D E F$ 的外接球体积为 $\sqrt{6} π$ C、当 $B E = B F = \frac{1}{4} B C$ 时，三棱锥 $A_{1} - D E F$ 的体积为 $\frac{2 \sqrt{17}}{3}$ D、当 $B E = B F = \frac{1}{4} B C$ 时，点 $A_{1}$ 到平面 $D E F$ 的距离为 $\frac{4 \sqrt{17}}{7}$

查看试题解析
11. 已知球O为正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的内切球，平面 $A_{1} C_{1} B$ 截球O的面积为 $24 π$ ，下列命题中正确的有（）

A、异面直线 $A C$ 与 $B C_{1}$ 所成的角为60° B、 $B D_{1} ⊥$ 平面 $A_{1} C_{1} B$ C、球O的表面积为 $36 π$ D、三棱锥 $B_{1} - A_{1} C_{1} B$ 的体积为288

查看试题解析
12. 如图，已知长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，四边形 $A B C D$ 为正方形， $A B = 2$ ， $A A_{1} = \sqrt{2}$ ， $E$ ， $F$ 分别为 $A B$ ， $B C$ 的中点.则（）

A、 $A_{1} E ⊥ D F$ B、点 $A_{1}$ ､ $E$ ､ $F$ ､ $C_{1}$ 四点共面 C、直线 $C_{1} D$ 与平面 $B B_{1} C_{1} C$ 所成角的正切值为 $\sqrt{2}$ D、三棱锥 $E - C_{1} D F$ 的体积为 $\frac{\sqrt{2}}{2}$

查看试题解析

三、填空题

13. 用总长 $11$ m的钢条制作一个长方体容器的框架，如果所制容器底面一条边比另一条边长1m，则该容器容积的最大值为m³（不计损耗）．

查看试题解析
14. 如图所示，在三棱锥 $B - A C D$ 中， $∠ A B C = ∠ A B D = ∠ D B C = \frac{π}{3}$ ， $A B = 3$ ， $B C = B D = 2$ ，则三棱锥 $B - A C D$ 的外接球的表面积为.

查看试题解析
15. 某三棱锥的三视图是三个边长相等的正方形及对角线，若该三棱锥的体积是 $\frac{8}{3}$ ，则它的表面积是，外接球的体积是．

查看试题解析
16. 已知正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的体积为8，点E，F分别是线段CD，BC的中点，平面 $α$ 过点 $A_{1}$ ，E，F且与正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 形成一个截面图形，现有如下说法：
①截面图形是一个六边形；

②若点I在正方形 $C D D_{1} C_{1}$ 内（含边界位置），且 $I \in$ 平面 $α$ ，则点I的轨迹长度为 $\frac{2 \sqrt{13}}{3}$ ；

③截面图形的周长为 $2 \sqrt{13} + \sqrt{2}$ ；

则说法正确命题的序号为．

查看试题解析

四、解答题

17. 如图， $△ A B C$ 中， $A C = B C = \frac{\sqrt{2}}{2} A B$ ， $A B E D$ 是边长为 $1$ 的正方形，平面 $A B E D$ ⊥平面 $A B C$ ，若 $G$ 、 $F$ 分别是 $E C$ 、 $B D$ 的中点．

(1)、求证： $G F //$ 平面 $A B C$ ；

(2)、求证： $A C$ ⊥平面 $E B C$ ．

查看试题解析
18. 如图，在三棱锥 $P - A B C$ 中， $PA ⊥ AB$ ， $PA ⊥ BC$ ， $AB ⊥ B C$ ， $PA = AB = BC = 2$ ， $D$ 为线段 $A C$ 的中点， $E$ 为线段 $P C$ 上一点．

(1)、求证：平面 $B D E ⊥$ 平面 $P A C$ ；

(2)、当 $P A / /$ 面 $B D E$ 时，求三棱锥 $E - B C D$ 的体积．

查看试题解析
19. 已知四棱锥 $P - A B C D$ 及其三视图如图所示，其底面 $A B C D$ 是正方形，且平面 $A B C D ⊥$ 平面 $P D C$ ，当 $M$ 、 $N$ 分别是棱 $P C$ 、 $A D$ 的中点时，连接 $M N$ 、 $B M$ ．

(1)、证明：直线 $M N //$ 平面 $P A B$ ；

(2)、求直线 $M B$ 与平面 $P A B$ 所成角的正弦值．

查看试题解析
20. 如图，三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A B ⊥$ 侧面 $B B_{1} C_{1} C$ ，已知 $∠ B C C_{1} = \frac{π}{3}$ ， $B C = 1$ ， $A B = C_{1} C = 2$ ，点E是棱 $C_{1} C$ 的中点.

(1)、求证： $B C ⊥$ 平面 $A B C_{1}$ ；

(2)、求二面角 $A - B_{1} E - A_{1}$ 的余弦值.

查看试题解析
21. 在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为菱形，平面 $P A D ⊥$ 平面 $A B C D$ ， $△ P A D$ 为等边三角形， $E$ 为 $P C$ 中点.

(1)、求证： $P A / /$ 平面 $B D E$ .

(2)、若 $P A = 4$ ，三棱锥 $C - E B D$ 的体积为 $4$ ，求二面角 $C - D E - B$ 的正弦值.

查看试题解析
22. 如图，在直角梯形 $A B C D$ 中， $A B // D C$ ， $∠ B A D = 90^{\circ}$ ， $A B = 4$ ， $A D = 2$ ， $D C = 3$ ，点 $E$ 在 $C D$ 上，且 $D E = 2$ ，将 $△ A D E$ 沿 $A E$ 折起，使得平面 $A D E ⊥$ 平面 $A B C E$ （如图）. $G$ 为 $A E$ 中点.

(1)、求证： $D G ⊥$ 平面 $A B C E$ ；

(2)、求四棱锥 $D - A B C E$ 的体积；

(3)、在线段 $B D$ 上是否存在点 $P$ ，使得 $C P / /$ 平面 $A D E$ ？若存在，求 $\frac{B P}{B D}$ 的值；若不存在，请说明理由.

查看试题解析

人教A版必修2第八章 立体几何单元测试卷

一、单选题

二、多选题

三、填空题

四、解答题

人教A版必修2第八章立体几何单元测试卷