浙教版备考2021年中考数学一轮复习专题40 定义新运算

试卷更新日期：2021-05-09 类型：一轮复习

进入出卷网下载

一、单选题

1. 对于实数 $a$ ， $b$ ，定义运算“ $Δ$ ”满足： $a Δ b = k_{1} a^{2} + k_{2} a b + k_{3} b^{2}$ ．若 $2 Δ (- 3) = (- 3) Δ 2$ ，则（）

A、 $k_{1} = k_{2}$ B、 $k_{1} = k_{3}$ C、 $k_{2} = k_{3}$ D、 $k_{1} + k_{3} = 2 k_{2}$

查看试题解析
2. 对于实数a、b，定义运算“★”：a★b= ${\begin{array}{l} a^{2} - b (a \leq b) \\ b^{2} - a (a > b) \end{array}$ ，关于x的方程（2x+1）★（2x-3）=t恰好有两个不相等的实数根，则t的取值范围是（）

A、t＜ $\frac{15}{4}$ B、t＞ $\frac{15}{4}$ C、t＜ $- \frac{17}{4}$ D、t＞ $- \frac{17}{4}$

查看试题解析
3. 定义一种运算“☆”，其规则为 $a ☆ b = \sqrt{a^{2} + b^{2}}$ ，如 $3 ☆ 4 = \sqrt{3^{2} + 4^{2}} = \sqrt{25} = 5$ ，根据这个规则计算 $5 ☆ 12$ 的值是（）

A、 $\sqrt{13}$ B、13 C、5 D、6

查看试题解析
4. 对于任意不相等的两个实数a，b，定义运算：a※b= $a^{2} - b^{2}$ +1例如3※2= $3^{2} - 2^{2} + 1$ =6，那么(-5)※4的值为（）

A、-40 B、-32 C、18 D、10

查看试题解析
5. 对于任意非零实数a， b，定义运算“※"如下： "a※b" = $\frac{a - b}{a b}$ ，则1※2+ 2※3+ 3※4+…+ 2019※2020的值为（）

A、 $- \frac{1}{2020}$ B、 $\frac{1}{2020}$ C、 $\frac{2019}{2020}$ D、 $- \frac{2019}{2020}$

查看试题解析
6. 对于二次函数y=ax²+bx+c(a≠0)，我们把使函数值等于0的实数x叫做这个函数的零点，则二次函数y=x²－mx－5(m为实数)的零点的个数是（）

A、1 B、2 C、0 D、不能确定

查看试题解析
7. 任何一个正整数n都可以进行这样的分解：n＝s×t（s，t是正整数，且s≤t），如果p×q在n的所有分解中两因数之差的绝对值最小，我们就称p×q是n的最优分解，并规定：F（n）＝ $\frac{p}{q}$ .例如24可以分解成1×24，2×12，3×8，4×6这四种，这时就有F（24）＝ $\frac{4}{6}$ ＝ $\frac{2}{3}$ .给出下列关于F（n）的说法：①F（6）＝ $\frac{2}{3}$ ；②F（16）＝1；③F（n²﹣n）＝1﹣ $\frac{1}{n}$ ；④若n是一个完全平方数，F（n）＝1.其中说法正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
8. 定义一种新运算 $\int_{b}^{a} n \cdot x^{n - 1} d x$ ＝aⁿ﹣bⁿ ，例如 $\int_{n}^{k} 2 x d x$ ＝k²﹣n² ，若 $\int_{m^{2} - 1}^{m - 1} - x^{- 2} d x$ ＝﹣ $\frac{1}{2}$ ，则m为（　　）

A、﹣1+ $\sqrt{2}$ B、﹣1﹣ $\sqrt{2}$ C、 $\sqrt{2}$ ±1 D、﹣1± $\sqrt{2}$

查看试题解析
9. 若点M，N分别是两条线段a和b上任意一点，则线段MN长度的最小值叫做线段a与线段b的“理想距离”。已知O（0，0），A（1，1），B（3，k），C（3，k+2），线段BC与线段OA的“理想距离”为2，则k的取值错误的是（）

A、-1 B、0 C、1 D、2

查看试题解析
10. 若“！”是一种数学运算符号，并且1！=1，2！=2×1，3！=3×2×1，且公式 $C_{n}^{m} = \frac{n (n-1) (n-2) ... (n - m + 1)}{m ！}$ ，则 $C_{12}^{5}$ + $C_{12}^{6}$ =（）

A、 $C_{12}^{11}$ B、 $C_{13}^{5}$ C、 $C_{13}^{6}$ D、 $C_{13}^{11}$

查看试题解析

二、填空题

11. 对于三个互不相等的有理数a ， b ， c ，我们规定符号 $\max {a ， b ， c}$ 表示a ， b ， c三个数中较大的数，例如 $\max {2 ， 3 ， 4} = 4$ .按照这个规定则方程 $\max {x ， - x ， 0} = 3 x - 2$ 的解为．

查看试题解析
12. 对于正整数a、b、c、d，符号 $| \begin{matrix} a & b \\ d & c \end{matrix} |$ 表示运算ac-bd，已知1< $| \begin{matrix} 1 & b \\ d & 4 \end{matrix} |$ <3，则b+d=.

查看试题解析
13. 若规定 $[a]$ 表示不超过 $a$ 的最大整数，例如 $[4.3] = 4$ ，若 $m = [π + 1]$ ， $n = [2.1]$ ，则在 $[m + \frac{9}{4} n]$ 此规定下的值为.

查看试题解析
14. 日常生活中主要运用“十进制”数，而“十六进制”广泛应用于电子技术、计算机编程等领域．十六进制在数学中是一种“逢16进1”的进位制，一般用数字0到9和字母A到F表示，其中用A，B，C，D，E，F分别表示10，11，12，13，14，15．如(2AF5)₁₆表示十六进制数，将它转换成十进制形式是2×16³+10×16²+15×16¹+5×16⁰=10997，那么将十进制数2020转换成十六进制数表示为．

查看试题解析
15. 定义[a ， b ， c]为函数y＝ax²+bx+c的特征数，下面给出特征数为[2m ， 1﹣m ， ﹣1﹣m]的函数的一些结论：
①当m＝﹣1时，函数图象的顶点坐标是（ $\frac{1}{2}$ ， $\frac{1}{2}$ ）；

②当m＞0时，函数图象截x轴所得的线段长度大于 $\frac{3}{2}$ ；

③当m＜0时，函数在 $x > \frac{1}{4}$ 时，y随x的增大而减小；

④当m≠0时，函数图象经过x轴上一个定点．

其中正确的结论有．（只需填写序号）

查看试题解析
16. 对于实数a，b定义运算“*”：a*b=a²-ab(a≤b)，a*b=b²-ab(a>b)，关于x的方程(2x-1) * (x-1) =m恰有三个不相等的实数根，则m的取值范围

查看试题解析

三、综合题

17. 对于有理数 $x ， y$ ，定义一种新的运算“*”： $x * y = a x + b y + c$ ，其中 $a ， b ， c$ 为常数，等式右边是通常的加法与乘法运算，已知 $3 * 5$ ＝15， $4 * 7$ ＝28，求 $1 * 1$ 的值

查看试题解析
18. 用[x]表示不大于x的最大整数，如[2.1]=2，[-4.5]=-5，已知x₁ ，x₂是方程6x+7=3[x]的解，且x₁<x₂ ，点A(x₁ ， y₁)和B (x₂ ， y₂)是直线y=-2x-1上的两点，试比较y₁与y₂+l的大小。

查看试题解析
19. 如图所示，现有3×3的数阵A，数阵每个位置所对应的数都是1，2或3.定义a*b为数阵中第a行第b列的数.例如：数阵A第3行第2列所对应的数是3，所以3*2=3.

(1)、对于数阵A，2*3的值为；若2*3=2*x，则x的值为.

(2)、若一个3×3的数阵对任意的a，b，c均满足以下条件：
条件一：a*a=a.条件二：（a*b）*c=a*c.

则称此数阵是“有趣的”.

①请判断数阵A是否是“有趣的”.你的结论：（填“是”或“否”）.

②已知一个“有趣的”数阵满足1*2=2，试计算2*1的值.

③是否存在“有趣的”数阵，对任意的a，b满足交换律a*b=b*a?若存在，请写出一个满足条件的数阵；若不存在，请说明理由.

查看试题解析
20. 定义：在平面直角坐标系中，对于任意两点A（a，b），B(c，d)，若点T（x，y)满足x= $\frac{a + c}{3}$ ，y= $\frac{b + d}{3}$ ，那么称点T是点A，B的融合点。
例如：A（-1，8），B（4，-2），当点T（x，y）满是x= $\frac{- 1 + 4}{3}$ =1，y= $\frac{8 + (- 2)}{3}$ =2时，则点T（1，2）是点A，B的融合点，

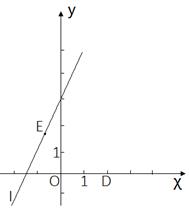(1)、已知点A（-1，5），B(7，7)，C（2，4），请说明其中一个点是另外两个点的融合点。

(2)、如图，点D（3，0），点E（t，2t+3）是直线l上任意一点，点T（x，y)是点D，E的融合点。
①试确定y与x的关系式。

②若直线ET交x轴于点H，当△DTH为直角三角形时，求点E的坐标。

查看试题解析
21. 给出如下规定：若实数 $a$ 与 $b$ 的差等于这两个数的积，则称实数对 $(a ， b)$ 为“关联数”.如实数对 $(- 2 ， 2)$ ，因为 $- 2 - 2 = - 4$ ， $(- 2) \times 2 = - 4$ ，所以实数对 $(- 2 ， 2)$ 是关联数；又如实数对 $(0 ， 0)$ 是关联数.

(1)、若实数对 $(a ， b)$ 为“关联数”，则 $a$ ， $b$ 应满足的条件用含 $a$ ， $b$ 的等式表示为.

(2)、判断下列实数对是否是关联数？
① $(1 ， - \frac{1}{2})$ ；

② $(- \frac{3}{4} ， - 3)$ .

(3)、若实数对 $(\frac{2 x - 1}{2} ， - 5)$ 是关联数，求 $x$ 的值.

(4)、是否存在非零实数 $m$ ， $n$ ，使实数对 $(2 m ， 3 n)$ 与 $(3 m ， 2 n)$ 都是关联数？若存在，求出 $m$ ， $n$ 的值；若不存在，请说明理由.

查看试题解析
22. 定义：在平面直角坐标系中，对于任意两点A(a，b)，B(c，d)，若点T(x，y)满足x= $\frac{a + c}{3}$ ，y= $\frac{b + d}{3}$ 那么称点T是点A，B的融合点。
例如：A(-1，8)，B(4，-2)，当点T(x，y)满足x= $\frac{- 1 + 4}{3}$ =1，y= $\frac{8 + (- 2)}{3}$ =2时，则点T(1，2)是点A，B的融合点。

(1)、已知点A(-1，5)，B(7，7)，C(2，4)，请说明其中一个点是另外两个点的融合点。

(2)、如图，点D(3，0)，点E(t，2+3)是直线l上任意一点，点T(x，y)是点D，E的融合点。
①试确定y与x的关系式。

②若直线ET交x轴于点H，当△DTH为直角三角形时，求点E的坐标。

查看试题解析
23. 在直角坐标系xOy中，对于点P(x，y) 和Q(x， y′) .给出如下定义：若 $y^{'} = {\begin{matrix} y (x \geq 0) \\ - y (x < 0) \end{matrix}$ ，则称点Q 为点P 的“可控变点” . 例如：点（1，2）的可控变点为点（1，2），点（-1，3）的可控变点为点（-1，-3）.

(1)、点（-6，-3）的可控变点坐标为．

(2)、若点P在函数y＝－x² ＋16的图象上，其可控变点Q的纵坐标y′是7，求可控变点Q的横坐标．

查看试题解析
24. 如果关于x的一元二次方程ax²+bx+c=0有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”，研究发现了此类方程的一般性结论：设其中一根为t，则另一个根为2t，因此ax²+bx+c=a(x−t)(x−2t)=ax²−3atx+2t²a，可得；即当时，方程ax²+bx+c=0为倍根方程；下面我们根据此结论来解决问题：

(1)、方程①x²−x−2=0；方程②x²−6x+8=0这两个方程中，是倍根方程的是(填序号即可)；

(2)、若(x−2)(mx+n)=0是倍根方程，求4m²+5mn+n²的值；

(3)、关于x的一元二次方程 $x^{2} - \sqrt{m} x + \frac{2}{3} n = 0$ (m⩾0)是倍根方程，且点A(m，n)在一次函数y=3x−8的图象上，求此倍根方程的表达式

查看试题解析
25. 根据同底数幂的乘法法则，我们发现： $a^{m + n} = a^{m} \cdot a^{n}$ （其中 $a \neq 0$ ， $m$ ， $n$ 为正整数），类似地我们规定关于任意正整数 $m$ ， $n$ 的一种新运算： $h (m + n) = h (m) \cdot h (n)$ ，请根据这种新运算解决以下问题：

(1)、若 $h (1) = - 1$ ，则 $h (2) =$ ； $h (2019) =$ ；

(2)、若 $h (7) = 128$ ，求 $h (2)$ ， $h (8)$ 的值；

(3)、若 $\frac{h (4)}{h (2)} = 4$ ，求 $h (2)$ 的值；

(4)、若 $\frac{h (4)}{h (2)} = 4$ ，直接写出 $\frac{h (2)}{h (1)} + \frac{h (4)}{h (2)} + \frac{h (6)}{h (3)} + \dots + \frac{h (2 n)}{h (n)}$ 的值.

查看试题解析
26. 对实数a，b定义运算 $a * b = {\begin{cases} a^{2} + b ， (a \geq b) \\ \frac{2}{a} ， (a < b) \end{cases}$

(1)、求函数 $y = x * (2 x - 1)$ 的解析式；

(2)、若点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ ( $x_{1} < x_{2}$ )在函数 $y = x * (2 x - 1)$ 的图像上，且A，B两点关于坐标原点成中心对称，求点A的坐标；

(3)、关于的方程 $x * (2 x - 1) = m$ 恰有三个互不相等的实数根，则m的取值范围是

查看试题解析