浙教版备考2021年中考数学一轮复习专题39 探索数与图的规律

试卷更新日期：2021-05-09 类型：一轮复习

进入出卷网下载

一、单选题

1. QQ空间是一个展示自我和沟通交流的网络平台.它既是网络日记本，又可以上传图片、视频等.QQ空间等级是用户资料和身份的象征，按照空间积分划分不同的等级.当用户在10级以上，每个等级与对应的积分有一定的关系.现在知道第10级的积分是90，第11级的积分是160，第12级的积分是250，第13级的积分是360，第14级的积分是490……若某用户的空间积分达到1000，则他的等级是（）

A、15 B、16 C、17 D、18

查看试题解析
2. 小王利用计算机设计了一个计算程序，输人和输出的数据如下表所示，当输人数据为8时，输出的数据为（）

输入 … 1 2 3 4 5 …

输出 … $\frac{1}{2}$ $\frac{2}{5}$ $\frac{3}{10}$ $\frac{4}{17}$ $\frac{5}{26}$ …

A、 $\frac{8}{61}$ B、 $\frac{1}{62}$ C、 $\frac{8}{63}$ D、 $\frac{8}{65}$

查看试题解析
3. 计算： $3^{1} - 1 = 2$ ， $3^{2} - 1 = 8$ ， $3^{3} - 1 = 26$ ， $3^{4} - 1 = 80$ ， $3^{5} - 1 = 242$ ，……，归纳各计算结果中的个位数字的规律，猜测 $3^{2021}$ 的个位数字是（）

A、0 B、1 C、2 D、3

查看试题解析
4. 让我们来做一个数字游戏，第一步取一个自然数 $n_{1} = 5$ ，计算 $n_{1}^{2} + 1$ 得 $a_{1}$ ；第二步，算出 $a_{1}$ 的各位数字之和得 $n_{2}$ ，计算 $n_{2}^{2} + 1$ 得 $a_{2}$ ；第三步，算出 $a_{2}$ 的各位数字之和得 $n_{3}$ ，计算 $n_{3}^{2} + 1$ ；……依次类推，则 $a_{2011}$ 为（）

A、26 B、65 C、122 D、5

查看试题解析
5. 下列图形都是由面积为1的正方形按一定的规律组成的，其中，第1个图形中面积为1的正方形有9个，第2个图形中面积为1的正方形有14个，……，按此规律，则第几个图形中面积为1的正方形的个数为2019个（）

A、402 B、403 C、404 D、405

查看试题解析
6. 如图，已知正方形 $A_{1} A_{2} A_{3} A_{4}$ 的边长为1，延长 $A_{1} A_{2}$ 到 $B_{1}$ ，使得 $B_{1} A_{2} = A_{1} A_{2}$ ，延长 $A_{2} A_{3}$ 到 $B_{2}$ ，使得 $B_{2} A_{3} = A_{2} A_{3}$ ，以同样的方式得到 $B_{3} ， B_{4}$ ，连接 $B_{1} ， B_{2} ， B_{3} ， B_{4}$ ，得到第2个正方形 $B_{1} B_{2} B_{3} B_{4}$ ，再以同样方式得到第3个正方形 $C_{1} C_{2} C_{3} C_{4}$ ，……，则第2020个正方形的边长为（）

A、2020 B、 ${(\sqrt{5})}^{2019}$ C、 ${(\sqrt{5})}^{2020}$ D、 $5^{2020}$

查看试题解析
7. 如图，圆上有五个点，这五个点将圆分成五等份（每一份称为一段弧长），把这五个点按顺时针方向依次编号为1，2，3，4，5，若从某一点开始，沿圆周顺时针方向行走，点的编号是数字几，就走几段弧长，我们把这种走法称为一次“移位”.如：小明在编号为3的点，那么他应走3段弧长，即从3→4→5→1为第1次“移位”，这时他到达编号为1的点，那么他应走1段弧长，即从1→2为第2次“移位”.若小明从编号为4的点开始，经过2020次“移位”后，他到达编号为（）

A、1 B、2 C、4 D、5

查看试题解析
8. 对点(x，y)的一次操作变换记为P₁(x，y)，定义其变换法则如下：P₁(x，y)＝(x＋y，x－y)；且规定P_n(x，y)＝P₁(P_n_－1(x，y))(n为大于1的整数).如P₁(1，2)＝(3，－1)，P₂(1，2)＝P₁(P₁(1，2))＝P₁(3，－1)＝(2，4)，P₃(1，2)＝P₁(P₂(1，2))＝P₁(2，4)＝(6，－2).则P_{2 021}(1，－1)＝：（）

A、(0，2^{1 010}) B、(0，－2^{1 010}) C、(0，－2^{1 011}) D、(0，2^{1 011})

查看试题解析
9. 如图，用火柴棍分别搭一排三角形组成的图形和一排正方形组成的图形，三角形、正方形的每一边用一根火柴棒.如果搭这两个图案一共用了2030根火柴棒，且正方形的个数比三角形的个数的少4个，则搭成的三角形的个数是（）

A、429 B、409 C、408 D、404

查看试题解析
10. 将连续正整数按如图所示的位置顺序排列：根据排列规律，则2021应在（）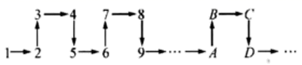

A、A处 B、B处 C、C处 D、D处

查看试题解析

二、填空题

11. 从1开始，将连续的奇数相加，和的情况有如下规律：1=1=1²；1+3=4=2²；1+3+5=9=3²；1+3+5+7=16=4²；1+3+5+7+9=25=5²；…按此规律请你猜想从1开始，将前1000个奇数（即当最后一个奇数是1999时），它们的和是。（结果用科学记数法表示）

查看试题解析
12. 如图是某广场用地板铺设的部分图案，中央是一块正六边形的地板砖，周围是正三角形和正方形的地板砖.从里向外的第1层包括6个正方形和6个正三角形，第2层包括6个正方形和18个正三角形，依此递推，第10层中含有正三角形个数为个.

查看试题解析
13. 如图所示，每个图案都由若干个棋子摆成，按照此规律摆下去，第n个图案中棋子的总个数可用含n的代数式表示为.

查看试题解析
14. 我国古代数学家刘徽创造的“割圆术”，利用了圆内接正多边形和外切正多边形的面积或周长，无限逼近圆来近似估计圆的面积或周长，从而估算出π的范围.如图1，用圆内接正方形和外切正方形周长可得2 $\sqrt{2}$ <r<4，那么利用图2中的圆内接正六边形和外切正六边形周长可进一步将π的范围缩小到(结果保留根号)

查看试题解析
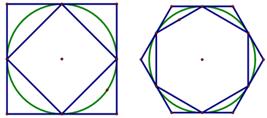15. 如图，在平面直角坐标系中，等边△A₁B₁C₁ ，等边△A₂B₂C₂ ，等边△A₃B₃C₃ ， …中A₁B₁ ， A₂B₂ ， A₃B₃ ， …平行于x轴，点C₁ ， C₂ ， C₃ ， …在y轴正半轴上，三边垂直平分线的交点在原点，A₁B₁ ， A₂B₂ ， A₃B₃ ， …的长依次为 $\sqrt{3}$ ， $2 \sqrt{3}$ ， $3 \sqrt{3}$ ，….以此类推，则等边△A₂₀₂₀B₂₀₂₀C₂₀₂₀的顶点A₂₀₂₀的坐标为.

查看试题解析
16. 有一列按规律排列的代数式：b，2b﹣a，3b﹣2a，4b﹣3a，5b﹣4a，…，相邻两个代数式的差都是同一个整式，若第4个代数式的值为8，则前7个代数式的和的值为.

查看试题解析
17. 将数1个1，2个 $\frac{1}{2}$ ，3个 $\frac{1}{3}$ ，…，n个 $\frac{1}{n}$ （n为正整数）顺次排成一列：1， $\frac{1}{2}$ ， $\frac{1}{2}$ ， $\frac{1}{3}$ ， $\frac{1}{3}$ ， $\frac{1}{3}$ ，…， $\frac{1}{n}$ ， $\frac{1}{n}$ ，记a₁=1，a₂= $\frac{1}{2}$ ，a₃= $\frac{1}{2}$ ，…，S₁=a₁ ， S₂=a₁+a₂ ， S₃=a₁+a₂+a₃ ， …，S_n=a₁+a₂+…+a_n ，则S₂₀₁₉=.

查看试题解析
18. 观察图形：图中是边长为1，2，3 …的正方形：当边长 $n$ ＝1时，正方形被分成2个大小相等的小等腰直角三角形；当边长 $n$ ＝2时，正方形被分成8个大小相等的小等腰直角三角形；当边长 $n$ ＝3时，正方形被分成18个大小相等的小等腰直角三角形；以此类推：当边长为 $n$ 时，正方形被分成大小相等的小等腰直角三角形的个数是。

查看试题解析

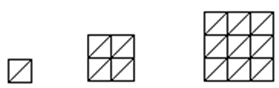
三、解答题

19. 对于正数x，规定 $f (x) = \frac{x}{1 + x}$ ，例如 $f (3) = \frac{3}{1 + 3} = \frac{3}{4}$ ， $f (\frac{1}{3}) = \frac{\frac{1}{3}}{1 + \frac{1}{3}} = \frac{1}{4} .$ 计算下列式子的值： $f (\frac{1}{2018}) + f (\frac{1}{2017}) + f (\frac{1}{2016}) + \dots + f (\frac{1}{3}) + f (\frac{1}{2}) + f (1) + f (1) + f (2) + f (3) + \dots + f (2016) + f (2017) + f (2018)$

查看试题解析
20. 一动点 $P$ 从数轴上的原点出发，沿数轴的正方向以每前进 $5$ 个单位、后退 $3$ 个单位的程序运动，已知点 $P$ 每秒前进或后退 $1$ 个单位，设 $x_{n}$ 表示第 $n$ 秒点 $P$ 在数轴上的位置所对应的数（如 $x_{4} = 4$ ， $x_{5} = 5$ ， $x_{6} = 4$ ），求 $x_{2011}$ 所对应的数.

查看试题解析
21. 阅读下列一段话，并解决后面的问题
观察下面一列数：1，2，4，8， $\dots ，$ 我们发现，这一列数从第2项起，每一项与它前一项的比都等于2.一般地，如果一列数从第二项起，每一项与它前一项的比都等于同一个常数，这一列数就叫做等比数列，这个常数叫做等比数列的公比.

(1)、、等比数列5，-15，45， $\dots ，$ 的第4项是.

(2)、如果一列数 $a_{1} ， a_{2} ， a_{3} ， a_{4} ， \dots$ 是等比数列，且公比为 $q$ ，那么根据上述的规定，有 $\frac{a_{2}}{a_{1}} = q$ ， $\frac{a_{3}}{a_{2}} = q$ ， $\frac{a_{4}}{a_{3}} = q \dots$ ，所以 $a_{2} = a_{1} q$ ， $a_{3} = a_{2} q = a_{1} q^{2}$ ， $a_{4} = a_{3} q = a_{1} q^{3} \dots$ ， $a_{n} =$ （用q和a₁的代数式表示）.

(3)、一个等比数列的第2项是10，第3项是20，求它的第1项与第4项.

查看试题解析
22. 为了给同学们创造更好的读书条件，学校准备新建一个长度为L的读书长廊，并准备用若干块带有花纹和没有花纹的两种规格、大小相同的正方形地面砖搭配在一起，按如图所示的规律拼成图案铺满长廊，已知每个小正方形地面砖的边长均为0.6m.

(1)、按图示规律，第一个图案的长度L₁=m，第二个图案的长度L₂=m.

(2)、请用代数式表示带有花纹的地面砖块数n与长廊的长度L_n之间的关系.

(3)、当长廊的长度L为36.6m时，请计算出所需带有花纹图案的瓷砖的块数.

查看试题解析
23. 用同样规格的黑白两种颜色的正方形，按如图的方式拼图，请根据图中的信息完成下列的问题．

(1)、在图②中用了块黑色正方形，在图③中用了块黑色正方形；

(2)、按如图的规律继续铺下去，那么第 $n$ 个图形要用块黑色正方形；

(3)、如果有足够多的白色正方形，能不能恰好用完90块黑色正方形，拼出具有以上规律的图形？如果可以请说明它是第几个图形；如果不能，说明你的理由．

查看试题解析
24. 我国在数的发展上有辉煌的成就，中国古代的算筹计数法可追溯到公元前五世纪，算筹是竹制的小棍，摆法有纵式和横式两种（如图1）.以算筹计数的方法是：摆个位为纵，十位为横，百位为纵，千位为横……，这样纵横依次交替，零以空格表示.如3257表示成“ ”.

①请用算筹表示数23，701；（分别表示在答题卷的图2、图3中）

②用三根算筹表示两位数（十位不能为零，且用完三根算筹），在答题卷的图4中摆出来，并在下方横线上填上所表示的数.（注：图4中的双方框个数过多）.

查看试题解析
25. 操作与推理：我们知道，任何一个有理数都可以用数轴上一个点来表示，根据下列题意解决问题：

(1)、已知x=2，请画出数轴表示出x的点：

(2)、在数轴上，我们把表示数2的点定为基准点，记作点O，对于两个不同的点A和B，若点A、 B到点O的距离相等，则称点A与点B互为基准等距变换点.例如图2，点A表示数-1，点B表示数5，它们与基准点O的距离都是3个单位长度，我们称点A与点B互为基准等距变换点.
①记已知点M表示数m，点N表示数n，点M与点N互为基准等距变换点.I.若m=3，则n=▲ ；II.用含m的代数式表示n=▲ ；

②对点M进行如下操作：先把点M表示的数乘以23，再把所得数表示的点沿着数轴向右移动2个单位长度得到点N，若点M与点N互为基准等距变换点，求点M表示的数；

③点P在点Q的左边，点P与点Q之间的距离为8个单位长度，对Q点做如下操作： Q₁为Q的基准等距变换点，将数轴沿原点对折后Q₁的落点为Q₂这样为一次变换： Q₃为Q₂的基准等距变换点，将数轴沿原点对折后Q₃的落点为Q₄这样为二次变换： Q₅为Q₄的基准等距变换点......，依此顺序不断地重复变换，得到Q₅ ， Q₆ ， Q₇....Q_n ，若P与Q_n.两点间的距离是4，直接写出n的值.

查看试题解析
26. 如图，一个电子跳蚤从数轴上的表示数a的点出发，我们把“向右运动两个单位或向左运动一个单位”作为一次操作。如：当a=3时，则一次操作后跳蚤可能的位置有两个，所表示的数分别是2和5。

(1)、若a=0，则两次操作后跳蚤所在的位置表示的数可能是多少？

(2)、若a=3，且跳蚤向右运动了20次，向左运动了n次。
①它最后的位置所表示的数是多少？ (用含 n的代数式表示)

②若它最后的位置所表示的数为10，求n的值。

(3)、若a=-10，跳蚤共进行了若干次操作，其中有50次是向左运动，且最后的位置所表示的数为260，求操作的次数。

查看试题解析

输入	…	1	2	3	4	5	…
输出	…	$\frac{1}{2}$	$\frac{2}{5}$	$\frac{3}{10}$	$\frac{4}{17}$	$\frac{5}{26}$	…