浙教版备考2021年中考数学一轮复习专题38 作图
试卷更新日期:2021-05-09 类型:一轮复习
一、单选题
-
1. 如图,已知三点A,B,C画直线AB,画射线AC,连接BC,按照上述语句画图正确的是( )A、
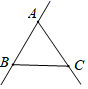 B、
B、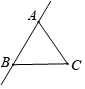 C、
C、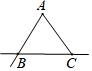 D、
D、 2. 如图,已知线段a、b( ),画一条线段AD,使它等于 ,正确的画法是( )
2. 如图,已知线段a、b( ),画一条线段AD,使它等于 ,正确的画法是( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 下列四种基本尺规作图分别表示,则对应选项中作法错误的是( )A、
3. 下列四种基本尺规作图分别表示,则对应选项中作法错误的是( )A、 作一个角等于已知角
B、
作一个角等于已知角
B、 作一个角的平分线
C、
作一个角的平分线
C、 作一条线段的垂直平分线
D、
作一条线段的垂直平分线
D、 过直线外一点P作已知直线的垂线
4. 下面是四位同学所作的 关于直线 对称的图形,其中正确的是( )A、
过直线外一点P作已知直线的垂线
4. 下面是四位同学所作的 关于直线 对称的图形,其中正确的是( )A、 B、
B、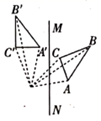 C、
C、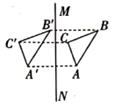 D、
D、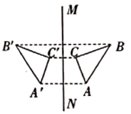 5. 图是世界休闲博览会吉祥物“晶晶”.右边的“晶晶”可由左边的“晶晶”经下列哪个变换得到( )
5. 图是世界休闲博览会吉祥物“晶晶”.右边的“晶晶”可由左边的“晶晶”经下列哪个变换得到( ) A、轴对称 B、平移 C、旋转 D、相似6. 如图,已知△ABC(AC<BC),用尺规在BC上确定一点P,使PA+PB=BC,则下列四种不同方法的作图中,作法正确的是( )
A、轴对称 B、平移 C、旋转 D、相似6. 如图,已知△ABC(AC<BC),用尺规在BC上确定一点P,使PA+PB=BC,则下列四种不同方法的作图中,作法正确的是( ) A、
A、 B、
B、 C、
C、 D、
D、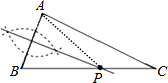 7. 如图,用尺规作出∠OBF=∠AOB,所画痕迹是( )
7. 如图,用尺规作出∠OBF=∠AOB,所画痕迹是( )
 A、以点B为圆心,OD为半径的弧 B、以点C为圆心,DC为半径的弧 C、以点E为圆心,OD为半径的弧 D、以点E为圆心,DC为半径的弧8. 如图,在△ 中, , 为钝角.按下列步骤作图:①以点B为圆心,适当长为半径作圆弧,交BC于点D,交AB于点E;②以点 为圆心, 长为半径作圆弧,交 于点 ;③以点 为圆心, 长为半径作圆弧,交②中所作的圆弧于点 ;④作射线 交 于点 .下列说法错误的是( )
A、以点B为圆心,OD为半径的弧 B、以点C为圆心,DC为半径的弧 C、以点E为圆心,OD为半径的弧 D、以点E为圆心,DC为半径的弧8. 如图,在△ 中, , 为钝角.按下列步骤作图:①以点B为圆心,适当长为半径作圆弧,交BC于点D,交AB于点E;②以点 为圆心, 长为半径作圆弧,交 于点 ;③以点 为圆心, 长为半径作圆弧,交②中所作的圆弧于点 ;④作射线 交 于点 .下列说法错误的是( ) A、 = B、 =∠ACB C、∠CHB=∠A+∠B D、 =∠HCB9. 如图,用直尺和圆规作一个角等于已知角,能得出 的依据是( )
A、 = B、 =∠ACB C、∠CHB=∠A+∠B D、 =∠HCB9. 如图,用直尺和圆规作一个角等于已知角,能得出 的依据是( ) A、 B、 C、 D、10. 过直线l外一点P作直线l的平行线,下列尺规作图中错误的是( )A、
A、 B、 C、 D、10. 过直线l外一点P作直线l的平行线,下列尺规作图中错误的是( )A、 B、
B、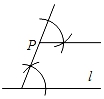 C、
C、 D、
D、 11. 下面三个基本作图的作图痕迹.关于三条弧①,②,③,有以下三种说法,
11. 下面三个基本作图的作图痕迹.关于三条弧①,②,③,有以下三种说法,
⑴弧①是以点O为圆心,以任意长为半径所作的弧;(2)弧②是以点A为圆心,以任意长为半径所作的弧;(3)弧③是以点O为圆心,以大于 DE的长为半径所作的弧.
其中正确说法的个数为( )
A、3个 B、2个 C、1个 D、0个12. 如图,在钝角△ABC中,过钝角顶点B作BD⊥BC交AC于点D.用尺规作图法在BC边上找一点P,使得点P到AC的距离等于BP的长,下列作法正确的是( ) A、作∠BAC的角平分线与BC的交点 B、作∠BDC的角平分线与BC的交点 C、作线段BC的垂直平分线与BC的交点 D、作线段CD的垂直平分线与BC的交点
A、作∠BAC的角平分线与BC的交点 B、作∠BDC的角平分线与BC的交点 C、作线段BC的垂直平分线与BC的交点 D、作线段CD的垂直平分线与BC的交点二、填空题
-
13. 作图:已知线段a、b,请用尺规作线段EF使EF=a+b.请将下列作图步骤按正确的顺序排列出来(只填序号).
作法:①以M为端点在射线MG上用圆规截取MF=b;②作射线EG;③以E为端点在射线EG上用圆规截取EM=a;④EF即为所求的线段。
14. 已知: ,求作 的外接圆,作法:①分别作线段BC,AC的垂直平分线EF和MN,它们交于点O;②以点O为圆心,OB的长为半径画弧,如图⊙O即为所求,以上作图用到的数学依据是.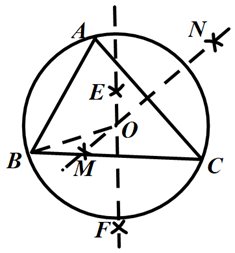 15. 如图,请说出甲树是怎样由乙树变换得到的: .
15. 如图,请说出甲树是怎样由乙树变换得到的: . 16. 如图,△ABC与△DEF是位似图形,点B的坐标为(3,0),则其位似中心的坐标为 .
16. 如图,△ABC与△DEF是位似图形,点B的坐标为(3,0),则其位似中心的坐标为 .
三、作图题
-
17. 有若干个完全相同的小正方体堆成的一个几何体,如图所示.请在方格纸上画出它的三视图.

 18. 画图题(1)、如图,已知三点A、B、C.
18. 画图题(1)、如图,已知三点A、B、C.
①画直线 ;
②射线 ;
③线段 ;
④在线段 上取点D;
⑤延长 到E,使 .
(2)、将下列各数在数轴上表示出来,并把它们用“>”连接起来.,2,3, .
19. 如图,已知△ABC,AC>AB,∠C=45°.请用尺规作图法,在AC边上求作一点P,使∠PBC=45°.(保留作图痕迹.不写作法) 20. 如图, 是 内一点,点 在AB上,按要求完成下列问题:
20. 如图, 是 内一点,点 在AB上,按要求完成下列问题: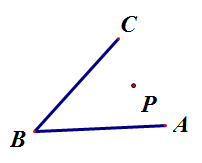
( 1 )过点 作 的垂线,垂足为点D;
( 2 )过点 作 的平行线,交AB于点E;
( 3 )比较线段 和 的大小,并说明理由.
21. 如图,在7×7的正方形网格中,每个小正方形的边长均为1,线段AB的端点均在小正方形的格点上(小正方形的顶点称为格点). (1)、在图中画一个Rt△ABC,使其同时满足以下三个条件:
(1)、在图中画一个Rt△ABC,使其同时满足以下三个条件:①A为直角顶点;②点C在格点上;③ ;
(2)、在(1)的条件下,请在网格中找到另一个格点D,满足tan∠CBD=1,连结CD,求线段CD的长.
22. 如图, 中, , , . (1)、用直尺和圆规作 的垂直平分线;(保留作图痕迹,不要求写作法)(2)、若(1)中所作的垂直平分线交 于点 ,求 的长.23. 如图,在 的网格中, 的三个顶点都在格点上.
(1)、用直尺和圆规作 的垂直平分线;(保留作图痕迹,不要求写作法)(2)、若(1)中所作的垂直平分线交 于点 ,求 的长.23. 如图,在 的网格中, 的三个顶点都在格点上. (1)、在图1中画出一个以 为边的▱ABDE,使顶点 , 在格点上.(2)、在图2中画出一条恰好平分 周长的直线 (至少经过两个格点).24. 请仅用无刻度的直尺画图,不写作法,保留画图痕迹.
(1)、在图1中画出一个以 为边的▱ABDE,使顶点 , 在格点上.(2)、在图2中画出一条恰好平分 周长的直线 (至少经过两个格点).24. 请仅用无刻度的直尺画图,不写作法,保留画图痕迹.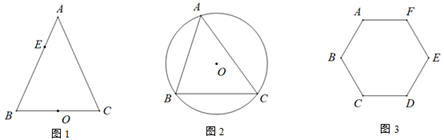
( 1 )如图1,点O是等腰△ABC底边BC的中点,E是AB上一点,请在AC上作出点F,使EF∥BC;
( 2 )如图2,△ABC为⊙O的内接三角形,请在AB,AC上分别作出点M,N,使MN∥BC;
( 3 )如图3,六边形ABCDE为正六边形,在AF上取一点H,使 .
25. 在建立平面直角坐标系的方格纸中,每个小方格都是边长为1的小正方形, 的顶点均在格点上,点P的坐标为 ,请按要求画图与作答 (1)、把 绕点P旋转180°得 .(2)、把 向右平移6个单位得 .(3)、 与 是否成中心对称,若是,找出对称中心 ,并写出其坐标.26. 黄金分割为“最美丽”的几何比率,广泛应用于图案设计。下图是一个包装盒的俯视图,线段AB是这个俯视图的中轴线,某公司想在中轴线AB上找到黄金分割点,安装视频播放器。
(1)、把 绕点P旋转180°得 .(2)、把 向右平移6个单位得 .(3)、 与 是否成中心对称,若是,找出对称中心 ,并写出其坐标.26. 黄金分割为“最美丽”的几何比率,广泛应用于图案设计。下图是一个包装盒的俯视图,线段AB是这个俯视图的中轴线,某公司想在中轴线AB上找到黄金分割点,安装视频播放器。 (1)、请你用尺规作图的方式找出这个点(作出一点即可,保留作图痕迹);(2)、证明你找到的点是线段AB的黄金分割点。27. 如图,楼房和旗杆在路灯下的影子如图所示.试确定路灯灯泡的位置,再作出小树在路灯下的影子.(不写作法,保留作图痕迹)
(1)、请你用尺规作图的方式找出这个点(作出一点即可,保留作图痕迹);(2)、证明你找到的点是线段AB的黄金分割点。27. 如图,楼房和旗杆在路灯下的影子如图所示.试确定路灯灯泡的位置,再作出小树在路灯下的影子.(不写作法,保留作图痕迹) 28. 已知:线段m,n求作:线段AB,使 .
28. 已知:线段m,n求作:线段AB,使 . 29.(1)、如图AB∥CD,∠ABE=120°,∠EC D=2 5°,求∠E的度数。
29.(1)、如图AB∥CD,∠ABE=120°,∠EC D=2 5°,求∠E的度数。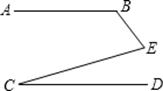 (2)、小亮的一张地图上有A、B、C三个城市,但地图上的C城市被墨迹污染了(如图),但知道∠BAC=∠1,∠ABC=∠2,请你用尺规作图法帮他在如图中确定C城市的具体位置.(用尺规作图,保留作图痕迹,不写作法)
(2)、小亮的一张地图上有A、B、C三个城市,但地图上的C城市被墨迹污染了(如图),但知道∠BAC=∠1,∠ABC=∠2,请你用尺规作图法帮他在如图中确定C城市的具体位置.(用尺规作图,保留作图痕迹,不写作法)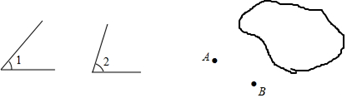 30. 如图,有分别过A、B两个加油站的公路l1、l2相交于点O , 现准备在∠AOB内建一个油库,要求油库的位置点P满足到A、B两个加油站的距离相等,而且油库的位置到两条公路l1、l2的距离也相等.那么油库应该修建在什么位置?在图上标出它的位置(不写作法,保留作图痕迹).
30. 如图,有分别过A、B两个加油站的公路l1、l2相交于点O , 现准备在∠AOB内建一个油库,要求油库的位置点P满足到A、B两个加油站的距离相等,而且油库的位置到两条公路l1、l2的距离也相等.那么油库应该修建在什么位置?在图上标出它的位置(不写作法,保留作图痕迹). 31. 如图,等腰 的顶角 ,请用尺规作图法,在 边上求作一点 ,使得 ∽ .(保留作图痕迹,不写作法)
31. 如图,等腰 的顶角 ,请用尺规作图法,在 边上求作一点 ,使得 ∽ .(保留作图痕迹,不写作法)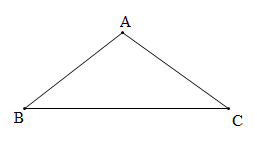 32. 按要求画图,并描述所作线段.
32. 按要求画图,并描述所作线段. (1)、过点A画三角形的高线;(2)、过点B画三角形的中线;(3)、过点C画三角形的角平分线;(4)、作∠D=∠C(尺规作图,不写作法保留作图痕迹).33. 如图,在平面直角坐标系中, 为直角三角形, , ,按要求解答下列问题:
(1)、过点A画三角形的高线;(2)、过点B画三角形的中线;(3)、过点C画三角形的角平分线;(4)、作∠D=∠C(尺规作图,不写作法保留作图痕迹).33. 如图,在平面直角坐标系中, 为直角三角形, , ,按要求解答下列问题: (1)、以原点 为位似中心画出 ,使它与 的相似比为3:2(2)、将 绕点 顺时针旋转90°,画出旋转后的(3)、用点 旋转到点 所经过的路径与 、 围成的扇形做成一个圆锥的侧面(接缝忽略不计),求这个圆锥的高.(保留精确值)
(1)、以原点 为位似中心画出 ,使它与 的相似比为3:2(2)、将 绕点 顺时针旋转90°,画出旋转后的(3)、用点 旋转到点 所经过的路径与 、 围成的扇形做成一个圆锥的侧面(接缝忽略不计),求这个圆锥的高.(保留精确值)