浙教版备考2021年中考数学一轮复习专题33 图形的相似
试卷更新日期:2021-05-09 类型:一轮复习
一、单选题
-
1. 已知 (a≠0,b≠0),下列变形正确的是( )A、 B、 C、 D、2. 下列四组线段中,是成比例线段的是( )A、2cm,3cm,4cm,5cm B、3cm,6cm,0.2dm,5cm C、2cm,4cm,6cm,8cm D、12cm,8cm,15cm,10cm3. 如图,直线l1∥l2∥l3 , 直线AC和DF被l1 , l2 , l3所截,AB=5,BC=6,EF=4,则DE的长为( )
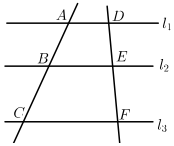 A、2 B、3 C、4 D、4. 下列说法中,正确的是( )A、两个矩形必相似 B、两个含 角的等腰三角形必相似 C、两个菱形必相似 D、两个含 角的直角三角形必相似5. 两个相似多边形的一组对应边分别是3cm和4.5cm,如果它们的周长之和是80cm,那么较大的多边形的周长是( )A、16cm B、32cm C、48cm D、52cm6. 如图,已知△ABC∽△BDC,其中AC=4,CD=2,则BC=( )
A、2 B、3 C、4 D、4. 下列说法中,正确的是( )A、两个矩形必相似 B、两个含 角的等腰三角形必相似 C、两个菱形必相似 D、两个含 角的直角三角形必相似5. 两个相似多边形的一组对应边分别是3cm和4.5cm,如果它们的周长之和是80cm,那么较大的多边形的周长是( )A、16cm B、32cm C、48cm D、52cm6. 如图,已知△ABC∽△BDC,其中AC=4,CD=2,则BC=( )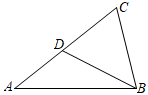 A、2 B、 C、 D、47. 如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC~△AED的是( )
A、2 B、 C、 D、47. 如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC~△AED的是( )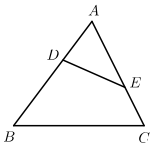 A、∠AED=∠B B、∠ADE=∠C C、 D、8. 如图,在▱ABCD中,若E为DC的中点,AC与BE交于点F,则△EFC与四边形ADEF的面积比为( )
A、∠AED=∠B B、∠ADE=∠C C、 D、8. 如图,在▱ABCD中,若E为DC的中点,AC与BE交于点F,则△EFC与四边形ADEF的面积比为( )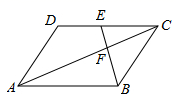 A、1:5 B、1: C、1:4 D、1:79. 如图,为了测量某棵树的高度,小刚用长为2m的竹竿作测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距6m,与树距15m,那么这颗树的高度为( )
A、1:5 B、1: C、1:4 D、1:79. 如图,为了测量某棵树的高度,小刚用长为2m的竹竿作测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距6m,与树距15m,那么这颗树的高度为( )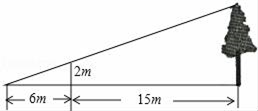 A、5m B、7m C、7.5m D、21m10. 如图,△ABC中,顶点A、B均在第二象限,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C',且△A'B'C'与△ABC的位似比为2:1,设点B的对应点B'的横坐标是3,则点B的横坐标是( )
A、5m B、7m C、7.5m D、21m10. 如图,△ABC中,顶点A、B均在第二象限,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C',且△A'B'C'与△ABC的位似比为2:1,设点B的对应点B'的横坐标是3,则点B的横坐标是( )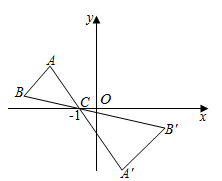 A、 B、﹣2 C、 D、﹣3
A、 B、﹣2 C、 D、﹣3二、填空题
-
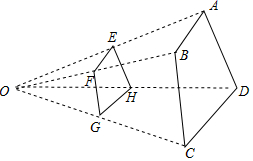
11. 在一幅比例尺是1∶6000000的图纸上,量得两地的图上距离是2厘米,则两地的实际距离是千米.12. 已知线段 的长为4厘米,点P是线段AB的黄金分割点( ),那么线段 的长是厘米.13. 已知 ,则 .14. 如图,四边形 与四边形 位似,位似中心点是O, ,则 .
 15. 如图所示,复印纸的型号有A0 , A1 , A2 , A3 , A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸沿较长边的中点对折,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似,那么这些型号的复印纸的长、宽之比为 .
15. 如图所示,复印纸的型号有A0 , A1 , A2 , A3 , A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸沿较长边的中点对折,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似,那么这些型号的复印纸的长、宽之比为 .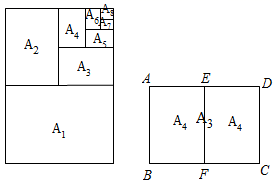 16. 秦九韶的《数书九章》中有一个“峻积验雪”的例子,其原理为:如图,在Rt ABC中,∠C=90°,AC=12,BC=5,AD⊥AB,AD=0.4,过点D作DE AB交CB的延长线于点E,过点B作BF⊥CE交DE于点F,那么BF= .
16. 秦九韶的《数书九章》中有一个“峻积验雪”的例子,其原理为:如图,在Rt ABC中,∠C=90°,AC=12,BC=5,AD⊥AB,AD=0.4,过点D作DE AB交CB的延长线于点E,过点B作BF⊥CE交DE于点F,那么BF= .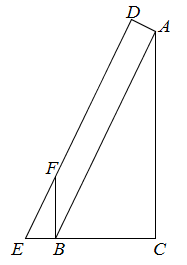
三、解答题
-
17. 如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,连接FD与AC交于点N,求FN:ND的值.
 18. 如图, 中, 两点分别在 上,且 为 的角平分线,若 .
18. 如图, 中, 两点分别在 上,且 为 的角平分线,若 .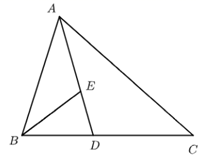 (1)、求证: .(2)、求 与 的面积比.19. 如图,已知△ABC的三个顶点的坐标分别为A(-1,2)、B(-3,0)、C(0,0).
(1)、求证: .(2)、求 与 的面积比.19. 如图,已知△ABC的三个顶点的坐标分别为A(-1,2)、B(-3,0)、C(0,0).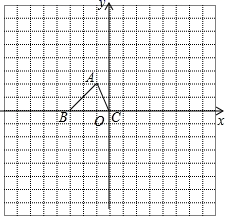
( 1 )以A为中心将△ABC顺时钟旋转90°得△A1B1C1 , 请画出△AB1C1 , 并写现点C1的坐标;
( 2 )以C为位似中心,在x轴下方作△ABC的位似图形△A2B2C2 , 使放大前后位似比为1︰2,请画出图形,并求出△A2B2C2的面积;
( 3 )请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
20. 给你一个锐角三形ABC和任意一条直线MN问题:请同学们利用直线MN.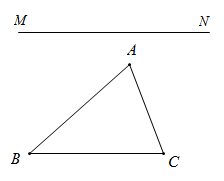 (1)、在 边上或边的延长线作出一个三角形与 相似,并请说明理由;(2)、这样的三角形还能做出几种?利用作图(不保留作图痕迹)简单说明,不必说明理由.21. 如图,为了测量一栋楼的高度 ,小明同学先在操场上 处放一面镜子,向后退到 处,恰好在镜子中看到楼的顶部 ;再将镜子放到 处,然后后退到 处,恰好再次在镜子中看到楼的顶部 ( 在同一条直线上).测得 , ,如果小明眼睛距地面高度 为 ,试确定楼的高度 .
(1)、在 边上或边的延长线作出一个三角形与 相似,并请说明理由;(2)、这样的三角形还能做出几种?利用作图(不保留作图痕迹)简单说明,不必说明理由.21. 如图,为了测量一栋楼的高度 ,小明同学先在操场上 处放一面镜子,向后退到 处,恰好在镜子中看到楼的顶部 ;再将镜子放到 处,然后后退到 处,恰好再次在镜子中看到楼的顶部 ( 在同一条直线上).测得 , ,如果小明眼睛距地面高度 为 ,试确定楼的高度 .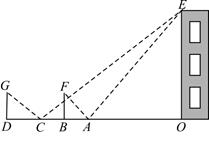 22. 如图,小芳家的落地窗(线段DE)与公路(直线PQ)互相平行,她每天做完作业后都会在点A处向窗外的公路望去.
22. 如图,小芳家的落地窗(线段DE)与公路(直线PQ)互相平行,她每天做完作业后都会在点A处向窗外的公路望去.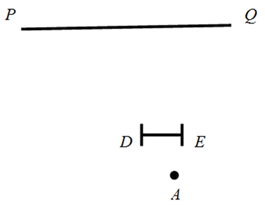 (1)、请在图中画出小芳能看到的那段公路并记为BC.(2)、小芳很想知道点A与公路之间的距离,于是她想到了一个办法.她测出了邻家小彬在公路BC段上走过的时间为10秒,又测量了点A到窗的距离是4米,且窗DE的长为3米,若小彬步行的平均速度为1.2米/秒,请你帮助小芳计算出点A到公路的距离.23. 如图,∠1=∠2, ,求证:∠C=∠D.
(1)、请在图中画出小芳能看到的那段公路并记为BC.(2)、小芳很想知道点A与公路之间的距离,于是她想到了一个办法.她测出了邻家小彬在公路BC段上走过的时间为10秒,又测量了点A到窗的距离是4米,且窗DE的长为3米,若小彬步行的平均速度为1.2米/秒,请你帮助小芳计算出点A到公路的距离.23. 如图,∠1=∠2, ,求证:∠C=∠D.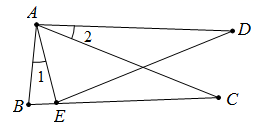 24.(1)、已知 ,求一次函数 所经过的象限;(2)、已知 与 相似,且 的三边长分别为6、8、4, 其中一边长为2,试求 的另外两边长.25. 如图,正方形ABCD的边长为2,E为AB的中点,P是BA延长线上的一点,连接PC交AD于点F,AP=FD
24.(1)、已知 ,求一次函数 所经过的象限;(2)、已知 与 相似,且 的三边长分别为6、8、4, 其中一边长为2,试求 的另外两边长.25. 如图,正方形ABCD的边长为2,E为AB的中点,P是BA延长线上的一点,连接PC交AD于点F,AP=FD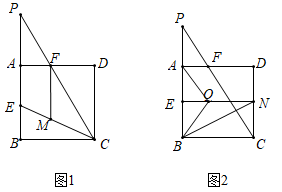 (1)、求 的值(2)、如图1,连接EC,在线段EC上取一点M,使EM=EB,连接MF,求证MF=PF;(3)、如图2,过点E作EN⊥CD于点N,在线段EN上取一点Q,使AQ=AP,连接BQ,BN.将△AQB绕点A旋转,使点Q旋转后的对应点Q'落在边AD上.请判断点B旋转后的对应点B'是否落在线段BN上,并说明理由.
(1)、求 的值(2)、如图1,连接EC,在线段EC上取一点M,使EM=EB,连接MF,求证MF=PF;(3)、如图2,过点E作EN⊥CD于点N,在线段EN上取一点Q,使AQ=AP,连接BQ,BN.将△AQB绕点A旋转,使点Q旋转后的对应点Q'落在边AD上.请判断点B旋转后的对应点B'是否落在线段BN上,并说明理由.
26. 我们知道:如图①,点 把线段 分成两部分,如果 .那么称点 为线段 的黄金分割点.它们的比值为 . (1)、在图①中,若 ,则 的长为 ;(2)、如图②,用边长为 的正方形纸片进行如下操作:对折正方形 得折痕 ,连接 ,将 折叠到 上,点 对应点 ,得折痕 .试说明 是 的黄金分割点;(3)、如图③,小明进一步探究:在边长为 的正方形 的边 上任取点 ,连接 ,作 ,交 于点 ,延长 、 交于点 .他发现当 与 满足某种关系时 、 恰好分别是 、 的黄金分割点.请猜想小明的发现,并说明理由.
(1)、在图①中,若 ,则 的长为 ;(2)、如图②,用边长为 的正方形纸片进行如下操作:对折正方形 得折痕 ,连接 ,将 折叠到 上,点 对应点 ,得折痕 .试说明 是 的黄金分割点;(3)、如图③,小明进一步探究:在边长为 的正方形 的边 上任取点 ,连接 ,作 ,交 于点 ,延长 、 交于点 .他发现当 与 满足某种关系时 、 恰好分别是 、 的黄金分割点.请猜想小明的发现,并说明理由.