浙教版备考2021年中考数学一轮复习专题32 图形的对称、平移与旋转
试卷更新日期:2021-05-09 类型:一轮复习
一、单选题
-
1. 2020年4月7日,中国邮政发行了《众志成城 抗击疫情》邮票一套两枚(图1),以此纪念在抗击新冠肺炎疫情的过程中,中国人民所展现出的“中国精神、中国力量、中国担当”.两枚邮票用一个“众”字型的背景图案巧妙相连,从几何的角度看,这个图案(图2)( )
 A、是中心对称图形而不是轴对称图形 B、是轴对称图形而不是中心对称图形 C、既是轴对称图形又是中心对称图形 D、既不是轴对称图形,又不是中心对称图形2. 点 关于x轴的对称点的坐标为( )A、 B、 C、 D、3. 浙江省积极响应国家“节约资源,保护环境”的号召,利用自身地域环境优势,加强可再生资源——风能的利用。其中,海上风电产业具有技术先导性强、经济体量大和产业关联度大的特点。如图是海上风力发电装置,转子叶片图案绕中心旋转 后能与原图案重合,则 可以取( )
A、是中心对称图形而不是轴对称图形 B、是轴对称图形而不是中心对称图形 C、既是轴对称图形又是中心对称图形 D、既不是轴对称图形,又不是中心对称图形2. 点 关于x轴的对称点的坐标为( )A、 B、 C、 D、3. 浙江省积极响应国家“节约资源,保护环境”的号召,利用自身地域环境优势,加强可再生资源——风能的利用。其中,海上风电产业具有技术先导性强、经济体量大和产业关联度大的特点。如图是海上风力发电装置,转子叶片图案绕中心旋转 后能与原图案重合,则 可以取( ) A、60 B、90 C、120 D、1804. 如图, 中,将 沿 翻折,若 , ,则 多少度( )
A、60 B、90 C、120 D、1804. 如图, 中,将 沿 翻折,若 , ,则 多少度( )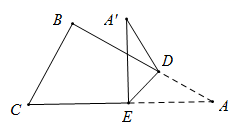 A、60° B、75° C、85° D、90°5. 如图,点M,N在直线l的同侧,小东同学想通过作图在直线l上确定一点Q,使MQ与QN的和最小,那么下面的操作正确的是( )
A、60° B、75° C、85° D、90°5. 如图,点M,N在直线l的同侧,小东同学想通过作图在直线l上确定一点Q,使MQ与QN的和最小,那么下面的操作正确的是( )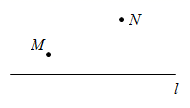 A、
A、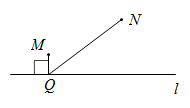 B、
B、 C、
C、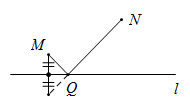 D、
D、 6. 如图,AD是三角形ABC的对称轴,点E、F是AD上的两点,若BD=2,AD=3,则图中阴影部分的面积是( )
6. 如图,AD是三角形ABC的对称轴,点E、F是AD上的两点,若BD=2,AD=3,则图中阴影部分的面积是( )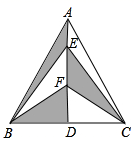 A、3 B、2 C、1 D、47. 如图,图中的小三角形可以由三角形ABC平移得到的有( )
A、3 B、2 C、1 D、47. 如图,图中的小三角形可以由三角形ABC平移得到的有( ) A、5个 B、6个 C、7个 D、8个8. 如图,在方格纸中,三角形 经过变换得到三角形 ,正确的变换是( )
A、5个 B、6个 C、7个 D、8个8. 如图,在方格纸中,三角形 经过变换得到三角形 ,正确的变换是( )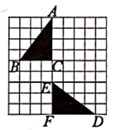 A、把三角形 向下平移4格,再绕点 逆时针方向旋转180° B、把三角形 向下平移5格,再绕点 顺时针方向旋转180° C、把三角形 绕点 逆时针方向旋转90°,再向下平移2格 D、把三角形 绕点 顺时针方向旋转90°,再向下平移5格9. 如图,将 绕点A按逆时针方向旋转 ,得到 ,若点 在线段 的延长线上,则 的度数为( )
A、把三角形 向下平移4格,再绕点 逆时针方向旋转180° B、把三角形 向下平移5格,再绕点 顺时针方向旋转180° C、把三角形 绕点 逆时针方向旋转90°,再向下平移2格 D、把三角形 绕点 顺时针方向旋转90°,再向下平移5格9. 如图,将 绕点A按逆时针方向旋转 ,得到 ,若点 在线段 的延长线上,则 的度数为( ) A、 B、 C、 D、10. 线段 CD 是由线段 AB 平移得到的,点A(-1,4)的对应点为C(4,7) ,则 AB 可以通过以下方式平移到 CD ( )A、先向上平移3个单位,再向左平移5个单位 B、先向左平移5个单位,再下平移3个单位 C、先向上平移3个单位,再右平移5个单位 D、先向右平移5个单位,再向下平移3个单位
A、 B、 C、 D、10. 线段 CD 是由线段 AB 平移得到的,点A(-1,4)的对应点为C(4,7) ,则 AB 可以通过以下方式平移到 CD ( )A、先向上平移3个单位,再向左平移5个单位 B、先向左平移5个单位,再下平移3个单位 C、先向上平移3个单位,再右平移5个单位 D、先向右平移5个单位,再向下平移3个单位二、填空题
-
11. 如图,已知点 ,直线 与两坐标轴分别交于A , B两点,D , E分别是AB , OB上的动点,则 周长的最小值是 .
 12. 如图,已知点 , , , ,连接 , ,将线段 绕着某一点旋转一定角度,使 , 分别与 , 重合,则旋转中心的坐标为.
12. 如图,已知点 , , , ,连接 , ,将线段 绕着某一点旋转一定角度,使 , 分别与 , 重合,则旋转中心的坐标为.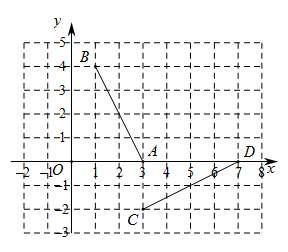 13. 如图,将△OAB绕点O逆时针旋转80°,得到△OCD,若∠A=2∠D=100°,则∠α的度数 .
13. 如图,将△OAB绕点O逆时针旋转80°,得到△OCD,若∠A=2∠D=100°,则∠α的度数 .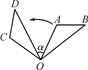 14. 如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为。
14. 如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为。 15. 如图所示,在长为 ,宽为 的草坪上修了一条宽恒为 宽的弯曲小路,则余下草坪的面积为 .
15. 如图所示,在长为 ,宽为 的草坪上修了一条宽恒为 宽的弯曲小路,则余下草坪的面积为 .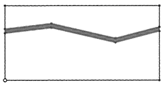 16. 如图,在等边三角形ABC右侧作射线CP, ,点A关于射线CP的对称点为点D,BD交CP于点E,连接AD,AE,若 , ,则 , .
16. 如图,在等边三角形ABC右侧作射线CP, ,点A关于射线CP的对称点为点D,BD交CP于点E,连接AD,AE,若 , ,则 , .
三、解答题
-
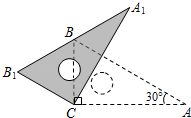
17. 如图,在三角板ABC中,∠ACB=90°,∠A=30°,AC=6,将三角板ABC绕点C逆时针旋转,当起始位置时的点B恰好落在边A1B1上时,求A1B的长
 18. 如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若ED=4cm,FC=lcm,∠BAC=76°,∠EAC=58°
18. 如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若ED=4cm,FC=lcm,∠BAC=76°,∠EAC=58° (1)、求出BF的长度;(2)、求∠CAD的度数;19. 某班级在探究“将军饮马问题”时抽象出数学模型:
(1)、求出BF的长度;(2)、求∠CAD的度数;19. 某班级在探究“将军饮马问题”时抽象出数学模型:直线 同旁有两个定点A、B,在直线 上存在点P,使得PA十PB的值最小.解法:如图1,作点A关于直线 的对称点A',连接A'B, 则A'B与直线 的交点即为P,且PA+PB的最小值为A'B.
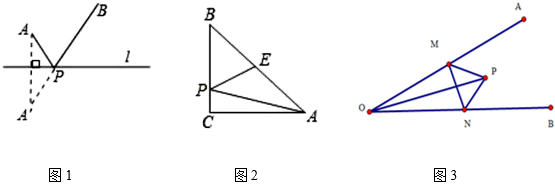
请利用上述模型解决下列问题;
(1)、如图2,ΔABC中,∠C=90°,E是AB的中点,P是BC边上的一动点,作出点P,使得PA+PE的值最小;(2)、如图3,∠AOB=30°,M、N分别为OA、OB上一动点,若OP=5,求ΔPMN的周长的最小值.20. 规定:在平面内,如果一个图形绕一个定点旋转一定的角度α(0°<α≤180°)后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角度α称为这个图形的一个旋转角.例如:正方形绕着两条对角线的交点O旋转90°或180°后,能与自身重合(如图1),所以正方形是旋转对称图形,且有两个旋转角.根据以上规定,回答问题: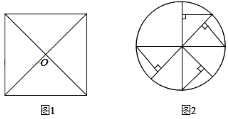 (1)、下列图形是旋转对称图形,但不是中心对称图形的是________;A、矩形 B、正五边形 C、菱形 D、正六边形(2)、下列图形中,是旋转对称图形,且有一个旋转角是60度的有:(填序号);
(1)、下列图形是旋转对称图形,但不是中心对称图形的是________;A、矩形 B、正五边形 C、菱形 D、正六边形(2)、下列图形中,是旋转对称图形,且有一个旋转角是60度的有:(填序号);
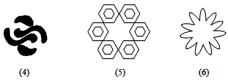 (3)、下列三个命题:①中心对称图形是旋转对称图形;②等腰三角形是旋转对称图形;③圆是旋转对称图形,其中真命题的个数有( )个;A、0 B、1 C、2 D、3(4)、如图2的旋转对称图形由等腰直角三角形和圆构成,旋转角有45°,90°,135°,180°,将图形补充完整.21. 问题情境:
(3)、下列三个命题:①中心对称图形是旋转对称图形;②等腰三角形是旋转对称图形;③圆是旋转对称图形,其中真命题的个数有( )个;A、0 B、1 C、2 D、3(4)、如图2的旋转对称图形由等腰直角三角形和圆构成,旋转角有45°,90°,135°,180°,将图形补充完整.21. 问题情境:如图,在平面直角坐标系中有三点A(x1 , y1),B(x2 , y2),C(x3 , y3),小明在学习中发现,当x1=x2 , AB∥y轴,线段AB的长度为|y1﹣y2|;当y1=y3 , AC∥x轴,线段AC的长度为|x1﹣x3|.
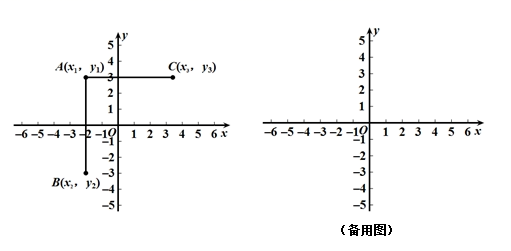 (1)、初步应用
(1)、初步应用若点A(﹣1,1)、B(2,1),则AB∥轴(填“x”或“y”);
(2)、若点C(1,﹣2),CD∥y轴,且点D在x轴上,则CD=;(3)、若点E(﹣3,2),点F(t,﹣4),且EF∥y轴,t=;(4)、拓展探索:已知P(3,﹣3),PQ∥y轴.
若三角形OPQ的面积为3,求满足条件的点Q的坐标.
(5)、若PQ=a,将点Q向右平移b个单位长度到达点M,已知点M在第一象限角平分线上,请直接写出a,b之间满足的关系.22. 阅读材料,并回答下列问题:如图1,以AB为轴,把△ABC翻折180°,可以变换到△ABD的位置;如图2,把△ABC沿射线AC平移,可以变换到△DEF的位置.像这样,其中的一个三角形是另一个三角形经翻折、平移等方法变换成的,这种只改变位置,不改变形状大小的图形变换,叫三角形的全等变换.
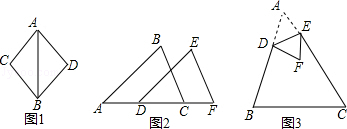 (1)、请你写出一种全等变换的方法(除翻折、平移外).;(2)、如图2,△ABC沿射线AC平移到△DEF,若平移的距离为2,且AC=3,则DC=;(3)、如图3,D、E分别是△ABC的边AB、AC上的点,把△ADE沿DE翻折,当点A落在四边形BCED内部变为F时,则∠F和∠BDF+∠CEF之间的数量关系始终保持不变,请你直接写出它们之间的关系式: .23. 如图,平面直角坐标系中,△ABC的顶点坐标分别为A(4,1),B(3,4),C(1,2).
(1)、请你写出一种全等变换的方法(除翻折、平移外).;(2)、如图2,△ABC沿射线AC平移到△DEF,若平移的距离为2,且AC=3,则DC=;(3)、如图3,D、E分别是△ABC的边AB、AC上的点,把△ADE沿DE翻折,当点A落在四边形BCED内部变为F时,则∠F和∠BDF+∠CEF之间的数量关系始终保持不变,请你直接写出它们之间的关系式: .23. 如图,平面直角坐标系中,△ABC的顶点坐标分别为A(4,1),B(3,4),C(1,2).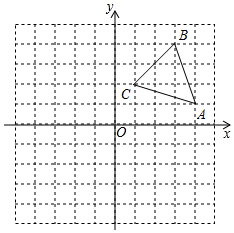 (1)、画出△ABC关于y轴对称的△A1B1C1 , 并写出顶点C1的坐标;(2)、若点P在x轴上,且满足PA+PC1最小,求点P的坐标及PA+PC1的最小值.24. 如图,方格纸上每个小正方形的边长均为1个单位长度,点A、B都在格点上(两条网格线的交点叫格点).
(1)、画出△ABC关于y轴对称的△A1B1C1 , 并写出顶点C1的坐标;(2)、若点P在x轴上,且满足PA+PC1最小,求点P的坐标及PA+PC1的最小值.24. 如图,方格纸上每个小正方形的边长均为1个单位长度,点A、B都在格点上(两条网格线的交点叫格点).
( 1 )将线段AB向上平移两个单位长度,点A的对应点为点 ,点B的对应点为点 ,请画出平移后的线段 ;
( 2 )将线段 绕点 按逆时针方向旋转 ,点 的对应点为点 ,请画出旋转后的线段 ;
( 3 )连接 、 ,求 的面积.
25. (问题解决)
一节数学课上,老师提出了这样一个问题:如图1,点P是正方形ABCD内一点,PA=1,PB=2,PC=3.你能求出∠APB的度数吗?
小明通过观察、分析、思考,形成了如下思路:
(1)、思路一:将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,求出∠APB的度数;思路二:将△APB绕点B顺时针旋转90°,得到△CP'B,连接PP′,求出∠APB的度数.
请参考小明的思路,任选一种写出完整的解答过程.
(2)、【类比探究】
如图2,若点P是正方形ABCD外一点,PA=3,PB=1,PC= ,求∠APB的度数.
26. 如图1,长方形纸片ABCD的两条边AB、BC的长度分别为 、 ,小明它沿对角线AC剪开,得到两张三角形纸片(如图2),再将这两张三角纸片摆成如图3的形状,点A、B、D、E在同一条直线上,且点B与点D重合,点B、F、C也在同一条直线上. (1)、将图3中的△ABC沿射线AE方向平移,使点B与点E重合,点A、C分别对应点M、N , 按要求画出图形,并直接写出平移的距离;(用含 或 的代数式表示)(2)、将图3中的△DEF绕点B逆时针方向旋转60°,点E、F分别对应点P、Q , 按要求画出图形,并直接写出∠ABQ的度数;(3)、将图3中的△ABC沿BC所在直线翻折,点A落在点G处,按要求画出图形,并直接写出GE的长度.(用含 、 的代数式表示)
(1)、将图3中的△ABC沿射线AE方向平移,使点B与点E重合,点A、C分别对应点M、N , 按要求画出图形,并直接写出平移的距离;(用含 或 的代数式表示)(2)、将图3中的△DEF绕点B逆时针方向旋转60°,点E、F分别对应点P、Q , 按要求画出图形,并直接写出∠ABQ的度数;(3)、将图3中的△ABC沿BC所在直线翻折,点A落在点G处,按要求画出图形,并直接写出GE的长度.(用含 、 的代数式表示)