浙教版备考2021年中考数学一轮复习专题31 命题与证明
试卷更新日期:2021-05-09 类型:一轮复习
一、单选题
-
1. 下列语句是命题的是( )
(1)如果两个角的和是90度,那么这两个角互余;(2)请画出两条互相平行的直线;(3)过直线外一点作已知直线的垂线;(4)两点之间,线段最短.A、(2)(3) B、(3)(4) C、(1)(2) D、(1)(4)2. 把命题“等角的余角相等”改写成“如果……那么……”的形式,正确的是( )A、如果两个角互余,那么这两个角相等 B、如果两个角相等,那么这两个角互为余角 C、如果两个角相等,那么这两个角的余角也相等 D、如果两个角互余,那么这两个角的余角相等3. 对于命题“ (a为实数)”,能说明它是假命题的反例是( )A、 B、 C、 D、4. 用反证法证明“a≥b”时应先假设( )A、a≤b B、a>b C、a<b D、a≠b5. 如图,∠BAD=∠BCD=90°,AB=CB,据此可以证明△BAD≌△BCD,证明的依据是 ( ) A、AAS B、ASA C、SAS D、HL6. 下列条件中,不能证明△ABC是直角三角形的是( )A、在△ABC中,∠B=∠C -∠A B、在△ABC中,a2=(b+c) (b-c) C、在△ABC中,∠A:∠B:∠C=3:4:5 D、在△ABC中,a:b:c=4:5:37. 如图,下列推理及所证明的理由都正确的是( )
A、AAS B、ASA C、SAS D、HL6. 下列条件中,不能证明△ABC是直角三角形的是( )A、在△ABC中,∠B=∠C -∠A B、在△ABC中,a2=(b+c) (b-c) C、在△ABC中,∠A:∠B:∠C=3:4:5 D、在△ABC中,a:b:c=4:5:37. 如图,下列推理及所证明的理由都正确的是( )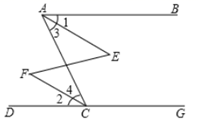 A、若 ,则 ,理由是内错角相等,两直线平行 B、若 ,则 ,理由是两直线平行,内错角相等 C、若 ,则 ,理由是内错角相等,两直线平行 D、若 ,则 ,理由是两直线平行,内错角相等8. 下列命题是真命题的是( )A、如果a+b=0,那么 a,b 互为相反数; B、同位角相等; C、过一点有且只有一条直线与已知直线平行; D、两条直线被第三条直线所截,内错角相等。9. 下列命题的逆命题是假命题的是( )A、直角三角形斜边上的中线等于斜边的一半 B、线段垂直平分线上的点到线段两端的距离相等 C、等腰三角形底边上的高线和中线互相重合 D、两个全等三角形的面积相等10. 下面各图中,不能证明勾股定理正确性的是( )A、
A、若 ,则 ,理由是内错角相等,两直线平行 B、若 ,则 ,理由是两直线平行,内错角相等 C、若 ,则 ,理由是内错角相等,两直线平行 D、若 ,则 ,理由是两直线平行,内错角相等8. 下列命题是真命题的是( )A、如果a+b=0,那么 a,b 互为相反数; B、同位角相等; C、过一点有且只有一条直线与已知直线平行; D、两条直线被第三条直线所截,内错角相等。9. 下列命题的逆命题是假命题的是( )A、直角三角形斜边上的中线等于斜边的一半 B、线段垂直平分线上的点到线段两端的距离相等 C、等腰三角形底边上的高线和中线互相重合 D、两个全等三角形的面积相等10. 下面各图中,不能证明勾股定理正确性的是( )A、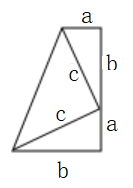 B、
B、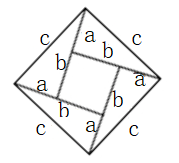 C、
C、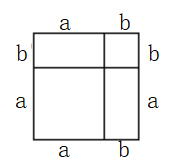 D、
D、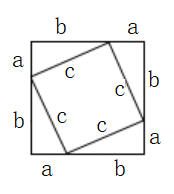
二、填空题
-
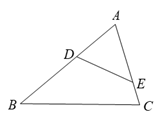
11. 命题“同位角相等,两直线平行”的结论。12. 命题“如果m是整数,那么m一定是有理数”;则它的逆命题是 命题(填写“真”或“假”).13. 请举反例说明命题“对于任意实数x, 的值总是正数”是假命题,你举的反例是 . (写出一个值即可)14. 证明命题“直角三角形中的两个锐角中至少有一个角不小于45°”时,如果用反证法证明,应先假设 .15. 如图,点 , 分别在△ 的 , 边上.只需添加一个条件即可证明△ ∽△ ,这个条件可以是 . (写出一个即可)
 16. 以m=为反例,可以证明“关于x的一元二次方程x2+x+m=0必有实数根”是错误的命题(写出一个m的值即可)。
16. 以m=为反例,可以证明“关于x的一元二次方程x2+x+m=0必有实数根”是错误的命题(写出一个m的值即可)。三、解答题
-
17. 求证:等腰三角形两腰上的中线相等(要求画图,写已知、求证、证明).18. 写出定理“等腰三角形顶角的角平分线和底边上的高线互相重合”的逆命题,并证明这个命题是真命题。
逆命题:。
已知:。
求证: 。
证明:
19. 如图,①AB CD,②BE平分∠ABD,③∠1+∠2=90°,④DE平分∠BDC.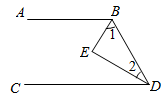 (1)、请以其中三个为条件,第四个为结论,写出一个命题;(2)、判断这个命题是否为真命题,并说明理由.20. 根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形,相似四边形对应边的比叫做相似比.
(1)、请以其中三个为条件,第四个为结论,写出一个命题;(2)、判断这个命题是否为真命题,并说明理由.20. 根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形,相似四边形对应边的比叫做相似比.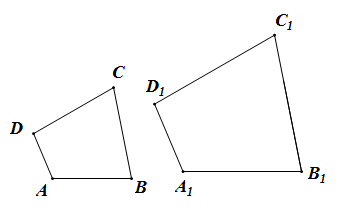 (1)、某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否符合题意(直接在横线上填写“真”或“假”).
(1)、某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否符合题意(直接在横线上填写“真”或“假”).①四条边成比例的两个凸四边形相似;(命题)
②三个角分别相等的两个凸四边形相似;(命题)
③两个大小不同的正方形相似.(命题)
(2)、如图,在四边形 和四边形 中, , ,求证:四边形 与四边形 相似.21. 数学活动实验、猜想与证明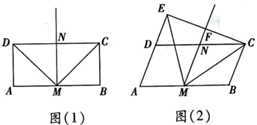 (1)、问题情境
(1)、问题情境数学活动课上,小颖向同学们提出了这样一个问题:如图(1),在矩形ABCD中,AB=2BC,M、N分别是AB,CD的中点,作射线MN,连接MD,MC,请直接写出线段MD与MC之间的数量关系.
(2)、解决问题小彬受此问题启发,将矩形ABCD变为平行四边形,其中∠A为锐角,如图(2),AB=2BC,M,N分别是AB,CD的中点,过点C作CE⊥AD交射线AD于点E,交射线MN于点F,连接ME,MC,则ME=MC,请你证明小彬的结论;
(3)、小丽在小彬结论的基础上提出了一个新问题:∠BME与∠AEM有怎样的数量关系?请你回答小丽提出的这个问题,并证明你的结论.22. (问题原型)如图,在 中,对角线 的垂直平分线 交 于点 ,交 于点 ,交 于点 .求证:四边形 是菱形.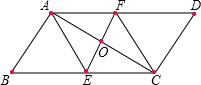
(小海的证法)证明:
是 的垂直平分线,
,(第一步)
,(第二步)
.(第三步)
四边形 是平行四边形.(第四步)
四边形 是菱形. (第五步)
(老师评析)小海利用对角线互相平分证明了四边形 是平行四边形,再利用对角线互相垂直证明它是菱形,可惜有一步错了.
(挑错改错)
(1)、小海的证明过程在第步上开始出现了不正确.(2)、请你根据小海的证题思路写出此题的正确解答过程,23. 请判断下列命题的真假性,若是假命题请举反例说明,若是真命题,请证明.(1)、三角形一条边的两个顶点到这条边的中线所在直线的距离相等.(2)、若 ,则点 在第四象限.
24. 嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证. (1)、已知:如图1,在四边形ABCD中,BC=AD,AB=
(1)、已知:如图1,在四边形ABCD中,BC=AD,AB=求证:四边形ABCD是四边形.
在方框中填空,以补全已知和求证;
(2)、按嘉淇同学的思路写出证明过程;(3)、用文字叙述所证命题的逆命题.25. 以下是某班数学兴趣小组根据课本习题探究数学规律的过程: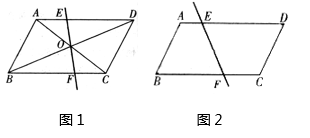 (1)、如图1,已知直线EF是经过平行四边形ABCD对角线交点的任意一条直线,直线EF与AD ,BC分别交于点E ,F.
(1)、如图1,已知直线EF是经过平行四边形ABCD对角线交点的任意一条直线,直线EF与AD ,BC分别交于点E ,F.①求证:四边形ABFE与四边形CDEF的面积相等;
②经过以上证明,可以总结出平行四边形一个一般结论:过平行四边形对角线交点的任意一条直线,.
(2)、探究以上命题的逆命题是否是真命题:①如图2,已知点E ,F分别是平行四边形ABCD的边AD,BC上的两点,(点E ,F不与顶点重合),直线EF将平行四边形ABCD分成面积相等的两部分.
求证:直线EF经过平行四边形ABCD对角线的交点.
②直接回答:经过探究得知(1)②中的命题的逆命题是真命题还是假命题?
26. 问题再现:数形结合是解决数学问题的一种重要的思想方法,借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性,从而可以帮助我们快速解题.初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.
例如:利用图形的几何意义证明完全平方公式.
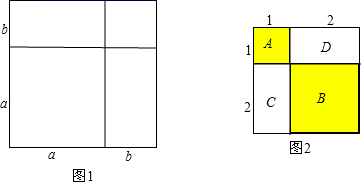
证明:将一个边长为a的正方形的边长增加b,形成两个矩形和两个正方形,如图1:
这个图形的面积可以表示成:
(a+b)2或a2+2ab+b2
∴(a+b)2 =a2+2ab+b2
这就验证了两数和的完全平方公式.
类比解决:
(1)、请你类比上述方法,利用图形的几何意义证明平方差公式.(要求画出图形并写出推理过程)问题提出:如何利用图形几何意义的方法证明:13+23=32?
如图2,A表示1个1×1的正方形,即:1×1×1=13
B表示1个2×2的正方形,C与D恰好可以拼成1个2×2的正方形,因此:B、C、D就可以表示2个2×2的正方形,即:2×2×2=23而A、B、C、D恰好可以拼成一个(1+2)×(1+2)的大正方形.
由此可得:13+23=(1+2)2=32
(2)、请你类比上述推导过程,利用图形的几何意义确定:13+23+33= . (要求写出结论并构造图形写出推证过程).(3)、问题拓广:请用上面的表示几何图形面积的方法探究:13+23+33+…+n3= . (直接写出结论即可,不必写出解题过程)
27. 问题呈现:阿基米德折弦定理:如图1,AB和BC是⊙O的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是 的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.下面是运用“截长法”证明CD=AB+BD的部分证明过程.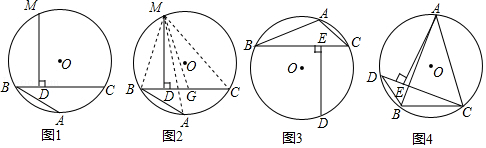
证明:如图2,在CB上截取CG=AB,连接MA,MB,MC和MG
∵M是 的中点,
∴MA=MC
……
(1)、请按照上面的证明思路,写出该证明的剩余部分;(2)、实践应用:①如图3,已知△ABC内接于⊙O,BC>AB>AC,D是 的中点,依据阿基米德折弦定理可得图中某三条线段的等量关系为;
②如图4,已知等腰△ABC内接于⊙O,AB=AC,D为 上一点,连接DB,∠ACD=45°,AE⊥CD于点E,△BCD的周长为4 +2,BC=2,请求出AC的长.