初中数学湘教版九年级下册第四章概率章末检测（提高篇）

试卷更新日期：2021-05-09 类型：单元试卷

进入出卷网下载

一、单选题

1. 下列说法正确的是（）

A、为了解全省中学生的心理健康状况，宜采用普查方式 B、某彩票设“中奖概率为 $\frac{1}{100}$ ”，购买100张彩票就一定会中奖一次 C、某地会发生地震是必然事件 D、若甲组数据的方差S²_甲＝0.1，乙组数据的方差S²_乙＝0.2，则甲组数据比乙组稳定

查看试题解析
2. 下列说法正确的是（）

A、“概率为0.0001的事件”是不可能事件 B、任意掷一枚质地均匀的硬币10次，正面向上的一定是5次 C、“任意画出一个等边三角形，它是轴对称图形”是随机事件 D、“任意画出一个平行四边行，它是中心对称图形”是必然事件

查看试题解析
3. 下列事件是必然事件的是（）

A、如果 $| a | = | b |$ ，那么 $a = b$ B、平分弦的直径垂直于弦，并且平分弦所对的两条弧 C、抛出的篮球会下落 D、三角形的内角和是 $360 °$

查看试题解析
4. 下列叙述正确的是（）

A、“如果a，b是实数，那么a+b=b+a”是不确定事件 B、“某班50位同学中恰有2位同学生日是同一天”是随机事件 C、为了了解一批炮弹的杀伤力，采用普查的调查方式比较合适 D、某种彩票的中奖概率为 $\frac{1}{7}$ ，是指买7张彩票一定有一张中奖

查看试题解析
5. 现有A、B两枚均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6）．用小莉掷A立方体朝上的数字为 $x$ 、小明掷B立方体朝上的数字为 $y$ 来确定点P（ $x ， y$ ），那么他们各掷一次所确定的点P落在已知抛物线 $y = - x^{2} + 4 x$ 上的概率为（）

A、 $\frac{1}{18}$ B、 $\frac{1}{12}$ C、 $\frac{1}{9}$ D、 $\frac{1}{6}$

查看试题解析
6. 如图，ABCD的对角线AC、BD相交于点O，EF、GH过点O，且点E、H在边AB上，点G、F在边CD上，向▱ABCD内部投掷飞镖（每次均落在▱ABCD内，且落在▱ABCD内任何一点的机会均等）恰好落在阴影区域的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{8}$

查看试题解析
7. 如图①所示，平整的地面上有一个不规则图案（图中阴影部分），小明想了解该图案的面积是多少，他采取了以下办法：用一个长为 $5m$ ，宽为 $4m$ 的长方形，将不规则图案围起来，然后在适当位置随机地朝长方形区域扔小球，并记录小球落在不规则图案上的次数（球扔在界线上或长方形区域外不计实验结果），他将若干次有效实验的结果绘制成了②所示的折线统计图，由此他估计不规则图案的面积大约为（）

A、 ${6m}^{2}$ B、 ${7m}^{2}$ C、 ${8m}^{2}$ D、 ${9m}^{2}$

查看试题解析

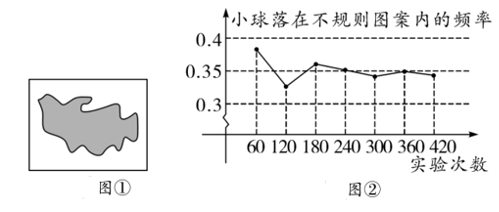8. 某学习小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，绘制了如下的表格，则符合这一结果的实验最有可能的是（　　）

实验次数	100	200	300	500	800	1000	2000
频率	0.365	0.328	0.330	0.334	0.336	0.332	0.333

A、一副去掉大小王的普迺扑克牌洗匀后，从中任抽一张牌的花色是红桃 B、从一个装有2个白球和1个红球的袋子中任取一球，取到红球的概率 C、抛一枚硬币，出现正面的概率 D、抛一个质地均匀的正六面体骰子（六个面上分别标有1，2，3，4，5，6），向上的面点数是5

查看试题解析

9. 某小组做“用频率估计概率”的实验时，绘出的某一结果出现的频率折线图，则符合这一结果的实验可能是（）

A、抛一枚硬币，出现正面朝上 B、掷一个正六面体的骰子，出现3点朝上 C、一副去掉大小王的扑克牌洗匀后，从中任抽一张牌的花色是红桃 D、从一个装有2个红球1个黑球的袋子中任取一球，取到的是黑球

查看试题解析
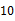10. 甲乙两人轮流在黑板上写下不超过的正整数（每次只能写一个数），规定禁止在黑板上写已经写过的数的约数，最后不能写的为失败者，如果甲写第一个，那么，甲写数字（）时有必胜的策略．

A、10 B、9 C、8 D、6

查看试题解析

二、填空题

11. 袋子里装有4个白球、8个红球、m个黑球，每个球除颜色以外均相同，从袋中任取一个球,若摸到红球的可能最大，摸到白球的可能最小，则m所有可能的取值为(已知m≠4和8)

查看试题解析
12. 写一个你喜欢的实数m的值，使得事件“对于二次函数 $y = \frac{1}{2} x^{2} - (5 m - 3) x + 4$ ，当 $x > 2$ 时，y随x的增大而增大”成为随机事件，这个实数m的值.

查看试题解析
13. 六张正面分别标有数字 $- 1$ 、 $- 2$ 、 $- 3$ 、 $- 4$ 、 $- 5$ 、 $- 6$ 的不透明卡片，它们除数字不同外其余完全相同.将它们背面朝上，洗匀后从中任取一张，以卡片上的数字作为关于x的不等式 $a x + b > 0$ 中的系数a，如果该不等式有正整数解的概率为 $\frac{1}{2}$ ，则实数b的取值范围是.

查看试题解析

14. 公司以3元/

kg

的成本价购进

10000kg

柑橘，并希望出售这些柑橘能够获得12000元利润，在出售柑橘（去掉损坏的柑橘）时，需要先进行“柑橘损坏率”统计，再大约确定每千克柑橘的售价，右面是销售部通过随机取样，得到的“柑橘损坏率”统计表的一部分，由此可估计柑橘完好的概率为（精确到0.1）；从而可大约每千克柑橘的实际售价为元时（精确到0.1），可获得12000元利润．

柑橘总质量 $n /kg$	损坏柑橘质量 $m /kg$	柑橘损坏的频率 $\frac{m}{n}$ （精确到0.001）
…	…	…
250	24.75	0.099
300	30.93	0.103
350	35.12	0.100
450	44.54	0.099
500	50.62	0.101

查看试题解析

15. 在一个不透明的袋中装有12个红球和若干个白球，它们除颜色外都相同 $.$ 从袋中随机摸出一个球，记下颜色后放回，并搅均，不断重复上述的试验共5000次，其中2000次摸到红球，请估计袋中大约有白球个 $.$

查看试题解析
16. 在平面直角坐标系中,作OOAB,其中三个顶点分别是O(0,0),B(1,1),A( $x$ , $y$ ),其中点A,O,B不在同一直线上且-2≤ $x$ ≤2,-2≤ $y$ ≤2, $x$ , $y$ 均为整数，则所作OOAB为直角三角形的概率是.

查看试题解析

三、解答题

17. 乒乓球是我国的国球，比赛采用单局11分制，是一种世界流行的球类体育项目，比赛分团体、单打、双打等数种在某站公开赛中，某直播平台同时直播4场男单四分之一比赛，四场比赛的球桌号分别为“T₁”、“T₂”、“T₃”、“T₄”（假设4场比赛同时开始），小宁和父亲准备一同观看其中的某一场比赛，但两人的意见不统一，于是采用抽签的方式决定，抽签规则如下：将正面分别写有数字“1、“2”、“3”、“4”的四张卡片（除数字不同外，其余均相同，数字“1”、“2”、“3”、“4”分别对应球桌号（“T₁”、“T₂”、“T₃”、“T₄”（背面朝上洗匀，父亲先从中随机抽取一张，小宁再从剩下的3张卡片中随机抽取一张，比较两人所抽卡片上的数字，观看较大的数字对应球桌的比赛

(1)、下列事件中属于必然事件的是
A ．抽到的是小宁最终想要看的一场比赛的球桌号

B ．抽到的是父亲最终想要看的一场比赛的球桌号

C ．小宁和父亲抽到同一个球桌号

D ．小宁和父亲抽到的球桌号不一样

(2)、用列表法或树状图法求小宁和父亲最终观看“T₄”球桌比赛的概率

查看试题解析
18. 有一个可自由转动的转盘，被分成了4个相同的扇形，分别标有数1，2，3，4（如图所示），另有一个不透明的口袋装有分别标有数0，1，3的三个小球（除数字不同外，其余都相同），小亮转动一次转盘，停止后指针指向某一扇形（指针指向两个扇形的交线时，当作指向右边的扇形），扇形内的数是小亮的幸运数，小红任意摸出一个小球，小球上的数是小红的吉祥数，然后计算这两个数的积.

(1)、请你用画树状图或列表的方法，求这两个数的积为0的概率；

(2)、小亮与小红做游戏，规则是：若这两个数的积为奇数，小亮赢；否则，小红赢.你认为该游戏公平吗？为什么？如果不公平，请你修改该游戏规则，使游戏公平.

查看试题解析
19. 在一个不透明的盒子中放有四张卡片，每张卡片上写有一个实数，分别为2， $\sqrt{2} - 1$ ， $\sqrt{2} + 1$ ， $1. ($ 卡片除了实数不同外，其余均相同 $)$

(1)、从盒子中随机抽取一张卡片，请直接写出卡片上的实数是有理数的概率；

(2)、将卡片揺匀后先随机抽出一张，再从剩下的卡片中随机抽出一张，然后将抽取的两张卡片上的实数相乘，请你用列表法或树状图 $($ 树形图 $)$ 法，求抽取的两张卡片上的实数之积为整数的概率.

查看试题解析

20. 新冠疫情期间，某校有“录播”和“直播”两种教学方式供学生自主选择其中一种进行居家线上学习.为了了解该校学生线上学习参与度情况，从选择这两种教学方式的学生中，分别随机抽取50名进行调查，调查结果如表（数据分组包含左端值不包含右端值）.

	$0 ~ 20 %$	$20 % ~ 50 %$	$50 % ~ 80 %$	$80 % ~ 100 %$
录播	5	18	14	13
直播	2	15	21	12

(1)、从选择教学方式为“录播”的学生中任意抽取1名学生，试估计该生的参与度不低于

50 %

的概率；

(2)、若该校共有1200名学生，选择“录播”和“直播”的人数之比为

3 ： 5

，试估计选择“录播”或“直播”参与度均在

20 %

以下的共有多少人？

查看试题解析

21. 如图，地面上有一个不规则的封闭图形ABCD，为求得它的面积，小明在此封闭图形内画出一个半径为2米的圆后，在附近闭上眼睛向封闭图形内掷小石子（可把小石子近似地看成点），记录如下：

掷小石子落在不规则图形内的总次数	50	150	300	…
小石子落在圆内（含圆上）的次数m	20	59	123	…
小石子落在圆外的阴影部分（含外缘）的次数n	29	91	176	…

(1)、当投掷的次数很大时，则m：n的值越来越接近（结果精确到0.1）

(2)、若以小石子所落的有效区域为总数（即m+n），则随着投掷次数的增大，小石子落在圆内（含圆上）的频率值稳定在附近（结果精确到0.1）；

(3)、请你利用（2）中所得频率的值，估计整个封闭图形ABCD的面积是多少平方米？（结果保留π）

查看试题解析

22. 一粒木质中国象棋棋子“車”，它的正面雕刻一个“車”字，它的反面是平的，将棋子从一定高度下抛，落地反弹后可能是“車”字面朝上，也可能是“車”字朝下.由于棋子的两面不均匀，为了估计“車”字朝上的机会，某实验小组做了棋子下抛实验，并把实验数据整理如下：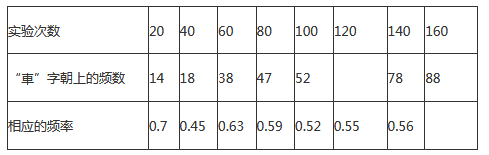

(1)、请将表中数据补充完整，并画出折线统计图中剩余部分.

(2)、如果实验继续进行下去，根据上表数据，这个实验的频率将接近于该事件发生的机会，请估计这个机会约是多少？

(3)、在（2）的基础上，进一步估计：将该“車”字棋子，按照实验要求连续抛2次，则刚好使“車”字一次字面朝上，一次朝下的可能性为多少？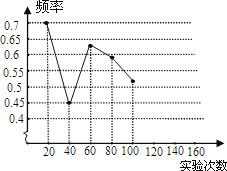

查看试题解析

23. 王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀，让若干学生进行摸球实验，每次摸出一个球(有放回)，下表是活动进行中的一组统计数据。

摸球的次数n	100	150	200	500	800	1000
摸到黑球的次数m	23	31	60	130	203	251
摸到黑球的频率mn	0.23	0.21	0.30	0.26	0.253

(1)、补全上表中的有关数据，根据上表数据估计从袋中摸出一个球是黑球的概率是；（保留小数点后两位）

(2)、估算袋中白球的个数；

(3)、在(2)的条件下，若小强同学有放回地连续两次摸球，用画树形图或列表的方法计算他两次都摸出白球的概率.

查看试题解析

24. 如图，放在直角坐标系中的正方形ABCD边长为4，现做如下实验：抛掷一枚均匀的正四面体骰子（它有四个顶点，各顶点的点数分别是1至4这四个数字中一个），每个顶点朝上的机会是相同的，连续抛掷两次，将骰子朝上的顶点数作为直角坐标中P点的坐标）第一次的点数作横坐标，第二次的点数作纵坐标）．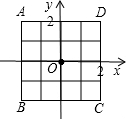

(1)、求P点落在正方形ABCD面上（含正方形内部和边界）的概率．

(2)、将正方形ABCD平移整数个单位，则是否存在一种平移，使点P落在正方形ABCD面上的概率为 $\frac{3}{4}$ ，若存在，指出其中的一种平移方式；若不存在，请说明理？

查看试题解析

初中数学湘教版九年级下册第四章 概率 章末检测（提高篇）

一、单选题

二、填空题

三、解答题

初中数学湘教版九年级下册第四章概率章末检测（提高篇）