初中数学湘教版七年级下册第五章 轴对称与旋转 章末检测(提高篇)
试卷更新日期:2021-05-09 类型:单元试卷
一、单选题
-
1. 将一张长方形的纸片对折,然后用笔尖在上面扎出字母“B”,再把它展开铺平后,你可以看到的图形是( )A、
 B、
B、 C、
C、 D、
D、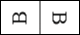 2. 如图,在方格纸中,三角形ABC经过变换得到三角形DEF,正确变换的是( )
2. 如图,在方格纸中,三角形ABC经过变换得到三角形DEF,正确变换的是( ) A、把三角形ABC向下平移4格,再绕着点C逆时针方向旋转 B、把三角形ABC向下平移5格,再绕着点C顺时针方向旋转 C、把三角形ABC绕着点C逆时针方向旋转 ,再向下平移2格 D、把三角形ABC绕着点C顺时针方向旋转 ,再向下平移5格3.
A、把三角形ABC向下平移4格,再绕着点C逆时针方向旋转 B、把三角形ABC向下平移5格,再绕着点C顺时针方向旋转 C、把三角形ABC绕着点C逆时针方向旋转 ,再向下平移2格 D、把三角形ABC绕着点C顺时针方向旋转 ,再向下平移5格3.观察下图,在下列四种图形变换中,该图案不包含的变换是( )
 A、平移 B、轴对称 C、旋转 D、位似4. 下列所示的图案中,可以由一个“基本图形”连续旋转45°得到的是( )
A、平移 B、轴对称 C、旋转 D、位似4. 下列所示的图案中,可以由一个“基本图形”连续旋转45°得到的是( )
A、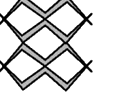 B、
B、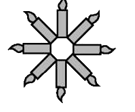 C、
C、 D、
D、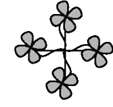 5. 如图,是由大小一样的小正方形组成的网格,△ABC的三个顶点均落在小正方形的顶点上.在网格上能画出的三个顶点都落在小正方形的顶点上,且与△ABC成轴对称的三角形共有( )
5. 如图,是由大小一样的小正方形组成的网格,△ABC的三个顶点均落在小正方形的顶点上.在网格上能画出的三个顶点都落在小正方形的顶点上,且与△ABC成轴对称的三角形共有( )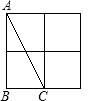 A、5个 B、4个 C、3个 D、2个6. 如图,是一个纸折的小风车模型,将它绕着旋转中心旋转下列哪个度数后不能与原图形重合.( )
A、5个 B、4个 C、3个 D、2个6. 如图,是一个纸折的小风车模型,将它绕着旋转中心旋转下列哪个度数后不能与原图形重合.( ) A、 B、 C、 D、7. 将一图形绕着点O顺时针方向旋转60°,再绕着点O逆时针方向旋转170°,这时如果使图形回到原来的位置,需要将图形绕着点O( )A、顺时针旋转230° B、逆时针旋转110° C、顺时针旋转110° D、逆时针旋转230°8. 如图,是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出,该球最后落入1号袋,经过反射的次数是( )
A、 B、 C、 D、7. 将一图形绕着点O顺时针方向旋转60°,再绕着点O逆时针方向旋转170°,这时如果使图形回到原来的位置,需要将图形绕着点O( )A、顺时针旋转230° B、逆时针旋转110° C、顺时针旋转110° D、逆时针旋转230°8. 如图,是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出,该球最后落入1号袋,经过反射的次数是( )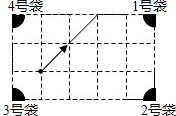 A、4次 B、5次 C、6次 D、7次9. 如图中的四个图案,四位同学分别说出了它们的形成过程,其中说得不正确的是( )
A、4次 B、5次 C、6次 D、7次9. 如图中的四个图案,四位同学分别说出了它们的形成过程,其中说得不正确的是( )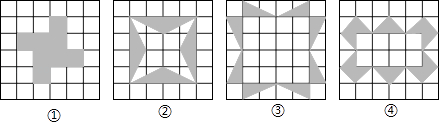 A、图①是一个长方形绕着图形的中心按逆时针旋转90°,180°和270°所得 B、图②可由一个钝角三角形绕着图形的中心按同一方向旋转90°,180°和270°形成 C、图③可以看作以正方形的一条对角线所在直线为对称轴翻折所得 D、图④可以看作由长方形的一边的垂直平分线为对称轴翻折而成10. 一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行.如图2:当∠CAE=60°时,BC∥DE.则∠CAE(0° ∠CAE 180°)其它所有可能符合条件的度数为( )
A、图①是一个长方形绕着图形的中心按逆时针旋转90°,180°和270°所得 B、图②可由一个钝角三角形绕着图形的中心按同一方向旋转90°,180°和270°形成 C、图③可以看作以正方形的一条对角线所在直线为对称轴翻折所得 D、图④可以看作由长方形的一边的垂直平分线为对称轴翻折而成10. 一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行.如图2:当∠CAE=60°时,BC∥DE.则∠CAE(0° ∠CAE 180°)其它所有可能符合条件的度数为( )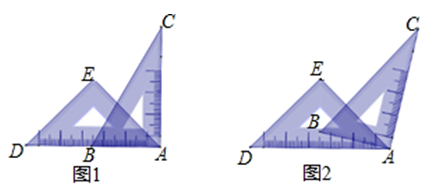 A、75°和105° B、90 °和135° C、90°,105°和150° D、90°,120°和150°
A、75°和105° B、90 °和135° C、90°,105°和150° D、90°,120°和150°二、填空题
-
11. 如图,将△ABC沿着DE对折,点A落到A′处,若∠BDA′+∠CEA′=70°,则∠A= .
 12. 把一张长方形纸片按图中那样折叠后,若得到∠BGD′=40°,则∠C′FE=°.
12. 把一张长方形纸片按图中那样折叠后,若得到∠BGD′=40°,则∠C′FE=°. 13. 如图,点P在∠AOB内,点M、N分别是点P关于OA、OB的对称点,若△PEF的周长为17,则MN的长为 .
13. 如图,点P在∠AOB内,点M、N分别是点P关于OA、OB的对称点,若△PEF的周长为17,则MN的长为 .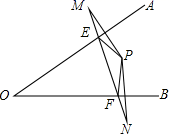 14. 如图是由三个小正方形组成的图形请你在图中补画一个小正方形使补画后的图形为轴对称图形,共有种补法.
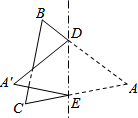
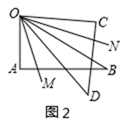
14. 如图是由三个小正方形组成的图形请你在图中补画一个小正方形使补画后的图形为轴对称图形,共有种补法. 15. 一副三角板AOB与COD如图摆放,且∠A=∠C=90°,∠AOB=60°,∠COD=45°,ON平分∠COB,OM平分∠AOD.当三角板COD绕O点顺时针旋转(从图1到图2).设图1、图2中的∠NOM的度数分别为α,β, =度.
15. 一副三角板AOB与COD如图摆放,且∠A=∠C=90°,∠AOB=60°,∠COD=45°,ON平分∠COB,OM平分∠AOD.当三角板COD绕O点顺时针旋转(从图1到图2).设图1、图2中的∠NOM的度数分别为α,β, =度.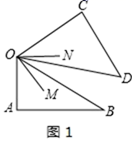
 16. 如图,把一副三角板如图摆放,点E在边AC上,将图中的△ABC绕点A按每秒5°速度沿顺时针方向旋转一周,在旋转的过程中,在第秒时,边BC恰好与边DE平行.
16. 如图,把一副三角板如图摆放,点E在边AC上,将图中的△ABC绕点A按每秒5°速度沿顺时针方向旋转一周,在旋转的过程中,在第秒时,边BC恰好与边DE平行.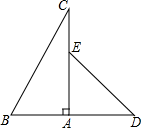
三、解答题
-
17. 在3×3的正方形格点图中,△ABC和△DEF是关于某条直线成轴对称的两个格点三角形,现给出了△ABC , 在下面的图中画出5个符合条件的△DEF , 并画出对称轴.
 18. 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,O,M也在格点上.
18. 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,O,M也在格点上.
①画出△ABC先向右平移5个单位长度,再向下平移5个单位长度得到的△A'B'C';
②画出△ABC关于直线OM对称的△A1B1C1;
③画出△ABC绕点O按顺时针方向旋转90°后所得的△A2B2C2;
④△A1B1C1与△A2B2C2组成的图形是轴对称图形吗?如果是轴对称图形,请画出对称轴.
19. 在如图的正方形网格中,每个小正方形的边长都是单位1,三角形ABC的顶点均在格点上. (1)、①画出三角形ABC绕C点按逆时针方向旋转90°后得到的三角形AB1C1;
(1)、①画出三角形ABC绕C点按逆时针方向旋转90°后得到的三角形AB1C1;②画出三角形A2B2C2 , 使三角形A2B2C2和三角形AB1C1关于直线a成轴对称;
(2)、线段AB变换到A1B1的过程中扫过的区域面积为 .20. 课本在介绍了画轴对称图形的一种方法之后,指出“画轴对称图形,这只是图案设计的一种方法”.其实,设计轴对称图形的方法也并不只是课本中介绍的一种.把几个轴对称图形,或者关于某条直线成轴对称的几对图形适当进行组合,也是设计轴对称图形比较常用的办法.下面是几个这样产生出来的轴对称图形的例子. (1)、上面几个轴对称图形都是几个轴对称图形组合的产物,但具体做法又可以看作是两种不同情况,请指出是哪两种情况.(2)、请按本题说明的途径设计两个轴对称图形.21. 尺规作图:把如图(实线部分)补成以虚线m为对称轴的轴对称图形,你会得到一只美丽蝴蝶的图案.(不用写作法,保留作图痕迹).
(1)、上面几个轴对称图形都是几个轴对称图形组合的产物,但具体做法又可以看作是两种不同情况,请指出是哪两种情况.(2)、请按本题说明的途径设计两个轴对称图形.21. 尺规作图:把如图(实线部分)补成以虚线m为对称轴的轴对称图形,你会得到一只美丽蝴蝶的图案.(不用写作法,保留作图痕迹).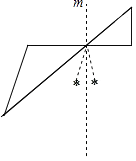 22. 长江汛期即将来临,为r便于夜间查看江水及两岸河堤的情况,防汛指挥部在一危险地带两岸各安置了一探照灯(如图1),∠BAN=45°.灯A射线自AM顺时针旋转至AN便立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是3度/秒,灯B转动的速度是1度/秒.假定这一带长江两岸河堤是平行的,即PQ∥MN.如图2,两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,求∠BAC与∠BCD的比值,并说明理由。
22. 长江汛期即将来临,为r便于夜间查看江水及两岸河堤的情况,防汛指挥部在一危险地带两岸各安置了一探照灯(如图1),∠BAN=45°.灯A射线自AM顺时针旋转至AN便立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是3度/秒,灯B转动的速度是1度/秒.假定这一带长江两岸河堤是平行的,即PQ∥MN.如图2,两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,求∠BAC与∠BCD的比值,并说明理由。 23. 如图1,点O为直线AB上一点,点C是位于直线AB上方的一点,且∠BOC=20° , 将一个含60°三角板(∠POQ=60°)顶点放在点O处,一边OP与射线OA重合,点Q在直线AB的上方 .
23. 如图1,点O为直线AB上一点,点C是位于直线AB上方的一点,且∠BOC=20° , 将一个含60°三角板(∠POQ=60°)顶点放在点O处,一边OP与射线OA重合,点Q在直线AB的上方 .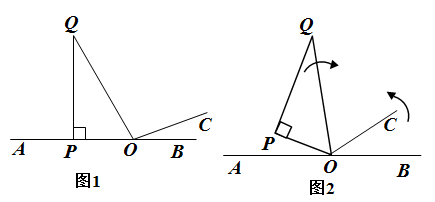 (1)、∠QOC=°(2)、如图2,现将图1位置中三角板△OPQ绕点O沿顺时针方向每秒转动8° , 射线OC绕点O沿逆时针方向每秒转动12° , 设转动的时间为t秒,当点Q、点C有一点位于直线AB上时,转动停止.
(1)、∠QOC=°(2)、如图2,现将图1位置中三角板△OPQ绕点O沿顺时针方向每秒转动8° , 射线OC绕点O沿逆时针方向每秒转动12° , 设转动的时间为t秒,当点Q、点C有一点位于直线AB上时,转动停止.①当线段OQ与射线OC重合时,求t的值;
②当t=时,OP⊥OC .
24. 如图,将两个完全一样的等腰直角三角尺如图叠放,∠B=∠D=90°,∠AOB=∠DOC=45°,使公共顶点与直线OF上的点O重合,∠DOF=10°,∠AOD=70°.规定三角板从现有位置绕着点O顺时针旋转α度记为<+,α>,逆时针旋转α度记为<-,α>(0≤α≤360).如三角板AOB绕着点O顺时针旋转30度后的位置记作<+,30>,绕着点O逆时针旋转15度后的位置记作<-,15>.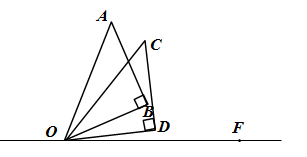 (1)、∠BOF=°;(2)、把三角板AOB绕点O旋转,使OB⊥OF,则旋转后三角板AOB位置记作;(3)、若三角板AOB绕点O按每秒4°的速度旋转至<+,α>,同时三角板COD绕点O以每秒1°的速度旋转至<-,β>.设旋转时间为t秒,请求出当∠DOB=10°时t的值.
(1)、∠BOF=°;(2)、把三角板AOB绕点O旋转,使OB⊥OF,则旋转后三角板AOB位置记作;(3)、若三角板AOB绕点O按每秒4°的速度旋转至<+,α>,同时三角板COD绕点O以每秒1°的速度旋转至<-,β>.设旋转时间为t秒,请求出当∠DOB=10°时t的值.