河南省新乡市2021届高三理数第三次模拟考试试卷

试卷更新日期：2021-05-08 类型：高考模拟

进入出卷网下载

一、单选题

1. 若复数 $z = \frac{m i}{1 + i} (m \in R)$ ，且 $| z | = \sqrt{2}$ ，则 $m =$ （）

A、±1 B、 $\pm \sqrt{3}$ C、 $\pm \sqrt{2}$ D、±2

查看试题解析
2. 已知集合 $A = {x | x^{2} - 3 x - 10 \leq 0}$ ， $B = {x | x \in N}$ ，则集合 $A \cap B$ 的元素个数是（）

A、6 B、7 C、8 D、5

查看试题解析
3. 若 $\lg \tan α = 1$ ， $\log_{3} \tan β = 2$ ，则 $\tan (α - β) =$ （）

A、 $- \frac{19}{89}$ B、 $\frac{1}{91}$ C、 $- \frac{1}{89}$ D、 $- \frac{1}{91}$

查看试题解析
4. 为庆祝建党100周年，某校组织了一场以“不忘初心，牢记使命”为主题的演讲比赛，该校高一年级某班准备从7名男生，5名女生中任选2人参加该校组织的演讲比赛，则参赛的2人中至少有1名女生的概率是（）

A、 $\frac{7}{22}$ B、 $\frac{9}{22}$ C、 $\frac{15}{22}$ D、 $\frac{17}{22}$

查看试题解析
5. 若函数 $f (x) = 3^{x} - \frac{3}{x}$ ，则“ $a > 1$ ”是“ $f (a) > 0$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
6. 在三楼锥 $P - A B C$ 中， $D$ 为 $B C$ 的中点， $P A ⊥$ 底面 $A B C$ ， $A B ⊥ A C$ ， $A B = 4$ ， $A C = 2$ ，若 $P D$ 与底面 $A B C$ 所成角为45°，则三棱锥 $P - A B C$ 的体积为（）

A、 $\sqrt{5}$ B、 $\frac{4 \sqrt{5}}{3}$ C、 $4 \sqrt{5}$ D、 $\frac{5 \sqrt{5}}{4}$

查看试题解析
7. 若正整数 $N$ 除以正整数 $m$ 得到的余数为 $n$ ，则记为 $N \equiv n (\mod m)$ ，例如 $30 \equiv 6 (\mod 8)$ .如图所示的程序框图的算法源于我国古代的《中国剩余定理》.执行该程序框图，则输出的 $n =$ （）

A、109 B、121 C、107 D、124

查看试题解析
8. 已知函数 $f (x) = 4 \sin (2 x - \frac{π}{6}) + 1$ 的定义域是 $[0 ， m]$ ，值域为 $[- 1 ， 5]$ ，则 $m$ 的最大值是（）

A、 $\frac{π}{3}$ B、 $\frac{2 π}{3}$ C、 $\frac{π}{6}$ D、 $\frac{5 π}{6}$

查看试题解析
9. 某冷饮店的日销售额 $y$ (单位：元)与当天的最高气温 $x$ (单位：℃， $20 \leq x \leq 40$ )的关系式为 $y = \frac{19}{10} x^{2} - \frac{1}{30} x^{3}$ ，则该冷饮店的日销售额的最大值约为（）

A、907元 B、910元 C、915元 D、920元

查看试题解析
10. 某三棱锥的三视图如图所示.则该三棱锥外接球的半径是（）

A、 $\sqrt{5}$ B、2 C、 $\sqrt{6}$ D、 $2 \sqrt{2}$

查看试题解析
11. 已知抛物线 $M ： x^{2} = 2 p y (p > 0)$ 的焦点为 $F$ ，过点 $F$ 且斜率为 $\frac{5}{12}$ 的直线 $l$ 与抛物线 $M$ 交于 $A$ ､ $B$ 两点(点 $A$ 在第二象限)，则 $\frac{| A F |}{| B F |} =$ （）

A、 $\frac{5}{13}$ B、 $\frac{4}{13}$ C、 $\frac{5}{9}$ D、 $\frac{4}{9}$

查看试题解析
12. 已知函数 $f (x) = | x^{2} + m x | (m > 0)$ .当 $a \in (1 ， 4)$ 时.关于 $x$ 的方程 $f (x) - a | x - 1 | = 0$ 恰有两个不同的实根，则 $m$ 的取值范围是（）

A、 $(0 ， 2]$ B、 $(1 ， 3]$ C、 $(0 ， 3]$ D、 $(1 ， 4]$

查看试题解析

二、填空题

13. 已知向量 $\vec{a} = (1, x)$ ， $\vec{b} = (x, 4)$ ，则当 $| \vec{a} | = 2$ 时， $| \vec{b} | =$ .

查看试题解析
14. 设 $x$ ， $y$ 满足约束条件 ${\begin{array}{l} y \geq 1 \\ x - y \geq 0 \\ 2 x + y \leq 9 \end{array}$ ，则 $z = x + y$ 的最大值是.

查看试题解析
15. 在 $△ A B C$ 中，内角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ .下列各组条件中使得 $△ A B C$ 有两解的是.(填入所有符合的条件的序号)
① $a = 2 \sqrt{3}$ ， $b = 4$ ， $\cos A = - \frac{1}{4}$

② $a = 2 \sqrt{3}$ ， $b = 8$ ， $\cos A = \frac{\sqrt{13}}{4}$

③ $a = \sqrt{15}$ ， $b = 4$ ， $A = \frac{π}{3}$

④ $a = 2 \sqrt{3}$ ， $b = 4$ ， $A = \frac{π}{6}$

查看试题解析
16. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 虚轴的一个顶点为 $D$ ，直线 $x = 2 a$ 与 $C$ 交于 $A$ ， $B$ 两点，若 $△ A B D$ 的垂心在 $C$ 的一条渐近线上，则 $C$ 的离心率为.

查看试题解析

三、解答题

17. 如图，在四棱锥 $P - A B C D$ 中， $P A ⊥$ 平面 $A B C D$ ，四边形 $A B C D$ 是平行四边形， $∠ A B C = 45 °$ ， $M$ ， $N$ 分别是棱 $B C$ ， $P C$ 的中点，且 $A B = A C = P A$ .

(1)、证明：平面 $A M N ⊥$ 平面 $P A D$ .

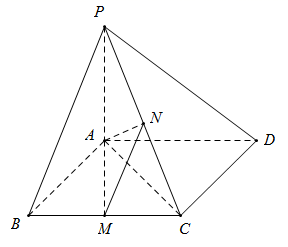(2)、求平面 $A M N$ 与平面 $P A B$ 所成二面角的正弦值.

查看试题解析

18. 某奶茶店推出一款新品奶茶，每杯成本为4元，售价为6元，如果当天卖不完，剩下的奶茶只能倒掉，奶茶店记录了60天这款新品奶茶的日需求量，整理得下表：

日需求量杯数	20	25	30	35	40	45	50
天数	5	5	10	15	10	10	5

以这60天记录中各需求量的频率作为各需求量发生的概率.

(1)、若奶茶店一天准备了35杯这款新品奶茶，用

ξ

表示当天销售这款新品奶茶的利润(单位：元)，求

ξ

的分布列和数学期望；

(2)、假设奶茶店每天准备的这款新晶奶茶杯数都是5的倍数，有顾客建议店主每天准备40杯这款新品奶茶，你认为店主应该接受这个建议吗？请说明理由.

查看试题解析

19. 已知等比数列 ${a_{n}}$ 的第2项和第5项分别为2和16，数列 ${2 n + 3}$ 的前 $n$ 项和为 $S_{n}$ .

(1)、求 $a_{n}$ ， $S_{n}$ ；

(2)、求数列 ${a_{n} \cdot (S_{n} + 2)}$ 的前 $n$ 项和 $T_{n}$ .

查看试题解析
20. 已知椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的长轴长为4，离心率为 $\frac{\sqrt{3}}{2}$ .

(1)、求椭圆 $C$ 的方程；

(2)、直线 $l$ 与椭圆 $C$ 交于 $A$ ， $B$ 两点， $O$ 为坐标原点， $\vec{O A} + \vec{O B} = 2 \vec{O M}$ ，若 $| \vec{O M} | = 1$ ，求 $△ A O B$ 面积的最大值.

查看试题解析
21. 已知函数 $f (x) = a \ln x + x$ .

(1)、讨论 $f (x)$ 的单调性.

(2)、当 $a = 1$ 时，证明： $x f (x) < e^{x}$ .

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，直线 $l_{1}$ 的参数方程为 ${\begin{array}{l} x = - \sqrt{3} + t \\ y = k t \end{array}$ ( $t$ 为参数)，直线 $l_{2}$ 的参数议程为 ${\begin{array}{l} x = \sqrt{3} - s \\ y = \frac{s}{3 k} \end{array}$ ( $s$ 为参数)，直线 $l_{1}$ 与 $l_{2}$ 的交点为 $P$ ，以坐标原点 $O$ 为极点， $x$ 轴正半轴为极轴建立极坐标系，曲线 $C_{1}$ 的极坐标方程为 $\sqrt{2} ρ \sin (θ + \frac{π}{4}) = 1$ .

(1)、求点 $P$ 的轨迹 $C$ 的普通方程；

(2)、若曲线 $C_{1}$ 与曲线 $C$ 相交于 $M$ ， $N$ 两点，点 $Q$ 的直角坐标为 $(1, 0)$ ，求 $\frac{1}{| Q M |} + \frac{1}{| Q N |}$ 的值.

查看试题解析
23. 已知函数 $f (x) = | x + 2 | - | x - 1 |$ .

(1)、求不等式 $f (x) \geq x + 1$ 的解集.

(2)、若函数 $f (x)$ 的最大值为 $m$ ，设 $a > 0$ ， $b > 0$ ，且 $a + b = m$ ，证明： $\frac{b^{2}}{a + 2} + \frac{a^{2}}{b + 1} \geq \frac{3}{2}$ .

查看试题解析