上海市长横学区2020-2021学年七年级下学期数学期中试卷
试卷更新日期:2021-05-08 类型:期中考试
一、选择题(本大题共6题,每题3分,满分18分)
-
1. 其中,无理数的个数是( ).A、2 B、3 C、4 D、52. 以下计算正确的是( ).A、 B、 C、 D、3. 如图,下列说法中错误的是( ).
 A、∠FBC和∠ACE是内错角 B、∠ABD和∠ACH是同位角 C、∠GBD和∠HCE是同位角 D、∠GBC和∠BCE是同旁内角4. 如图,直线 ,AC⊥BC,AC交直线BC于点C,∠1=60°,则∠2的度数是( ).
A、∠FBC和∠ACE是内错角 B、∠ABD和∠ACH是同位角 C、∠GBD和∠HCE是同位角 D、∠GBC和∠BCE是同旁内角4. 如图,直线 ,AC⊥BC,AC交直线BC于点C,∠1=60°,则∠2的度数是( ).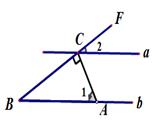 A、50° B、45° C、35° D、30°5. 如图所知,已知OA⊥BC,垂足为点A,联结OB,下列说法:①线段OB是O、B两点的距离;②线段AB的长度表示点B到OA的距离;③因为OA⊥BC,所以∠CAO=90°;④线段OA的长度是点O到直线BC上点的最短距离.其中错误的有( ).
A、50° B、45° C、35° D、30°5. 如图所知,已知OA⊥BC,垂足为点A,联结OB,下列说法:①线段OB是O、B两点的距离;②线段AB的长度表示点B到OA的距离;③因为OA⊥BC,所以∠CAO=90°;④线段OA的长度是点O到直线BC上点的最短距离.其中错误的有( ).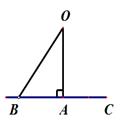 A、1个 B、2个 C、3个 D、4个6. 如图,直线 都与直线 相交,其中不能判定 的条件是( ).
A、1个 B、2个 C、3个 D、4个6. 如图,直线 都与直线 相交,其中不能判定 的条件是( ). A、∠1=∠2 B、∠3=∠6 C、∠1=∠4 D、∠5+∠8=180°
A、∠1=∠2 B、∠3=∠6 C、∠1=∠4 D、∠5+∠8=180°二、填空题(本大题共12题,每题2分,满分24分)
-
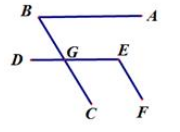
7. 64的平方根是 .8. 若 ( 为连续整数),那么 的值为.9. 的四次方根是.10. 近似数 精确到位,有效数字是.11. 用幂的形式表示: =.12. 比较大小: ;(选填“>”或“<”)13. 化简: =.14. 数轴上表示1、 的对应点分别为点A、点B,若点B关于点A的对称点为点C,则点C所表示的数为.15. 如图,∠ABC与∠DEF的边BC与DE相交于点G,且BA//DE,BC//EF,如果∠B=54°,那么∠E=.
 16. 如图,已知直线AB、CD相交与点O,如果∠BOD=40°,OA平分∠COE,那么∠DOE=.
16. 如图,已知直线AB、CD相交与点O,如果∠BOD=40°,OA平分∠COE,那么∠DOE=.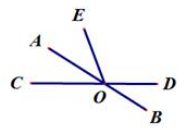 17. 如图,已知∠1=∠2,AD=2BC,∆ABC的面积为3,则∆CAD的面积为.
17. 如图,已知∠1=∠2,AD=2BC,∆ABC的面积为3,则∆CAD的面积为.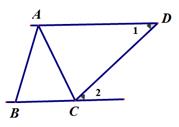 18. 如图,一条公路修到湖边时,需绕弯绕湖而过,如果第一次拐角∠A是120°,第二次拐角∠B是150°,第三次拐角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C为.
18. 如图,一条公路修到湖边时,需绕弯绕湖而过,如果第一次拐角∠A是120°,第二次拐角∠B是150°,第三次拐角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C为.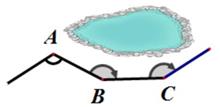
三、简答题(本大题共6题,每题5分,满分30分)
-
19. 计算:20. 计算:21. 计算:22. 计算:23. 计算:24. 利用幂的运算性质计算:
四、解答题(本大题共4题,6分+6分+7分+9分=28分)
-
25. 如图,直线AE、CE分别被直线EF、AC所截,已知∠1=∠2,AB平分∠EAC,
CD平分∠ACG,将下列证明AB//CD的过程及理由填写完整.
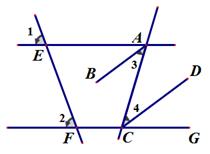
证明:因为∠1=∠2,
所以//(),
所以∠EAC=∠ACG(),
因为AB平分∠EAC,CD平分∠ACG,
所以= ,= ,
所以= ,
所以AB//CD( ).
26. 如图,已知CD//BE,且∠D=∠E,试说明AD//CE的理由. 27. 如图,已知直线AB//EF,AB//CD,∠ABE=50°,EC平分∠BEF,求∠DCE的度数.
27. 如图,已知直线AB//EF,AB//CD,∠ABE=50°,EC平分∠BEF,求∠DCE的度数.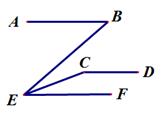 28. 问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
28. 问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.小明的思路是:如图2,过P作PE∥AB,通过平行线性质来求∠APC.
 (1)、按小明的思路,易求得∠APC的度数为度;(2)、如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(1)、按小明的思路,易求得∠APC的度数为度;(2)、如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?请说明理由;
(3)、在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.