安徽省合肥包河区2020-2021学年七年级下学期数学期中试卷
试卷更新日期:2021-05-08 类型:期中考试
一、选择题(每小题3分,满分30分)
-
1. 下列实数是无理数的是( )A、 B、3.14 C、 D、2. 下列运算正确的是( )A、(-3mn)2=-6m2n2 B、(x2y)3=x5y3 C、(xy)2÷(-xy)=-xy D、(a-b)(-a-b)=a2-b23. a、b都是实数,且a< b,则下列不等式正确的是( )A、a+x > b+x B、1-a< 1-b C、5a < 5b D、 >4. 某商品的标价比成本价高m%,根据市场行情,该商品需降价n%出售,为了不亏本,则m、n应满足( )A、(1+m%)(1+n%)≥1 B、(1+m%)(1-n%)≥1 C、(1-m%)(1+n%)≥1 D、(1-m%)(1-n%)≥15. 与 最接近的整数是( )A、3 B、4 C、5 D、76. 若(x+8)(x-1)=x2+mx+n任意x都成立,则m+n=( )A、-8 B、-1 C、1 D、87. 不等式组 的解集在数轴上表示为( )A、
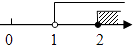 B、
B、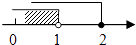 C、
C、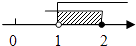 D、
D、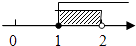 8. 已知正数x满足 ,则 的值为( )A、31 B、16 C、8 D、49. 若关于x、y的二元一次方程组 的解满足x+y> 0,则m的取值范围是( )A、m > -2 B、m < -2 C、m > -1 D、m < -110. 设[x)表示大于x的最小整数,如[3)=4,[-1.2)=-1,下列结论:①[0)=0;②[x)-x的最小值是0;③[x)-x的最大值是1;④存在实数x,使[x)-x=0.5成立,其中正确的是( )A、①② B、③④ C、①②③ D、②③④.
8. 已知正数x满足 ,则 的值为( )A、31 B、16 C、8 D、49. 若关于x、y的二元一次方程组 的解满足x+y> 0,则m的取值范围是( )A、m > -2 B、m < -2 C、m > -1 D、m < -110. 设[x)表示大于x的最小整数,如[3)=4,[-1.2)=-1,下列结论:①[0)=0;②[x)-x的最小值是0;③[x)-x的最大值是1;④存在实数x,使[x)-x=0.5成立,其中正确的是( )A、①② B、③④ C、①②③ D、②③④.二、填空题(本题共6小题,每小题3分,共18分)
-
11. PM2.5是指大气中直径小于或等于0.0000025米的颗粒物,将0.0000025用科学记数法表示为12. 若|2a-7|=7-2a,则a=(请写出一个符合条件的正无理数).13. 若不等式(1-a)x > 1-a的解集是x< 1,则a的取值范围是14. 如果3-6x的立方根是-3,则2x+6的算术平方根为15. 若不等式组 无解,则m的取值范围是16. 《庄子天下篇》中“一尺之棰,日取其半,万世不竭”的意思是:一根一尺的木棍,如果每天截取它的一半,永远也取不完,如图,由图易得: ,那么
=。

三、解答题(本题共6小题,共52分)
-
17.(1)、计算: ;(2)、解不等式: ,并将其解集在数轴上表示出来。
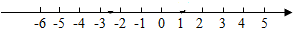 18. 阅读材料图中是小明同学的作业,老师看了后找来小明问道,小明同学,你标在数轴上的两个点,对应体重的两个无理数是吗,小明点点头,老师又说,你这两个无理数对应的点找得非常准确,遗憾的是没有完成全部解答,请你帮小明同学完成本次作业请把实数0,-π,-2, ,1表示在数轴上,并比较它们的大小(用<号连接).
18. 阅读材料图中是小明同学的作业,老师看了后找来小明问道,小明同学,你标在数轴上的两个点,对应体重的两个无理数是吗,小明点点头,老师又说,你这两个无理数对应的点找得非常准确,遗憾的是没有完成全部解答,请你帮小明同学完成本次作业请把实数0,-π,-2, ,1表示在数轴上,并比较它们的大小(用<号连接). 19. 当x=-2,y=2时,先化简,再求(2x+y)2+(x-y)(x+y)-5x(x-y)的值20. 观察下列各式:
19. 当x=-2,y=2时,先化简,再求(2x+y)2+(x-y)(x+y)-5x(x-y)的值20. 观察下列各式:①1×2-0×3=2; ②2×3-1×4=2; ③3×4-2×5=2; ④4×5-3×6=2;……
(1)、请按上述规律写出第⑤个式子:;(2)、请按上述规律写出第n个等式(用含字母的式子表示);(3)、你认为(2)中所写的等式一定成立吗?请说明理由.21. 包河区计划对某校园内面积为3600m2的区域进行绿化。经招标,由甲、乙两个工程队来完成。已知甲队4天能完成绿化的民间等于乙队8天完成绿化的面积,甲队3天能完成绿化的面积比乙队5天能完成绿化面积多50m2(1)、求甲、乙两个工程队每天能完成绿化的面积;(2)、若甲队每天绿化费用是1.2万元,乙队每天绿化费用为0.5万元,要使这次绿化的总费用不超过40万元,则至少应安排乙工程队绿化多少天?22. 如图是用总长为8米的篱笆(图中所有线段)围成的区域。此区域由面积均相等的三块长方形①②③拼成的,若FC=EB=X米.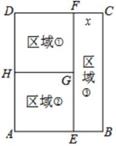 (1)、用含x的代数式表示AB、BC的长;(2)、用含x的代数式表示长方形ABCD的面积(要求化简)
(1)、用含x的代数式表示AB、BC的长;(2)、用含x的代数式表示长方形ABCD的面积(要求化简)