上海市浦东新区2020-2021学年八年级下学期数学期中试卷

试卷更新日期：2021-05-08 类型：期中考试

进入出卷网下载

一、选择题（4×3分=12分）

1. 直线 $y = 3 x - 3$ 的截距是（）

A、-3 B、-1 C、1 D、3

查看试题解析
2. 如果关于 $x$ 的方程 $(a - 3) x = 2021$ 有解，那么实数 $a$ 的取值范围是（）

A、 $a < 3$ B、 $a = 3$ C、 $a > 3$ D、 $a \neq 3$

查看试题解析
3. 一个多边形的内角和是外角和的2倍，这个多边形是（　　）

A、三角形 B、四边形 C、五边形 D、六边形

查看试题解析
4. 一次函数y＝kx﹣k（k＜0）的图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题（14×2分=28分）

5. 已知一次函数 $f (x) = 3 x + 2$ ，那么 $f (- 2) =$

查看试题解析
6. 已知函数 $y = - 3 x + 7$ ，当 $x > 2$ 时，函数值 $y$ 的取值范围是

查看试题解析
7. 如果将直线 $y = 2 x$ 向上平移1个单位，那么平移后所得直线的表达式是．

查看试题解析
8. 分式方程 $\frac{x^{2} - 4}{x - 2} = 0$ 的解是．

查看试题解析
9. 方程 $\sqrt{x + 2} \cdot \sqrt{x - 2} = 0$ 的解是．

查看试题解析
10. 二项方程 $2 x^{3} + 54 = 0$ 的解是．

查看试题解析
11. 用换元法解方程 $\frac{x^{2} - 1}{x} - \frac{x}{x^{2} - 1} = 1$ 时，如果设 $\frac{x}{x^{2} - 1} = y$ ，那么所得到的关于 $y$ 的整式方程为．

查看试题解析
12. 当m= ，方程 $\frac{3}{x} + \frac{6}{x - 1} = \frac{x + m}{x (x - 1)}$ 会产生增根.

查看试题解析
13. 已知：点 $A (- 1 ， a)$ 、 $B (1 ， b)$ 在函数 $y = - 2 x + m$ 的图像上，则 $a$ $b$ （在横线上填写“ $>$ ”或“=”或“ $<$ ”）.

查看试题解析
14. 某商品原价为180元，连续两次提价后售价为300元，且每次提价的百分率相等，设每次提价的百分率为x，依题意可列方程.

查看试题解析
15. 已知一个多边形的每个外角都是30°，那么这个多边形的内角和为．

查看试题解析
16. 已知一次函数y＝kx+b的图象不经过第三象限，那么函数值y随自变量x的值增大而（填“增大”或“减小”）．

查看试题解析
17. 已知一次函数y＝kx+b（k、b是常数）的图象如图所示，那么关于x的不等式kx+b≥0的解集是．

查看试题解析
18. 如图，将△ABC的边AB绕着点A顺时针旋转α（0°＜α＜90°）得到AB′，边AC绕着点A逆时针旋转β（0°＜β＜90°）得到AC′，联结B′C′，当α+β＝60°时，我们称△AB′C′是△ABC的“双旋三角形”，如果等边△ABC的边长为a ，那么它所得的“双旋三角形”中B′C′＝（用含a的代数式表示）．

查看试题解析

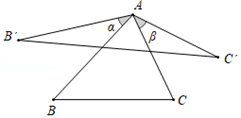
三、解答题（19～24题，每题6分；第25、26题每题7分，共计50分）

19. 解方程： $\frac{x + 2}{x - 2} - \frac{1}{x + 2} = \frac{16}{x^{2} - 4}$

查看试题解析
20. 解方程：
$\sqrt{x + 2} = - x$

查看试题解析
21. 解方程组： ${\begin{cases} x^{2} - x y - 2 y^{2} = 0 \\ 2 x + y = 3 \end{cases}$

查看试题解析
22. 解关于x的方程： $b x^{2} = x^{2} + 1 (b \neq 1)$

查看试题解析
23. 已知直线 $y = k x + b$ 经过点A（1，1），B(-1，-3)

(1)、求此直线的解析式；

(2)、若P点在该直线上，P到y轴的距离为2，求P的坐标．

查看试题解析
24. 小李家离某书店6千米，他从家中出发步行到该书店，由于返回时步行速度比去时步行速度每小时慢了1千米，结果返回时多用了半小时，求小李去书店时的步行速度．

查看试题解析
25. 观察方程①：x＋ $\frac{3}{x}$ ＝4，方程②：x＋ $\frac{8}{x}$ ＝6，方程③：x＋ $\frac{15}{x}$ ＝8．

(1)、方程①的根为：；方程②的根为：；方程③的根为：；

(2)、按规律写出第四个方程：；此分式方程的根为：；

(3)、写出第n个方程（系数用n表示）：；此方程解是：．

查看试题解析
26. 为传播“绿色出行，低碳生活”的理念，小贾同学的爸爸从家里出发，骑自行车去图书馆看书，图中表达的是小贾的爸爸行驶的路程 $y$ （米）与行驶时间 $x$ （分钟）的变化关系．

(1)、求线段 $B C$ 所表达的函数关系式；

(2)、如果小贾与爸爸同时从家里出发，小贾始终以速度120米/分行驶，当小贾与爸爸相遇时，求小贾的行驶时间；

(3)、如果小贾与爸爸同时从家里出发，小贾的行驶速度是 $v$ 米/分，且在途中与爸爸恰好相遇两次（不包括家、图书馆两地），请直接写出 $v$ 的取值范围．

查看试题解析

四、综合题（本题满分10分，第一小题2分，第二小题5分，第三小题3分）

27. 已知一次函数 $y = - \frac{3}{4} x + 6$ 的图像与坐标轴交于 $A$ 、 $B$ 点（如图）， $A E$ 平分 $∠ B A O$ ，交 $x$ 轴于点 $E$ .

(1)、求点 $B$ 的坐标；

(2)、先求点E坐标，然后在 $x$ 轴上找点P，使得 $Δ A E P$ 为等腰三角形，请直接写出符合条件的点P坐标；

(3)、过点 $B$ 作 $B F ⊥ A E$ ，垂足为 $F$ ，联结OF ，试判断△OFB的形状，并求△OFB的面积.

查看试题解析