上海市闵行区2020-2021学年八年级下学期数学期中试卷
试卷更新日期:2021-05-08 类型:期中考试
一、选择题:(共6题,每题3分,满分18分)
-
1. 下列函数是一次函数的是( )A、 B、 C、 D、2. 已知直线 经过两点(a,-1)和(b,7),则a,b的大小关系是( )A、a<b B、a>b C、a=b D、无法确定3. 已知菱形的周长是40cm,两条对角线的长度比为3:4,那么两条对角线的长分别为( )A、6cm,8cm B、3cm,4cm C、12cm,16cm D、24cm,32cm4. 函数 与函数 (k≠0)再同一直角坐标系中的大致图像可能是( )A、
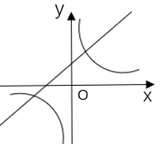 B、
B、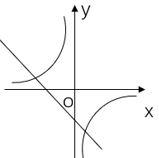 C、
C、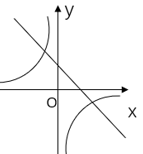 D、
D、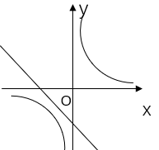 5. 一专业户计划在一定时间内种植蔬菜60亩,在实际播种时,每天比原计划多种了3亩,故提前1天完成,那么求实际播种时间为 x 天的方程是( )A、 B、 C、 D、6. 下列方程一定有实数根的是( )A、 B、 C、 D、
5. 一专业户计划在一定时间内种植蔬菜60亩,在实际播种时,每天比原计划多种了3亩,故提前1天完成,那么求实际播种时间为 x 天的方程是( )A、 B、 C、 D、6. 下列方程一定有实数根的是( )A、 B、 C、 D、二、填空题:(共10题,每题2分,满分20分)
-
7. 已知函数 ,当 时, 的取值范围是8. 一次函数 可由一次函数 向平移个单位得到。9. 已知一次函数 与 轴的交点坐标的横坐标是3,且平行于函数 ,那么这个一次函数解析式是10. 如果一个多边形内角和是外角和的2倍,那么这个多边形的边数是11. 解分式方程 时,设 ,则方程化为关于 的整式方程是12. 已知关于 的分式方程 有增根 =1.则k=13. 某公司成立3年以来,积极向国家上缴利税,有第一年的200万元,增长到第三年的800万元,已知每年的增长率相同,则平均每年增长的百分数是14. 如图,矩形ABCD中,AB=2,CD=3,对角线AC的垂直平分线分别交AD,BC于点E,F,连接CE,则CE的长为
 15. 我们把一条直线上满足横坐标是纵坐标2倍的点称为“加倍点”,那么直线 上的“加倍点”坐标是16. 如图,△ABC中,点O是AB边上的一个动点,过点O做直线MN∥BC,直线MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,设OC的长为x,EF的长为y,那么y关于x的函数关系式是
15. 我们把一条直线上满足横坐标是纵坐标2倍的点称为“加倍点”,那么直线 上的“加倍点”坐标是16. 如图,△ABC中,点O是AB边上的一个动点,过点O做直线MN∥BC,直线MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,设OC的长为x,EF的长为y,那么y关于x的函数关系式是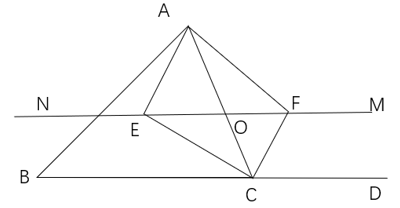
三、简答题(共6题,满分36分)
-
17. 解方程: + =18. 解方程:19. 解方程组:20. 解方程组:21. 直线 与直线 的图像交于点(2,-4),且在y轴上的截距是-6,求:(1)、这两个函数关系式(2)、这两条直线与x轴围成的三角形面积。22. 如图,在平行四边形ABCD中,AB=AE
 (1)、求证:AC=ED(2)、若AE平分∠DAB,∠EAC=25°,求∠ACD的度数。
(1)、求证:AC=ED(2)、若AE平分∠DAB,∠EAC=25°,求∠ACD的度数。四、解答题(共3题,23,24题各8分,25题10分,满分26分)
-
23. 随着虹桥综合交通枢纽的 开工建设,“大虹桥”将成为上海“后世博”阶段重要的经济亮点,上海将形成东有“大浦东”,西有“大虹桥”的“双引擎”格局。现有一个工程,要整修一段全长为1200米的道路,为了尽量减少施工对城市交通造成的影响,实际工作效率比原来提高20%,结果提前4小时完成任务,求原计划每小时修路的长度是多少米?24. 如图,边长为6的正方形OABC的顶点O在原点,点A,点C在x轴和y轴的正半轴上,直线 与两坐标轴分别交于点E和 点F,与正方形的边AB、BC分别交于点M和点N。
 (1)、请直接写出点M和点N的坐标;(2)、求点O到MN的距离;(3)、求∠AMO+∠CNO的度数25. 如图,直线l1:y=-x+m 与y轴交于点A,直线l2:y=2x+n 与y轴交于点C,与x轴交于点D,且它们都经过点B(2,2),
(1)、请直接写出点M和点N的坐标;(2)、求点O到MN的距离;(3)、求∠AMO+∠CNO的度数25. 如图,直线l1:y=-x+m 与y轴交于点A,直线l2:y=2x+n 与y轴交于点C,与x轴交于点D,且它们都经过点B(2,2),
 (备用图)(1)、求点A和点D坐标(2)、过点A作BC的平行线交x轴于点E,求点E坐标(3)、在(2)的条件下,直线 上是否存在一动点P,使△EDP是等腰三角形?若存在,请直接写出P点坐标;若不存在,请说明理由。
(备用图)(1)、求点A和点D坐标(2)、过点A作BC的平行线交x轴于点E,求点E坐标(3)、在(2)的条件下,直线 上是否存在一动点P,使△EDP是等腰三角形?若存在,请直接写出P点坐标;若不存在,请说明理由。