上海市闵行区2021年中考数学二模试卷
试卷更新日期:2021-05-08 类型:中考模拟
一、单选题
-
1. 下列运算中,运算结果正确的是( )A、 B、 C、 D、2. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、3. 在平面直角坐标系中,一次函数y=kx+b的图象如图所示,则k和b的取值范围是( )
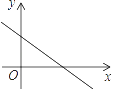 A、k>0,b>0 B、k>0,b<0 C、k<0,b>0 D、k<0,b<04. 如果一组数据为 ,0,1,0,0,那么下列说法错误的是( )A、这组数据的方差是0 B、这组数据的众数是0 C、这组数据的中位数是0 D、这组数据的平均数是05. 下列命题中,真命题是( )A、有两个内角是 的四边形是矩形 B、一组邻边互相垂直的菱形是正方形 C、对角线相互垂直的梯形是等腰梯形 D、两组内角相等的四边形是平行四边形6. 如图,在 中, , , ,点P在边 上, 的半径为3, 的半径为2,如果 和 相交,那么线段 长的取值范围是( )
A、k>0,b>0 B、k>0,b<0 C、k<0,b>0 D、k<0,b<04. 如果一组数据为 ,0,1,0,0,那么下列说法错误的是( )A、这组数据的方差是0 B、这组数据的众数是0 C、这组数据的中位数是0 D、这组数据的平均数是05. 下列命题中,真命题是( )A、有两个内角是 的四边形是矩形 B、一组邻边互相垂直的菱形是正方形 C、对角线相互垂直的梯形是等腰梯形 D、两组内角相等的四边形是平行四边形6. 如图,在 中, , , ,点P在边 上, 的半径为3, 的半径为2,如果 和 相交,那么线段 长的取值范围是( )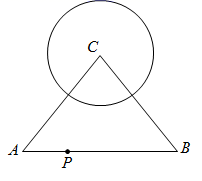 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 的倒数是 .8. 在实数范围内分解因式: .9. 已知函数 ,那么 .10. 方程 的解是 .11. 二元一次方程组 的解是 .12. 如果关于x的一元二次方程 有两个相等的实数根,那么 .13. 已知点 和 均在反比例函数 的图像上,且 ,那么 (填<,>或=)14. 布袋中有五个大小一样的球,分别写有 , , , , 这五个实数,从布袋中任意摸出一个球,那么摸出写有无理数的球的概率为 .15. 为了解全区104000个小学生家庭是否有校内课后服务需求,随机调查了4000个小学生家庭,结果发现有2800个小学生家庭有校内课后服务需求,那么估计该区约有个小学生家庭有校内课后服务需求.16. 《九章算术》中记载了一种测距的方法.如图,有座塔在河流北岸的点E处,一棵树位于河流南岸的点A处,从点A处开始,在河流南岸立4根标杆,以这4根标杆为顶点,组成边长为10米的正方形 ,且A,D,E三点在一条直线上,在标杆B处观察塔E,视线 与边 相交于点F,如果测得 米,那么塔与树的距离 为米.
 17. 如图,在 中, , ,点D为 中点,将 沿直线 翻折后,点A落在点E处,设 , ,那么向量 用向量 , 表示为 .
17. 如图,在 中, , ,点D为 中点,将 沿直线 翻折后,点A落在点E处,设 , ,那么向量 用向量 , 表示为 . 18. 对于任意三角形,如果存在一个菱形,使得这个菱形的一条边与三角形的一条边重合,且三角形的这条边所对的顶点在菱形的这条边的对边上,那么称这个菱形为该三角形的“最优覆盖菱形”.问题:如图,在 中, , ,且 的面积为m,如果 存在“最优覆盖菱形”为菱形 ,那么m的取值范围是 .
18. 对于任意三角形,如果存在一个菱形,使得这个菱形的一条边与三角形的一条边重合,且三角形的这条边所对的顶点在菱形的这条边的对边上,那么称这个菱形为该三角形的“最优覆盖菱形”.问题:如图,在 中, , ,且 的面积为m,如果 存在“最优覆盖菱形”为菱形 ,那么m的取值范围是 .
三、解答题
-
19. 计算: .20. 解不等式组: .并把解集在数轴上表示出来.
 21. 如图,四边形 是平行四边形,联结 , .
21. 如图,四边形 是平行四边形,联结 , . (1)、求 的度数.(2)、求 的值.22. 在疫情防控常态化背景下,每周需要对面积为4800平方米的仓库进行一次全面消毒工作.最初采用人工操作完成消毒任务.为提高效率采用机器人消毒,机器人消毒每分钟消毒面积比人工操作多60平方米,并且提前40分钟完成消毒任务.求人工操作每分钟消毒面积为多少平方米.23. 如图,在梯形 中, ,过点A作 ,垂足为点E,过点E作 ,垂足为点F,联结 ,且 平分 .
(1)、求 的度数.(2)、求 的值.22. 在疫情防控常态化背景下,每周需要对面积为4800平方米的仓库进行一次全面消毒工作.最初采用人工操作完成消毒任务.为提高效率采用机器人消毒,机器人消毒每分钟消毒面积比人工操作多60平方米,并且提前40分钟完成消毒任务.求人工操作每分钟消毒面积为多少平方米.23. 如图,在梯形 中, ,过点A作 ,垂足为点E,过点E作 ,垂足为点F,联结 ,且 平分 . (1)、求证: ;(2)、联结 , 与 交于点G,当 时,求证 .24. 在平面直角坐标系 中,抛物线 经过点 ,顶点为点B,对称轴为直线 ,且对称轴与x轴交于点C.直线 ,经过点A,与线段 交于点E.(1)、求抛物线 的表达式;(2)、联结 、 .当 的面积为3时,求直线 的表达式;(3)、在(2)的条件下,设点D为y轴上的一点,联结 、 ,当 时,求 的余切值.25. 如图,在矩形 中, , ,点P在边 上(点P与端点B、C不重合),以P为圆心, 为半径作圆,圆P与射线 的另一个交点为点E,直线 与射线 交于点G.点M为线段 的中点,联结 .设 .
(1)、求证: ;(2)、联结 , 与 交于点G,当 时,求证 .24. 在平面直角坐标系 中,抛物线 经过点 ,顶点为点B,对称轴为直线 ,且对称轴与x轴交于点C.直线 ,经过点A,与线段 交于点E.(1)、求抛物线 的表达式;(2)、联结 、 .当 的面积为3时,求直线 的表达式;(3)、在(2)的条件下,设点D为y轴上的一点,联结 、 ,当 时,求 的余切值.25. 如图,在矩形 中, , ,点P在边 上(点P与端点B、C不重合),以P为圆心, 为半径作圆,圆P与射线 的另一个交点为点E,直线 与射线 交于点G.点M为线段 的中点,联结 .设 .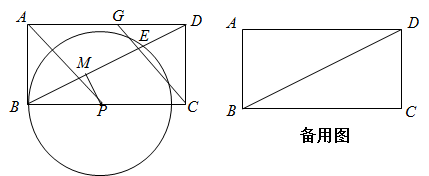 (1)、求y关于x的函数解析式,并写出该函数的定义域;(2)、联结 ,当 时,求x的值;(3)、如果射线 与圆P的另一个公共点为点F,当 为直角三角形时,求 的面积.
(1)、求y关于x的函数解析式,并写出该函数的定义域;(2)、联结 ,当 时,求x的值;(3)、如果射线 与圆P的另一个公共点为点F,当 为直角三角形时,求 的面积.