安徽省宣城市2021年中考数学一模试卷
试卷更新日期:2021-05-08 类型:中考模拟
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 已知不等式组 其解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、 3. 根据安徽省公布的十三五铁路建设规划,到2021年,全省铁路建设总投资4370亿元.其中4370亿用科学记数法表示为( )A、 B、 C、 D、4. 某企业今年3月份产值为 万元,4月份比3月份减少了 ,5月份比4月份增加了 ,则5月份的产值是( )A、 万元 B、 万元 C、 万元 D、 万元5. 如图所示, 是 的直径, 切 于点 ,线段 交 于点 ,连接 ,若 ,则 等于( ).
3. 根据安徽省公布的十三五铁路建设规划,到2021年,全省铁路建设总投资4370亿元.其中4370亿用科学记数法表示为( )A、 B、 C、 D、4. 某企业今年3月份产值为 万元,4月份比3月份减少了 ,5月份比4月份增加了 ,则5月份的产值是( )A、 万元 B、 万元 C、 万元 D、 万元5. 如图所示, 是 的直径, 切 于点 ,线段 交 于点 ,连接 ,若 ,则 等于( ). A、27° B、32° C、36° D、54°6. 某班体育委员统计了全班45名同学一周的体育锻炼时间(单位:小时),并绘制了如图所示的折线统计图,下列说法中错误的是( )
A、27° B、32° C、36° D、54°6. 某班体育委员统计了全班45名同学一周的体育锻炼时间(单位:小时),并绘制了如图所示的折线统计图,下列说法中错误的是( )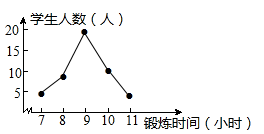 A、众数是9小时 B、中位数是9小时 C、平均数是9小时 D、锻炼时间不低于9小时的有14人7. 如图.在 中, , 垂直平分斜边 ,交 于 , 是垂足,连接 ,若 ,则 的长是( )
A、众数是9小时 B、中位数是9小时 C、平均数是9小时 D、锻炼时间不低于9小时的有14人7. 如图.在 中, , 垂直平分斜边 ,交 于 , 是垂足,连接 ,若 ,则 的长是( ) A、2 B、4 C、 D、8. 如图所示的二次函数 的图象中,某同学观察得出了下面四条信息:(1) ;(2) ;(3) ;(4) ;(5) 你认为其中错误的有( )
A、2 B、4 C、 D、8. 如图所示的二次函数 的图象中,某同学观察得出了下面四条信息:(1) ;(2) ;(3) ;(4) ;(5) 你认为其中错误的有( ) A、0个 B、1个 C、2个 D、3个9. ,则 =( )A、4 B、2 C、4或-2 D、4或210. 如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
A、0个 B、1个 C、2个 D、3个9. ,则 =( )A、4 B、2 C、4或-2 D、4或210. 如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )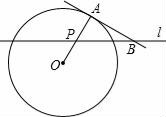 A、
A、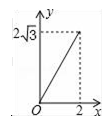 B、
B、 C、
C、 D、
D、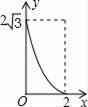
二、填空题
-
11. 分解因式: .12. 如图,在△ABC中,DE AB,CD:DA=2:3,DE=4,则AB的长为 .
 13. 如图,已知 内接于 , 为 的直径, ,弦 平分 ,若 ,则 .
13. 如图,已知 内接于 , 为 的直径, ,弦 平分 ,若 ,则 . 14. 我国南宋数学家杨辉所著的《详解九章算术》书中辑录了一个三角形数表,称之为“开方作法本源”图,即是著名的“杨辉三角形”.以下数表的构造思路源于“杨辉三角形”:
14. 我国南宋数学家杨辉所著的《详解九章算术》书中辑录了一个三角形数表,称之为“开方作法本源”图,即是著名的“杨辉三角形”.以下数表的构造思路源于“杨辉三角形”:
该表由若干行数字组成,从第二行起,每一行中的数字均等于“其肩上”两数之和,表中最后一行仅有一个数,则这个数为 .
三、解答题
-
15.16. 我国明代数学家程大位的名著《直接算法统亲》里有一道著名算题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?“意思是:有100个和尚分100个馒头,正好分完:如果大和尚一人分3个,小和尚3人分一个,试问大、小和尚各几人?17. 如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出 和 ;
 (1)、先作 关于直线1成轴对称的图形,再向上平移1个单位,得到 ;(2)、以图中的 为位似中心,将 作位似变换,且放大到原来的两倍,得到 ;并求出 的面积.18. 如图,佛山电视塔离小明家60米,小明从自家的阳台眺望电视塔,并测得塔尖 的仰角是 ,而塔底部 的俯角是 ,求佛山电视塔 的高度( 结果精确到1米)
(1)、先作 关于直线1成轴对称的图形,再向上平移1个单位,得到 ;(2)、以图中的 为位似中心,将 作位似变换,且放大到原来的两倍,得到 ;并求出 的面积.18. 如图,佛山电视塔离小明家60米,小明从自家的阳台眺望电视塔,并测得塔尖 的仰角是 ,而塔底部 的俯角是 ,求佛山电视塔 的高度( 结果精确到1米) 19. 如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE,CF相交于点D。
19. 如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE,CF相交于点D。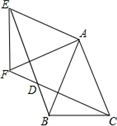 (1)、求证:BE=CF ;(2)、当四边形ACDE为菱形时,求BD的长。20. 孙明和王军两人去桃园游玩,返回时打算顺便买些新鲜油桃.此时桃园仅三箱油桃,价钱相同,但质量略有区别,分为 级、 级、 级,其中 级最好, 级最差.挑选时,三箱油桃不同时拿出,只能一箱一箱的看,也不告知该箱的质量等级.
(1)、求证:BE=CF ;(2)、当四边形ACDE为菱形时,求BD的长。20. 孙明和王军两人去桃园游玩,返回时打算顺便买些新鲜油桃.此时桃园仅三箱油桃,价钱相同,但质量略有区别,分为 级、 级、 级,其中 级最好, 级最差.挑选时,三箱油桃不同时拿出,只能一箱一箱的看,也不告知该箱的质量等级.两人采取了不同的选择方案:
孙明无论如何总是买第一次拿出来的那箱.
王军是先观察再确定,他不买第一箱油桃,而是仔细观察第一箱油桃的状况;如果第二箱油桃的质量比第一箱好,他就买第二箱油桃,如果第二箱的油桃不比第一箱好,他就买第三箱.
(1)、三箱油桃出现的先后顺序共有哪几种不同的可能?(2)、孙明与王军,谁买到 级的可能性大?为什么?21. 如图,在△ABC中,∠C=90°,AE平分∠BAC交BC于点E,O是AB上一点,经过A,E两点的⊙O交AB于点D,连接DE,作∠DEA的平分线EF交⊙O于点F,连接AF. (1)、求证:BC是⊙O的切线;(2)、若sin∠EFA= ,AF= ,求线段AC的长.22. 如图1,在 中, , , 于点 , 为 上一点,点 在 上,连接 并延长交 于点 ,且 .
(1)、求证:BC是⊙O的切线;(2)、若sin∠EFA= ,AF= ,求线段AC的长.22. 如图1,在 中, , , 于点 , 为 上一点,点 在 上,连接 并延长交 于点 ,且 . (1)、求证: ;(2)、求证: ;(3)、如图2,连接 ,若 , ,判断 是否为特殊三角形,并说明理由.23. 在平面直角坐标系中,直线 与x轴交于点B,与y轴交于点C,二次函数 的图象经过点B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.
(1)、求证: ;(2)、求证: ;(3)、如图2,连接 ,若 , ,判断 是否为特殊三角形,并说明理由.23. 在平面直角坐标系中,直线 与x轴交于点B,与y轴交于点C,二次函数 的图象经过点B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.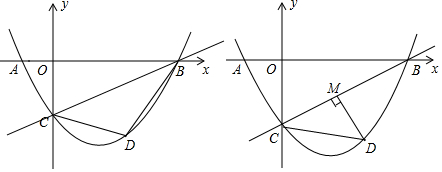 (1)、求二次函数的表达式;(2)、如图1,连接DC,DB,设△BCD的面积为S,求S的最大值;(3)、如图2,过点D作DM⊥BC于点M,是否存在点D,使得△CDM中的某个角恰好等于∠ABC的2倍?若存在,直接写出点D的横坐标;若不存在,请说明理由.
(1)、求二次函数的表达式;(2)、如图1,连接DC,DB,设△BCD的面积为S,求S的最大值;(3)、如图2,过点D作DM⊥BC于点M,是否存在点D,使得△CDM中的某个角恰好等于∠ABC的2倍?若存在,直接写出点D的横坐标;若不存在,请说明理由.