辽宁省抚顺市新抚区2021年中考数学一模试卷
试卷更新日期:2021-05-08 类型:中考模拟
一、单选题
-
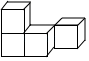
1. 在反比例函数 图象上的点是( )A、 B、 C、 D、2. 已知 为锐角,且 ,则 ( )A、 B、 C、 D、3. 如图是由4个大小相同的小正方体摆成的几何体,它的左视图是( )
 A、
A、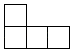 B、
B、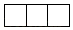 C、
C、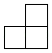 D、
D、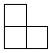 4. 一个由圆柱和长方体组成的几何体如图水平放置,它的俯视图是( )
4. 一个由圆柱和长方体组成的几何体如图水平放置,它的俯视图是( ) A、
A、 B、
B、 C、
C、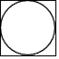 D、
D、 5. 在某一时刻,测得一根高为 的竹杆的影长为 ,同时测得一栋楼的影长为 ,则这栋楼的高度为( )A、 B、 C、 D、6. 如图,双曲线 经过 的对角线交点D,已知边 在y轴上,且 于点C,则 的面积是( )
5. 在某一时刻,测得一根高为 的竹杆的影长为 ,同时测得一栋楼的影长为 ,则这栋楼的高度为( )A、 B、 C、 D、6. 如图,双曲线 经过 的对角线交点D,已知边 在y轴上,且 于点C,则 的面积是( ) A、3 B、4 C、6 D、127. 如图,在 中, ,若 ,则 长为( )
A、3 B、4 C、6 D、127. 如图,在 中, ,若 ,则 长为( )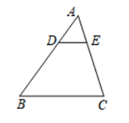 A、6 B、8 C、9 D、128. 如图,点A为反比例函数 图象上的一点,过点A作 轴于点B,点C为x轴上的一个动点, 的面积为3,则 k的值为( )
A、6 B、8 C、9 D、128. 如图,点A为反比例函数 图象上的一点,过点A作 轴于点B,点C为x轴上的一个动点, 的面积为3,则 k的值为( ) A、3 B、6 C、9 D、129. 把边长分别为1和2的两个正方形按图的方式放置.则图中阴影部分的面积为( )
A、3 B、6 C、9 D、129. 把边长分别为1和2的两个正方形按图的方式放置.则图中阴影部分的面积为( ) A、 B、 C、 D、10. 如图,菱形ABCD的边长为2,∠A=60°,一个以点B为顶点的60°角绕点B旋转,这个角的两边分别与线段AD的延长线及CD的延长线交于点P、Q,设DP=x,DQ=y,则能大致反映y与x的函数关系的图象是( )
A、 B、 C、 D、10. 如图,菱形ABCD的边长为2,∠A=60°,一个以点B为顶点的60°角绕点B旋转,这个角的两边分别与线段AD的延长线及CD的延长线交于点P、Q,设DP=x,DQ=y,则能大致反映y与x的函数关系的图象是( ) A、
A、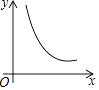 B、
B、 C、
C、 D、
D、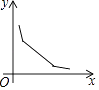
二、填空题
-
11. 计算: .12. 反比例函数 的图象经过点 ,则这个反比例函数的解析式是 .13. 若点 在反比例函数 的图象上,则代数式 的值为 .14. 一个圆锥的主视图是边长为6cm的正三角形,则这个圆锥的侧面积等于.15. 如图,在 中, 为 上一点,且 ,在 边上取一点E,使以 为顶点的三角形与 相似,则 等于 .
 16. 如图,在矩形 中, 为 边上一点,将 沿 翻折,点B落在点F处,当 为直角三角形时, .
16. 如图,在矩形 中, 为 边上一点,将 沿 翻折,点B落在点F处,当 为直角三角形时, . 17. 如图,矩形 的顶点 分别在 轴、 轴的正半轴上, 为 的中点,反比例函数 的图象经过点 ,且与 交于点 ,连接 , , ,若 的面积为3,则 的值为.
17. 如图,矩形 的顶点 分别在 轴、 轴的正半轴上, 为 的中点,反比例函数 的图象经过点 ,且与 交于点 ,连接 , , ,若 的面积为3,则 的值为. 18. 如图,在平面直角坐标系中,点 在 x轴上, 在直线 上,若 ,且 都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为 .则 可表示为 .
18. 如图,在平面直角坐标系中,点 在 x轴上, 在直线 上,若 ,且 都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为 .则 可表示为 .
三、解答题
-
19. 如图, 的三个顶点的坐标分别为 .
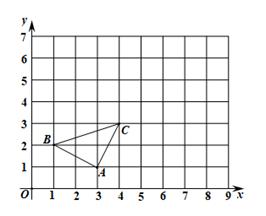 (1)、以原点O为位似中心,在第一象限内将 放大为原来的2倍得到 ,作出 ,写出 的坐标;(2)、P为第一象限的整点(横纵坐标都是整数的点), 平分 ,直接写出点P的坐标.20. 某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中选出一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
(1)、以原点O为位似中心,在第一象限内将 放大为原来的2倍得到 ,作出 ,写出 的坐标;(2)、P为第一象限的整点(横纵坐标都是整数的点), 平分 ,直接写出点P的坐标.20. 某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中选出一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.类别
A
B
C
D
E
类型
新闻
体育
动画
娱乐
戏曲
人数
11
20
40
m
4
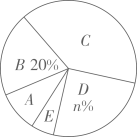
请你根据以上信息,回答下列问题:
(1)、统计表中m的值为 , 统计图中n的值为 , A类对应扇形的圆心角为度;(2)、该校共有1500名学生,根据调查结果,估计该校最喜爱体育节目的学生人数;(3)、样本数据中最喜爱戏曲节目的有4人,其中仅有1名男生.从这4人中任选2名同学去观赏戏曲表演,请用树状图或列表求所选2名同学中有男生的概率.21. 如图,点C的坐标为 ,点A在y轴正半轴上, ,且 .反比例函数 的图象经过点B. (1)、求点A的坐标;(2)、求反比例函数的解析式.22. 如图,在 中, ,以 为直径的⊙ 分别交 于点 ,点 在 的延长线上,且 .
(1)、求点A的坐标;(2)、求反比例函数的解析式.22. 如图,在 中, ,以 为直径的⊙ 分别交 于点 ,点 在 的延长线上,且 . (1)、求证: 是⊙ 的切线;(2)、若⊙ 的直径为3, ,求 和 的长.23. 图①是放置在水平面上的台灯,图②是其侧面示意图(台灯底座高度忽略不计),其中灯臂 ,灯罩 ,灯臂与底座构成的 . 可以绕点C上下调节一定的角度,当 时,点D到桌面的距离是多少?(精确到 ,参考数据: ).
(1)、求证: 是⊙ 的切线;(2)、若⊙ 的直径为3, ,求 和 的长.23. 图①是放置在水平面上的台灯,图②是其侧面示意图(台灯底座高度忽略不计),其中灯臂 ,灯罩 ,灯臂与底座构成的 . 可以绕点C上下调节一定的角度,当 时,点D到桌面的距离是多少?(精确到 ,参考数据: ). 24. “互联网 ”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售5条.设每条裤子的售价为x元(x为正整数),每月的销售量为y条.(1)、求y与x的函数关系式;(2)、设该网店每月获得的利润为w元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定每月从利润中捐出400元资助贫困学生.为了保证捐款后每月利润不低于4020元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?直接写出销售单价.
24. “互联网 ”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售5条.设每条裤子的售价为x元(x为正整数),每月的销售量为y条.(1)、求y与x的函数关系式;(2)、设该网店每月获得的利润为w元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定每月从利润中捐出400元资助贫困学生.为了保证捐款后每月利润不低于4020元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?直接写出销售单价.



