辽宁省抚顺市抚顺县2021年中考数学一模试卷
试卷更新日期:2021-05-08 类型:中考模拟
一、单选题
-
1. 下列函数中,y是x的反比例函数的是( )A、 B、 C、 D、2. 的值等于( )A、 B、 C、 D、3. 如图,从图甲到图乙的变换是( )
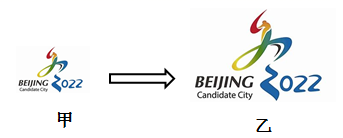 A、轴对称变换 B、平移变换 C、旋转变换 D、相似变换4. 下列现象是物体的投影的是( )A、小明看到镜子里的自己 B、灯光下猫咪映在墙上的影子 C、自行车行驶过后车轮留下的痕迹 D、掉在地上的树叶5. 矩形的长为x,宽为y,面积为9,则y与x之间的函数关系式用图象表示大致为( )A、
A、轴对称变换 B、平移变换 C、旋转变换 D、相似变换4. 下列现象是物体的投影的是( )A、小明看到镜子里的自己 B、灯光下猫咪映在墙上的影子 C、自行车行驶过后车轮留下的痕迹 D、掉在地上的树叶5. 矩形的长为x,宽为y,面积为9,则y与x之间的函数关系式用图象表示大致为( )A、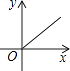 B、
B、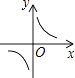 C、
C、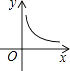 D、
D、 6. 如图1,放置的一个机器零件,若其主(正)视图如图2所示,则其俯视图为( )
6. 如图1,放置的一个机器零件,若其主(正)视图如图2所示,则其俯视图为( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 已知,AB是⊙O的直径,且C是圆上一点,小聪透过平举的放大镜从正上方看到水平桌面上的三角形图案的∠B(如图所示),那么下列关于∠A与放大镜中的∠B关系描述正确的是( )
7. 已知,AB是⊙O的直径,且C是圆上一点,小聪透过平举的放大镜从正上方看到水平桌面上的三角形图案的∠B(如图所示),那么下列关于∠A与放大镜中的∠B关系描述正确的是( ) A、∠A=∠B B、∠A+∠B=90° C、∠A+∠B>90° D、∠A+∠B的值无法确定8. 如图,在 中, 是斜边 上的高, ,则下列比值中等于 的是( )
A、∠A=∠B B、∠A+∠B=90° C、∠A+∠B>90° D、∠A+∠B的值无法确定8. 如图,在 中, 是斜边 上的高, ,则下列比值中等于 的是( ) A、 B、 C、 D、9. 如图,某高速公路建设中需要测量某条江的宽度 ,飞机上的测量人员在C处测得A、B两点的俯角分别为60°和45°.若飞机离地面的高度 为900m,且点H,A,B在同一水平直线上,则这条江的宽度 为( )
A、 B、 C、 D、9. 如图,某高速公路建设中需要测量某条江的宽度 ,飞机上的测量人员在C处测得A、B两点的俯角分别为60°和45°.若飞机离地面的高度 为900m,且点H,A,B在同一水平直线上,则这条江的宽度 为( ) A、 B、 C、 D、10. 如图,王华晚上由路灯A下的B处走到C处时,测得影子 的长为1m,继续往前走3m到达E处时,测得影子 的长为2m,已知王华的身高是1.5m,那么路灯A的高度 等于( )
A、 B、 C、 D、10. 如图,王华晚上由路灯A下的B处走到C处时,测得影子 的长为1m,继续往前走3m到达E处时,测得影子 的长为2m,已知王华的身高是1.5m,那么路灯A的高度 等于( )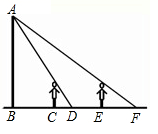 A、4.5m B、6m C、7.5m D、8m
A、4.5m B、6m C、7.5m D、8m二、填空题
-
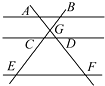
11. 如果反比例函数 的图象位于第二、第四象限内,则k .12. 如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,那么 的值等于 .
 13. 若点 , 都是反比例函数 图象上的点,并且 ,则 .(填“>”,“<”或“=”)14. 一幢4层楼房只有一个窗户亮着一盏灯,一棵小树和一根电线杆在窗口灯光下的影子如图所示,则亮着灯的窗口是号窗口.
13. 若点 , 都是反比例函数 图象上的点,并且 ,则 .(填“>”,“<”或“=”)14. 一幢4层楼房只有一个窗户亮着一盏灯,一棵小树和一根电线杆在窗口灯光下的影子如图所示,则亮着灯的窗口是号窗口.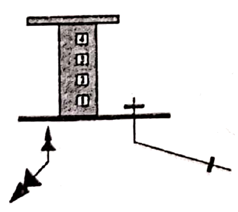 15. 如图,AB是⊙O的直径,点C和点D是⊙O上位于直径AB两侧的点,连接AC,AD,BD,CD,若⊙O的半径是5,BD=8,则cos∠ACD的值是 .
15. 如图,AB是⊙O的直径,点C和点D是⊙O上位于直径AB两侧的点,连接AC,AD,BD,CD,若⊙O的半径是5,BD=8,则cos∠ACD的值是 . 16. 如图,在正方形网格中有3个斜三角形:① ;② ;③ ;其中能与 相似的是 . ( 除外)
16. 如图,在正方形网格中有3个斜三角形:① ;② ;③ ;其中能与 相似的是 . ( 除外) 17. 某高铁路段修建过程中需要经过一座小山.如图,施工方计划沿 方向开挖隧道,为了加快施工速度,要在小山的另一侧D处(A、C、D共线)同时施工.测得 , , ,则 的长为 . (结果保留根号)
17. 某高铁路段修建过程中需要经过一座小山.如图,施工方计划沿 方向开挖隧道,为了加快施工速度,要在小山的另一侧D处(A、C、D共线)同时施工.测得 , , ,则 的长为 . (结果保留根号) 18. 如图,分别过x轴上点 , ,……, 作x轴的垂线,与反比例函数 ( )的图象的交点分别为 , ,……, ,若 的面积为 , 的面积为 ,……, 的面积为 ,则 . (用含n的式子表示)
18. 如图,分别过x轴上点 , ,……, 作x轴的垂线,与反比例函数 ( )的图象的交点分别为 , ,……, ,若 的面积为 , 的面积为 ,……, 的面积为 ,则 . (用含n的式子表示)
三、解答题
-
19. 先化简,再求值:
,其中 , .
20. 教师办公室有一台可以自动加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热.每分钟水温上升10℃,待加热到100℃时,饮水机自动停止加热,水温开始下降.在水温开始下降的过程中,水温y(℃)和通电时间x( )成反比例关系.直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温均为20℃,接通电源后,水温y(℃)和通电时间x( )之间的关系如图所示,回答下列问题: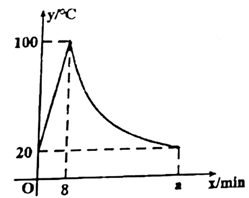 (1)、分别求出当 和 时,y和x之间的函数关系式;(2)、求出图中a的值;(3)、李老师这天7:30将饮水机电源打开,若他想在8:10上课前喝到不低于40℃的开水,则他需要在通电多长时间内接水?21. 如图, 在坐标平面内,三个顶点的坐标分别为 , , (正方形网格中,每个小正方形的边长均是1个单位长度).
(1)、分别求出当 和 时,y和x之间的函数关系式;(2)、求出图中a的值;(3)、李老师这天7:30将饮水机电源打开,若他想在8:10上课前喝到不低于40℃的开水,则他需要在通电多长时间内接水?21. 如图, 在坐标平面内,三个顶点的坐标分别为 , , (正方形网格中,每个小正方形的边长均是1个单位长度). (1)、 与 关于x轴成轴对称,请画出 ,并写出 点的坐标;(2)、以点 为位似中心,将 放大得到 ,放大前后的面积之比为 ,画出 ,使它与 在位似中心同侧,并写出 点的坐标;(3)、连接 、 ,判断 的形状并直接写出结论.22. 某工厂要加工一批上下底密封纸盒,设计者给出了密封纸盒的三视图,如图1.
(1)、 与 关于x轴成轴对称,请画出 ,并写出 点的坐标;(2)、以点 为位似中心,将 放大得到 ,放大前后的面积之比为 ,画出 ,使它与 在位似中心同侧,并写出 点的坐标;(3)、连接 、 ,判断 的形状并直接写出结论.22. 某工厂要加工一批上下底密封纸盒,设计者给出了密封纸盒的三视图,如图1. (1)、由三视图可知,密封纸盒的形状是;(2)、根据该几何体的三视图,在图2中补全它的表面展开图;(3)、请你根据图1中数据,计算这个密封纸盒的表面积.(结果保留根号)23. 在数学综合实践活动上,某小组要测量学校升旗台旗杆的高度.如图所示,测得 ,斜坡 的长为6m,坡度 是指坡面的铅直高度 与水平宽度 的比,在点B处测得旗杆顶端的仰角为70°,点B到旗杆底部C的距离为4m.
(1)、由三视图可知,密封纸盒的形状是;(2)、根据该几何体的三视图,在图2中补全它的表面展开图;(3)、请你根据图1中数据,计算这个密封纸盒的表面积.(结果保留根号)23. 在数学综合实践活动上,某小组要测量学校升旗台旗杆的高度.如图所示,测得 ,斜坡 的长为6m,坡度 是指坡面的铅直高度 与水平宽度 的比,在点B处测得旗杆顶端的仰角为70°,点B到旗杆底部C的距离为4m. (1)、求斜坡 的坡角 的度数;(2)、求旗杆顶端离地面的高度 .
(1)、求斜坡 的坡角 的度数;(2)、求旗杆顶端离地面的高度 .(参考数据: , , ,结果精确到1m)
24. 如图1,已知双曲线 ( )与直线 交于A、B两点,点A的坐标为 ,回答下列问题: (1)、点B的坐标为;当x满足时, ;(2)、如图2,过原点O作另一条直线,交双曲线 ( )于P、Q两点,点P在第一象限,
(1)、点B的坐标为;当x满足时, ;(2)、如图2,过原点O作另一条直线,交双曲线 ( )于P、Q两点,点P在第一象限,①若点P的横坐标为1,求 的面积;
②四边形 一定是什么图形;
③四边形 可能是正方形吗?若可能,请直接写出你的结论;若不可能,请说明理由.
25. 在矩形 中, ,点E是直线 上的一点,点F是直线 上的一点,且满足 ,连接 交 于点G. (1)、 ;(2)、如图1,当点E在 上,点F在线段 的延长线上时,
(1)、 ;(2)、如图1,当点E在 上,点F在线段 的延长线上时,①求证: ;
②求证: ;
(3)、如图2,当点E在 的延长线上,点F在线段 上时, 与 相交于点H,① 这个结论是否仍然成立?请直接写出你的结论:
②当 , 时,请直接写出 的长.
26. 如图1,抛物线 与x轴交于点 、点 ,与y轴交于点C,抛物线的对称轴与x轴交于点F. (1)、抛物线的解析式为:;直线 的解析式为:;(2)、若点P为抛物线位于第四象限图象上的一个动点,设 的面积为S,求S最大时点P的坐标及S的最大值;(3)、在(2)的条件下,过点P作 轴于点E,交直线 于点D,在x轴上是否存在点M,使得以B、D、M为顶点的三角形与 相似?若存在,请直接写出点M的坐标;若不存在,请说明理由.
(1)、抛物线的解析式为:;直线 的解析式为:;(2)、若点P为抛物线位于第四象限图象上的一个动点,设 的面积为S,求S最大时点P的坐标及S的最大值;(3)、在(2)的条件下,过点P作 轴于点E,交直线 于点D,在x轴上是否存在点M,使得以B、D、M为顶点的三角形与 相似?若存在,请直接写出点M的坐标;若不存在,请说明理由.