辽宁省鞍山市铁西区2021年中考数学3月模拟试卷
试卷更新日期:2021-05-08 类型:中考模拟
一、单选题
-
1.
如图放置的几何体的左视图是( )
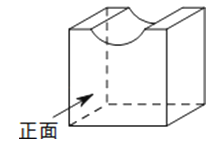 A、
A、 B、
B、 C、
C、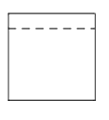 D、
D、 2. 纳米是非常小的长度单位,已知1纳米= 毫米,某种病毒的直径为100纳米,若将这种病毒排成1毫米长,则病毒的个数是( )A、102 个 B、104 个 C、105个 D、108个3. 如图,直线l1//l2 , 点A在直线l1上,以点A为圆心,适当长为半径画弧,分别交直线l1、l2于B,C两点,连结AC,BC.若∠ABC=54°,则∠1的大小为( )
2. 纳米是非常小的长度单位,已知1纳米= 毫米,某种病毒的直径为100纳米,若将这种病毒排成1毫米长,则病毒的个数是( )A、102 个 B、104 个 C、105个 D、108个3. 如图,直线l1//l2 , 点A在直线l1上,以点A为圆心,适当长为半径画弧,分别交直线l1、l2于B,C两点,连结AC,BC.若∠ABC=54°,则∠1的大小为( ) A、36° B、54° C、72° D、73°4. 下列运算正确的是( )A、 B、 C、 D、5. 如图, 是 的外接圆,半径为 ,若 ,则 的度数为( )
A、36° B、54° C、72° D、73°4. 下列运算正确的是( )A、 B、 C、 D、5. 如图, 是 的外接圆,半径为 ,若 ,则 的度数为( )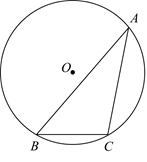 A、30° B、25° C、15° D、10°6. 在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:
A、30° B、25° C、15° D、10°6. 在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:成绩/m
1.50
1.60
1.65
1.70
1.75
1.80
人数
2
3
2
3
4
1
则这些运动员成绩的中位数、众数分别为( )
A、1.65、1.70 B、1.65、1.75 C、1.70、1.75 D、1.70、1.707. 如图,在△ABC中,AB= ,AC= ,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1 , 连接BC1 , 则BC1的长为( ) A、3 B、2 C、2 D、48. 如图, 中, , , ,点P是斜边AB上任意一点,过点P作 ,垂足为P,交边 或边 于点Q,设 , 的面积为y,则y与x之间的函数图象大致是
A、3 B、2 C、2 D、48. 如图, 中, , , ,点P是斜边AB上任意一点,过点P作 ,垂足为P,交边 或边 于点Q,设 , 的面积为y,则y与x之间的函数图象大致是 A、
A、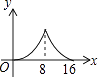 B、
B、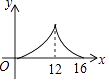 C、
C、 D、
D、
二、填空题
-
9. 分解因式:10. 关于x的一元二次方程 有两个不相等的实数根,则m的范围11. 如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是 .
 12. 一个有进水管和出水管的容器,从某时刻开始4 min内只进水不出水,在随后的8 min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则每分钟的出水量为
12. 一个有进水管和出水管的容器,从某时刻开始4 min内只进水不出水,在随后的8 min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则每分钟的出水量为 13. 如图,等腰Rt△ABP的斜边AB=2,点M、N在斜边AB上.若△PMN是等腰三角形且底角正切值为2,则MN= .
13. 如图,等腰Rt△ABP的斜边AB=2,点M、N在斜边AB上.若△PMN是等腰三角形且底角正切值为2,则MN= . 14. 如图,O是坐标原点,菱形OABC的顶点A的坐标为(﹣3,4),顶点C在x轴的负半轴上,函数y= (x<0)的图象经过顶点B,则k的值为 .
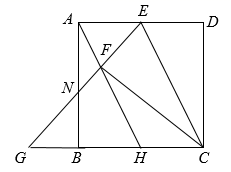
14. 如图,O是坐标原点,菱形OABC的顶点A的坐标为(﹣3,4),顶点C在x轴的负半轴上,函数y= (x<0)的图象经过顶点B,则k的值为 .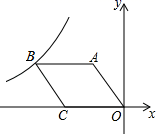 15. 如图,在正方形 中, 为 边中点,连接 ,将 沿 翻折,得到 ,延长 分别交 、 延长线于 、 两点,连接 ,延长 交 边于点 ,则下列正确的有
15. 如图,在正方形 中, 为 边中点,连接 ,将 沿 翻折,得到 ,延长 分别交 、 延长线于 、 两点,连接 ,延长 交 边于点 ,则下列正确的有①四边形 为平行四边形;② ,③ ,④ ;
 16. 如图,等边三角形 的边长为2,顶点 与原点 重合,点 在 轴的正半轴上,过点 作 于点 ,过点 作 ,交 于点 ;过点 作 于点 ,过点 作 ,交 于点 ;……,按此规律进行下去,点 的坐标是
16. 如图,等边三角形 的边长为2,顶点 与原点 重合,点 在 轴的正半轴上,过点 作 于点 ,过点 作 ,交 于点 ;过点 作 于点 ,过点 作 ,交 于点 ;……,按此规律进行下去,点 的坐标是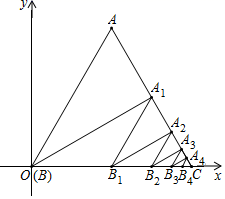
三、解答题
-
17. 先化简( -x+1)÷ ,再从-1,0,1中选择合适的x值代入求值.18. 如图, 的三个顶点坐标分别为 , , .
 (1)、画出 关于 轴对称的 ;(2)、以点 为位似中心,在如图所示的网格中画出 的位似图形 ,使 与 的相似比为2:1;(3)、画出 绕点 逆时针旋转 的 ,并写出线段 扫过的面积19. 某学校为了丰富学生课余生活,开展了“第二课堂”活动,推出了以下四种选修课程: .绘画; .唱歌; .跳舞; .演讲; .书法.学校规定:每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.
(1)、画出 关于 轴对称的 ;(2)、以点 为位似中心,在如图所示的网格中画出 的位似图形 ,使 与 的相似比为2:1;(3)、画出 绕点 逆时针旋转 的 ,并写出线段 扫过的面积19. 某学校为了丰富学生课余生活,开展了“第二课堂”活动,推出了以下四种选修课程: .绘画; .唱歌; .跳舞; .演讲; .书法.学校规定:每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.
请结合统计图中的信息解决下列问题:
(1)、这次抽查的学生人数是多少人?(2)、将条形统计图补充完整.(3)、求扇形统计图中课程 所对应扇形的圆心角的度数.(4)、如果该校共有1200名学生,请你估计该校选择课程 的学生约有多少人.20. 疫情防控期间,任何人进入校园都必须测量体温,体温正常方可进校.甲、乙两位同学进校时可以从学校大门A、B、C三个入口处中的任意一处测量体温.(1)、甲同学在A入口处测量体温的概率是 ;(2)、求甲、乙两位同学在同一入口处测量体温的概率.(用“画树状图”或“列表”的方法写出分析过程)21. 如图,小岛 在港口 的南偏西 方向,距离港口81海里处,甲船从 出发,沿 方向以9海里/时的速度驶向港口,乙船从港口 出发,沿南偏东 方向,以18海里/时的速度驶离港口,现两船同时出发,( , , ) (1)、出发后几小时两船与港口 的距离相等?(2)、出发后几小时乙船在甲船的正东方向?22. 如图,直线y1=﹣x+4,y2= x+b都与双曲线y= 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)、出发后几小时两船与港口 的距离相等?(2)、出发后几小时乙船在甲船的正东方向?22. 如图,直线y1=﹣x+4,y2= x+b都与双曲线y= 交于点A(1,m),这两条直线分别与x轴交于B,C两点.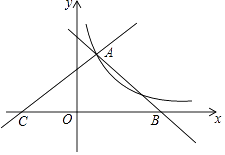 (1)、求y与x之间的函数关系式;
(1)、求y与x之间的函数关系式;
(2)、直接写出当x>0时,不等式 x+b> 的解集;(3)、若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.23. 如图,M,N是以AB为直径的⊙O上的点,且 = ,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F. (1)、求证:MF是⊙O的切线;(2)、若CN=3,BN=4,求CM的长.24. 某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.(1)、求y与x之间的函数关系式;(2)、当每件售价定为多少元时,每星期的销售利润最大,最大利润是多少元?(3)、若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?25.(1)、证明推断:如图(1),在正方形 中,点 , 分别在边 , 上, 于点 ,点 , 分别在边 , 上, .求证: ;
(1)、求证:MF是⊙O的切线;(2)、若CN=3,BN=4,求CM的长.24. 某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.(1)、求y与x之间的函数关系式;(2)、当每件售价定为多少元时,每星期的销售利润最大,最大利润是多少元?(3)、若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?25.(1)、证明推断:如图(1),在正方形 中,点 , 分别在边 , 上, 于点 ,点 , 分别在边 , 上, .求证: ; (2)、类比探究:如图(2),在矩形 中, 将矩形 沿 折叠,使点 落在 边上的点 处,得到四边形 , 交 于点 ,连接 交 于点 .试探究 与 之间的数量关系,并说明理由;
(2)、类比探究:如图(2),在矩形 中, 将矩形 沿 折叠,使点 落在 边上的点 处,得到四边形 , 交 于点 ,连接 交 于点 .试探究 与 之间的数量关系,并说明理由;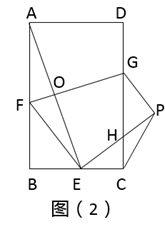 (3)、拓展应用:在(2)的条件下,连接 ,若 , ,求 的长.26. 如图(1)在平面直角坐标系中,抛物线 ( )交 轴于点 , 与 轴交于点 ,连接 ,连接 ,点 是抛物线一点且位于直线 上方,作 平行于 轴交 于点
(3)、拓展应用:在(2)的条件下,连接 ,若 , ,求 的长.26. 如图(1)在平面直角坐标系中,抛物线 ( )交 轴于点 , 与 轴交于点 ,连接 ,连接 ,点 是抛物线一点且位于直线 上方,作 平行于 轴交 于点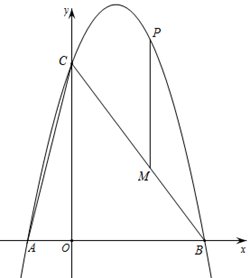 (1)、求抛物线解析式并直接写出直线 解析式(2)、求 的最大值及点 坐标(3)、在抛物线对称轴上是否存在点 ,使 ,若存在请直接写出点 坐标;若不存在请说出理由
(1)、求抛物线解析式并直接写出直线 解析式(2)、求 的最大值及点 坐标(3)、在抛物线对称轴上是否存在点 ,使 ,若存在请直接写出点 坐标;若不存在请说出理由