辽宁省鞍山市铁东区2021年中考数学一模试卷
试卷更新日期:2021-05-08 类型:中考模拟
一、单选题
-
1. 的值是( )A、2020 B、-2020 C、 D、2. 一个几何体的三视图如图所示,则这个几何体是( )
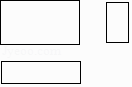 A、圆锥 B、长方体 C、圆柱 D、球3. 习近平总书记提出了未来五年“精准扶贫”的战略构想,意味着每年要减贫约11700000人,将数据11700000用科学记数法表示为( )A、1.17×107 B、11.7×106 C、0.117×107 D、1.17×1084. 如图, ,点E在CD上,点F在AB上,如果 , ,那么 的度数为( )
A、圆锥 B、长方体 C、圆柱 D、球3. 习近平总书记提出了未来五年“精准扶贫”的战略构想,意味着每年要减贫约11700000人,将数据11700000用科学记数法表示为( )A、1.17×107 B、11.7×106 C、0.117×107 D、1.17×1084. 如图, ,点E在CD上,点F在AB上,如果 , ,那么 的度数为( ) A、 B、 C、 D、5. 下列运算中正确的是( )A、 B、 C、 D、6. 如图,在 中,弦AB垂直平分半径OC,OC=2,则弦AB的长为( )
A、 B、 C、 D、5. 下列运算中正确的是( )A、 B、 C、 D、6. 如图,在 中,弦AB垂直平分半径OC,OC=2,则弦AB的长为( )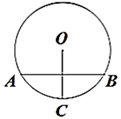 A、 B、 C、 D、7. 如图,点 在反比例函数 上,点 在反比例函数 上, , 轴,则k的值为( )
A、 B、 C、 D、7. 如图,点 在反比例函数 上,点 在反比例函数 上, , 轴,则k的值为( )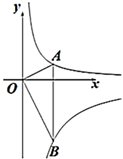 A、-16 B、-8 C、-6 D、-48. 如图,F为正方形ABCD的边CD上一动点,AB=2,连接BF,过A作AH⊥BF
A、-16 B、-8 C、-6 D、-48. 如图,F为正方形ABCD的边CD上一动点,AB=2,连接BF,过A作AH⊥BF交BC于H,交BF于G,连接CG,当CG为最小值时,CH的长为( )
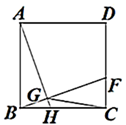 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
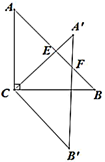
9. 已知圆锥的底面半径是2cm,母线长是3cm,则圆锥侧面积是.10. 分解因式:11. 如图,在等腰直角三角形ABC中, , ,把 绕点C顺时针旋转 得到 ,边 、 分别交AB于E、F,则 的长为.
 12. 在函数y=中,自变量x的取值范围是 .
12. 在函数y=中,自变量x的取值范围是 .
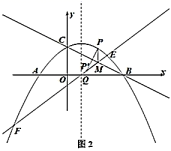
13. 如图,在平面直角坐标系第一象限中,线段AB、CD是以原点O为位似中心的位似图形,且相似比为 , 轴,点A、点C在x轴上, ,则B点坐标为.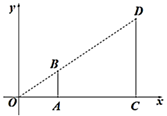 14. 现代互联网技术的广泛应用,催生了快递行业的高速发展.据调查,某家小型快递公司的分拣工小李和小江,在分拣同一类物件时,小李分拣120个物件所用的时间与小江分拣90个物件所用的时间相同,已知小李每小时比小江多分拣20个物件.若设小江每小时分拣 个物件,则可列方程方程为.15. 如图, 、 切 于 、 两点,连接 交 于点 ,交弧 于点 , ,点 为优弧 上一点, ,则 的大小为 .
14. 现代互联网技术的广泛应用,催生了快递行业的高速发展.据调查,某家小型快递公司的分拣工小李和小江,在分拣同一类物件时,小李分拣120个物件所用的时间与小江分拣90个物件所用的时间相同,已知小李每小时比小江多分拣20个物件.若设小江每小时分拣 个物件,则可列方程方程为.15. 如图, 、 切 于 、 两点,连接 交 于点 ,交弧 于点 , ,点 为优弧 上一点, ,则 的大小为 . 16. 已知二次函数 ( )图象的对称轴为直线 ,部分图象如图所示,下列结论中:① ;② ;③ ;④若 为任意实数,则有 ;⑤当图象经过点 时,方程 的两根为 , ,则 ,其中正确的结论有 .
16. 已知二次函数 ( )图象的对称轴为直线 ,部分图象如图所示,下列结论中:① ;② ;③ ;④若 为任意实数,则有 ;⑤当图象经过点 时,方程 的两根为 , ,则 ,其中正确的结论有 .
三、解答题
-
17. 先化简,再求值: ,其中 的值从不等式组 的整数解中选取.18. 在平面直角坐标系中, 的位置如图所示:(每个方格都是边长为1个单位长度的正方形, 的顶点都在格点上).
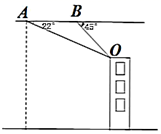
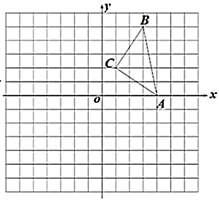 (1)、画出 关于 轴对称的 ;写出 点对应点 的坐标;(2)、将 绕点 逆时针旋转 得到 ,请你求出线段 旋转过程中扫过的面积.19. 对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.(1)、甲组抽到A小区的概率是多少(2)、请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.20. 近年来,无人机航拍测量的应用越来越广泛.如图无人机从 处观测,测得某建筑物顶点 的俯角为 ,继续水平前行10米到达 处,测得俯角为 ,已知无人机的飞行高度为45米,则这栋楼的高度是多少米?(精确到0.1米)
(1)、画出 关于 轴对称的 ;写出 点对应点 的坐标;(2)、将 绕点 逆时针旋转 得到 ,请你求出线段 旋转过程中扫过的面积.19. 对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.(1)、甲组抽到A小区的概率是多少(2)、请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.20. 近年来,无人机航拍测量的应用越来越广泛.如图无人机从 处观测,测得某建筑物顶点 的俯角为 ,继续水平前行10米到达 处,测得俯角为 ,已知无人机的飞行高度为45米,则这栋楼的高度是多少米?(精确到0.1米)参考数据: , , .
 21. 在如图菱形 中,点 是 边上一点,连接 ,点 是 上的两点,连接 , ,使得 , .
21. 在如图菱形 中,点 是 边上一点,连接 ,点 是 上的两点,连接 , ,使得 , .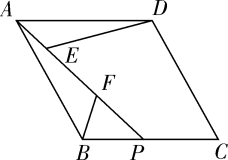 (1)、求证: ;(2)、求证: .22. 如图,直线 与反比例函数 ( )的图象交于点 与x轴交于点 ,M为该图象上任意一点,过M点作x轴的平行线交y轴于点P,交AB于点N.
(1)、求证: ;(2)、求证: .22. 如图,直线 与反比例函数 ( )的图象交于点 与x轴交于点 ,M为该图象上任意一点,过M点作x轴的平行线交y轴于点P,交AB于点N. (1)、求m、n的值和反比例函数的表达式;(2)、若点 为 中点时,求 的面积.23. 如图,AB为⊙O直径,AC为弦,过⊙O外的点D作DE⊥OA于点E,交AC于点F,连接DC并延长交AB的延长线于点H,且∠D=2∠A.
(1)、求m、n的值和反比例函数的表达式;(2)、若点 为 中点时,求 的面积.23. 如图,AB为⊙O直径,AC为弦,过⊙O外的点D作DE⊥OA于点E,交AC于点F,连接DC并延长交AB的延长线于点H,且∠D=2∠A.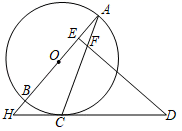 (1)、求证:DC与⊙O相切;(2)、若⊙O半径为4, ,求AC的长.24. 某企业接到一批防护服生产任务,按要求15天完成,已知这批防护服的出厂价为每件80元,为按时完成任务,该企业动员放假回家的工人及时返回加班赶制.该企业第x天生产的防护服数量为y件,y与x之间的关系可以用图中的函数图象来刻画.
(1)、求证:DC与⊙O相切;(2)、若⊙O半径为4, ,求AC的长.24. 某企业接到一批防护服生产任务,按要求15天完成,已知这批防护服的出厂价为每件80元,为按时完成任务,该企业动员放假回家的工人及时返回加班赶制.该企业第x天生产的防护服数量为y件,y与x之间的关系可以用图中的函数图象来刻画.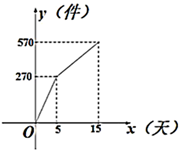 (1)、直接写出y与x的函数关系式;(2)、由于疫情加重,原材料紧缺,防护服的成本前5天为每件50元,从第6天起每件防护服的成本比前一天增加2元,设第x天创造的利润为w元,直接利用(1)的结论,求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)25. 已知 和 中, , , (其中 ),连接AD、CE,点M为线段AD的中点,连接ME、MC, 绕点B顺时针旋转,探究线段ME与MC的数量关系.
(1)、直接写出y与x的函数关系式;(2)、由于疫情加重,原材料紧缺,防护服的成本前5天为每件50元,从第6天起每件防护服的成本比前一天增加2元,设第x天创造的利润为w元,直接利用(1)的结论,求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)25. 已知 和 中, , , (其中 ),连接AD、CE,点M为线段AD的中点,连接ME、MC, 绕点B顺时针旋转,探究线段ME与MC的数量关系.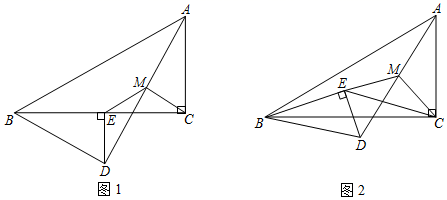
 (1)、如图1,点E落在BC边上时,探究ME与MC的数量关系,并说明理由;(2)、如图2,点E落在 内部时,探究ME与MC的数量关系,并说明理由;(3)、若 , ,当A、E、D共线时,直接写出 的值.26. 如图,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交点 ,抛物线 经过 , 两点,与 轴交于另一点 .如图1,点 为抛物线上任意一点,过点 作 轴交 于 .
(1)、如图1,点E落在BC边上时,探究ME与MC的数量关系,并说明理由;(2)、如图2,点E落在 内部时,探究ME与MC的数量关系,并说明理由;(3)、若 , ,当A、E、D共线时,直接写出 的值.26. 如图,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交点 ,抛物线 经过 , 两点,与 轴交于另一点 .如图1,点 为抛物线上任意一点,过点 作 轴交 于 . (1)、求抛物线的解析式;(2)、当 是直角三角形时,求 点坐标;(3)、如图2,作
(1)、求抛物线的解析式;(2)、当 是直角三角形时,求 点坐标;(3)、如图2,作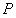 点关于直线
点关于直线 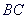 的对称点
的对称点 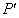 ,作直线
,作直线  与抛物线交于
与抛物线交于  ,设抛物线对称轴与
,设抛物线对称轴与 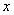 轴交点为
轴交点为 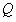 ,当直线
,当直线  经过点
经过点 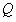 时,请你直接写出
时,请你直接写出  的长.
的长.