黑龙江省哈尔滨市南岗区2021年中考数学模拟试卷
试卷更新日期:2021-05-08 类型:中考模拟
一、单选题
-
1. ﹣ 的相反数是( )A、﹣5 B、5 C、﹣ D、2. 下列运算正确的是( ).A、3a2﹣a2=3 B、(a+b)2=a2+b2 C、(﹣3ab2 )2=6a2b4 D、a2•a4=a63. 下列四个图形中,中心对称图形是( )A、
 B、
B、 C、
C、
D、
D、 4. 下面四个几何体中,主视图为三角形的是( )A、
4. 下面四个几何体中,主视图为三角形的是( )A、 B、
B、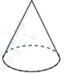 C、
C、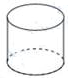 D、
D、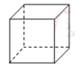 5. 不等式组 的解集是( )A、 B、 C、 D、6. 一个不透明的袋子里装有4个红球和2个黄球,它们除颜色外其余都相同.从袋中任意摸出一个球是红球的概率为( )A、 B、 C、 D、7. 如图,在 中, ,将 绕点A按逆时针方向旋转得到 .若点 恰好落在 边上,且 ,则 的度数为( )
5. 不等式组 的解集是( )A、 B、 C、 D、6. 一个不透明的袋子里装有4个红球和2个黄球,它们除颜色外其余都相同.从袋中任意摸出一个球是红球的概率为( )A、 B、 C、 D、7. 如图,在 中, ,将 绕点A按逆时针方向旋转得到 .若点 恰好落在 边上,且 ,则 的度数为( )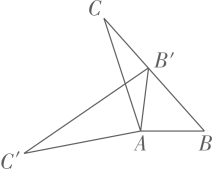 A、 B、 C、 D、8. 通过平移抛物线y=(x﹣2)2+7,可得到抛物线y=x2 , 下列平移方法正确的是( ).A、向左平移2个单位长度,再向上平移7个单位长度 B、向左平移2个单位长度,再向下平移7个单位长度 C、向右平移2个单位长度,再向上平移7个单位长度 D、向右平移2个单位长度,再向下平移7个单位长度9. 往直径为 的圆柱形容器内装入一些水以后,截面如图所示,若水面宽 ,则水的最大深度为( )
A、 B、 C、 D、8. 通过平移抛物线y=(x﹣2)2+7,可得到抛物线y=x2 , 下列平移方法正确的是( ).A、向左平移2个单位长度,再向上平移7个单位长度 B、向左平移2个单位长度,再向下平移7个单位长度 C、向右平移2个单位长度,再向上平移7个单位长度 D、向右平移2个单位长度,再向下平移7个单位长度9. 往直径为 的圆柱形容器内装入一些水以后,截面如图所示,若水面宽 ,则水的最大深度为( )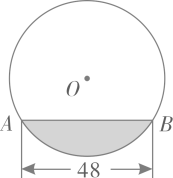 A、 B、 C、 D、10. 如图,AC是▱ABCD的对角线,点E是AB的延长线上的一点,连接DE,分别交BC,AC于点F,G,则下列式子一定正确的是( ).
A、 B、 C、 D、10. 如图,AC是▱ABCD的对角线,点E是AB的延长线上的一点,连接DE,分别交BC,AC于点F,G,则下列式子一定正确的是( ).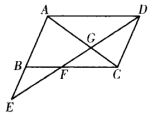 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 近年来,华为手机越来越受到消费者的青睐,截止2019年12月底,华为5G手机全球总发货量突破6 900 000台,将6 900 000用科学记数法表示为 .12. 函数 中,自变量x的取值范围是 .13. 计算 的结果为 .14. 把多项式xy2﹣9x分解因式的结果是 .15. 抛物线y=﹣5x2+10x﹣1的对称轴为直线x= .16. 方程组 的解为 .17. 如图,若反比例函数y= (x<0)的图象经过点A , AB⊥x轴于B , 且△AOB的面积为6,则k= .
 18. 一个扇形的圆心角是 ,半径为4,则这个扇形的面积为 . (结果保留 )19. 在正方形ABCD中,AB=8,点P是正方形边上一点,若PD=3AP,则AP的长为 .20. 如图,在平行四边形ABCD中,AD=5,AB=2 ,∠B是锐角,AE⊥BC于点E,F是AB的中点,连接DF,EF,若∠EFD=90°,则AE的长为 .
18. 一个扇形的圆心角是 ,半径为4,则这个扇形的面积为 . (结果保留 )19. 在正方形ABCD中,AB=8,点P是正方形边上一点,若PD=3AP,则AP的长为 .20. 如图,在平行四边形ABCD中,AD=5,AB=2 ,∠B是锐角,AE⊥BC于点E,F是AB的中点,连接DF,EF,若∠EFD=90°,则AE的长为 .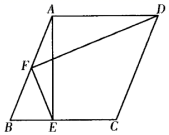
三、解答题
-
21. 先化简,再求代数式(1﹣ )÷ 的值,其中x=2cos45°+1.22. 如图,在6×4的方格纸ABCD中,请按要求画格点线段(端点在格点上),且线段的端点均不与点A,B,C,D重合.
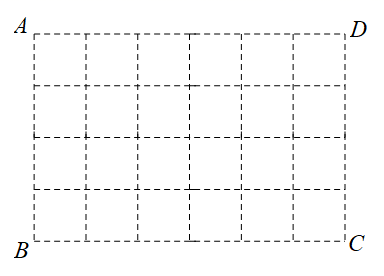 (1)、在图1中画格点线段EF,GH各一条,使点E,F,G,H分别落在边AB,BC,CD,DA上,且EF=GH,EF不平行GH;(2)、在图2中画格点线段MN,PQ各一条,使点M,N,P,Q分别落在边AB,BC,CD,DA上,且PQ= MN.23. 新学期,某校开设了“防疫宣传”“心理疏导”等课程.为了解学生对新开设课程的掌握情况,从九年级学生中随机抽取了部分学生进行了一次综合测试.测试结果分为四个等级:A级为优秀,B级为良好,C级为及格,D级为不及格.将测试结果绘制了如图两幅不完整的统计图.根据统计图中的信息解答下列问题:
(1)、在图1中画格点线段EF,GH各一条,使点E,F,G,H分别落在边AB,BC,CD,DA上,且EF=GH,EF不平行GH;(2)、在图2中画格点线段MN,PQ各一条,使点M,N,P,Q分别落在边AB,BC,CD,DA上,且PQ= MN.23. 新学期,某校开设了“防疫宣传”“心理疏导”等课程.为了解学生对新开设课程的掌握情况,从九年级学生中随机抽取了部分学生进行了一次综合测试.测试结果分为四个等级:A级为优秀,B级为良好,C级为及格,D级为不及格.将测试结果绘制了如图两幅不完整的统计图.根据统计图中的信息解答下列问题: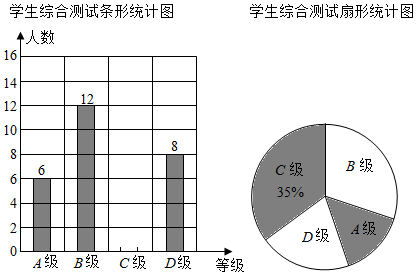 (1)、本次抽样测试的学生是多少人?(2)、通过计算把条形统计图补充完整;(3)、该校九年级共有学生600名,如果全部参加这次测试,估计优秀的学生是多少人?24. 已知:在△ABC和△DBE中,AB=DB,BC=BE,其中∠ABD=∠CBE.
(1)、本次抽样测试的学生是多少人?(2)、通过计算把条形统计图补充完整;(3)、该校九年级共有学生600名,如果全部参加这次测试,估计优秀的学生是多少人?24. 已知:在△ABC和△DBE中,AB=DB,BC=BE,其中∠ABD=∠CBE.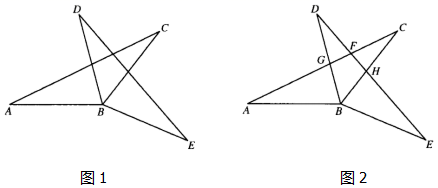 (1)、如图1,求证:AC=DE;(2)、如图2,AB=BC,AC分别交DE,BD于点F,G,BC交DE于点H,在不添加任何辅助线的情况下,请直接写出图2中的四对全等三角形.25. 某地有甲、乙两家口罩厂,已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且乙厂单独完成48万只口罩的生产比甲厂单独完成48万只口罩的生产多用4天.(1)、求甲、乙厂每天分别可以生产多少万只口罩?(2)、该地委托甲、乙两厂尽快完成100万只口罩的生产任务,问两厂同时生产至少需要多少天才能完成生产任务?26. 已知:AB,CD都是⊙O的直径,点E为 上一点,连接BE,CE,且∠BEC=45°.
(1)、如图1,求证:AC=DE;(2)、如图2,AB=BC,AC分别交DE,BD于点F,G,BC交DE于点H,在不添加任何辅助线的情况下,请直接写出图2中的四对全等三角形.25. 某地有甲、乙两家口罩厂,已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且乙厂单独完成48万只口罩的生产比甲厂单独完成48万只口罩的生产多用4天.(1)、求甲、乙厂每天分别可以生产多少万只口罩?(2)、该地委托甲、乙两厂尽快完成100万只口罩的生产任务,问两厂同时生产至少需要多少天才能完成生产任务?26. 已知:AB,CD都是⊙O的直径,点E为 上一点,连接BE,CE,且∠BEC=45°.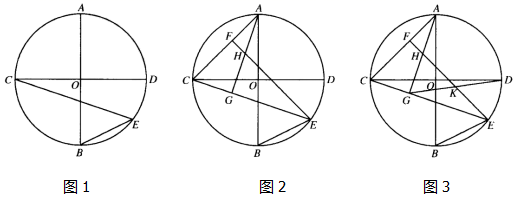 (1)、如图1,求证:AB⊥CD;(2)、如图2,连接AC,过点E作EF⊥AC,垂足为点F,过点A作AG⊥CE,垂足为点G,交EF于点H,求证:AC=EH;(3)、如图3,在(2)的条件下,连接DG,若∠DGE=∠CAG,BE=2 ,求EH的长.27. 已知:直线y=﹣ x+12交x轴于点A,交y轴于点B,经过点A的直线y= x+m交y轴于点C.
(1)、如图1,求证:AB⊥CD;(2)、如图2,连接AC,过点E作EF⊥AC,垂足为点F,过点A作AG⊥CE,垂足为点G,交EF于点H,求证:AC=EH;(3)、如图3,在(2)的条件下,连接DG,若∠DGE=∠CAG,BE=2 ,求EH的长.27. 已知:直线y=﹣ x+12交x轴于点A,交y轴于点B,经过点A的直线y= x+m交y轴于点C.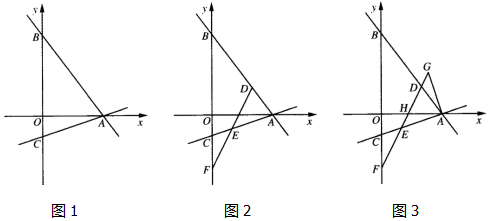 (1)、如图1,求点C的坐标;(2)、如图2,点D为线段AB上的一点,点E在线段AC上,连接DE,延长DE交y轴于点F,且DE=EF,设点D的横坐标为t,线段OF的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);(3)、如图3,在(2)的条件下,过点A作AG⊥AC,AG交ED的延长线于点G,DE交OA于点H,若DG=EH,求d的值.
(1)、如图1,求点C的坐标;(2)、如图2,点D为线段AB上的一点,点E在线段AC上,连接DE,延长DE交y轴于点F,且DE=EF,设点D的横坐标为t,线段OF的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);(3)、如图3,在(2)的条件下,过点A作AG⊥AC,AG交ED的延长线于点G,DE交OA于点H,若DG=EH,求d的值.