广东省深圳市2021年中考数学一模试卷
试卷更新日期:2021-05-08 类型:中考模拟
一、单选题
-
1. 在迎来庆祝新中国成立70周年之后,对于中国而言,2020年又将是一个新的时间坐标.过去40年,中国完成了卓越的经济转型,八亿两千万人成功脱贫,这是人类发展史上具有里程碑意义的重大成就.将820000000科学记数法表示为( )A、 B、 C、 D、2. 实数a,b,c在数轴上的对应点的位置如图所示,则下列结论正确的是( )
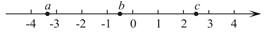 A、 B、 C、 D、3. 画如图所示物体的俯视图,正确的是( )
A、 B、 C、 D、3. 画如图所示物体的俯视图,正确的是( )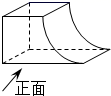 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、(﹣2a2b﹣1)2= B、(a+b)2=a2+b2 C、 ﹣3 =﹣2 D、 + =5. 某校男篮队员的年龄分布如表所示:
4. 下列运算正确的是( )A、(﹣2a2b﹣1)2= B、(a+b)2=a2+b2 C、 ﹣3 =﹣2 D、 + =5. 某校男篮队员的年龄分布如表所示:年龄/岁
13
14
15
人数
a
4﹣a
6
对于不同的a,下列关于年龄的统计量不会发生改变的是( )
A、平均数,中位数 B、众数,中位数 C、众数,方差 D、平均数,方差6. 商场将进价为100元的商品提高80%后标价,销售时按标价打折销售,结果仍获利44%,则这件商品销售时打几折( )A、7折 B、7.5折 C、8折 D、8.5折7. 以下说法正确的是( )A、三角形的外心到三角形三边的距离相等 B、顺次连接对角线相等的四边形各边中点所得的四边形是菱形 C、分式方程 的解为x=2 D、将抛物线y=2x2-2向右平移1个单位后得到的抛物线是y=2x2-38. 如图,平面直角坐标系xOy中,点A、B的坐标分别为(9,0)、(6,﹣9),△AB'O'是△ABO关于点A的位似图形,且O'的坐标为(﹣3,0),则点B'的坐标为( )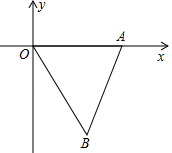 A、(8,﹣12) B、(﹣8,12) C、(8,﹣12)或(﹣8,12) D、(5,﹣12)9. 二次函数y=ax2+bx+c(a≠0)的顶点坐标为(﹣1,n),其部分图象如图所示,下面结论错误的是( )
A、(8,﹣12) B、(﹣8,12) C、(8,﹣12)或(﹣8,12) D、(5,﹣12)9. 二次函数y=ax2+bx+c(a≠0)的顶点坐标为(﹣1,n),其部分图象如图所示,下面结论错误的是( )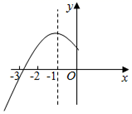 A、abc>0 B、4ac﹣b2<0 C、关于x的方程ax2+bx+c=n+1无实数根 D、关于x的方程ax2+bx+c=0的正实数根x1取值范围为:1<x1<210. 如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是( )
A、abc>0 B、4ac﹣b2<0 C、关于x的方程ax2+bx+c=n+1无实数根 D、关于x的方程ax2+bx+c=0的正实数根x1取值范围为:1<x1<210. 如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是( )
⑴EF= OE;
⑵S四边形OEBF:S正方形ABCD=1:4;
⑶BE+BF= OA;
⑷在旋转过程中,当△BEF与△COF的面积之和最大时,AE= ;
⑸OG•BD=AE2+CF2 .
A、(1)(2)(3)(5) B、(1)(3)(4)(5) C、(2)(3)(4)(5) D、(1)(2)(3)(4)二、填空题
-
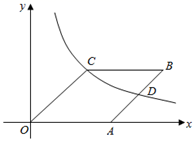
11. 因式分解:9a3b﹣ab=.12. 定义运算: ,若 , 是方程 的两个根,则 的值为 .13. 一个口袋中放有除颜色外,形状大小都相同的黑白两种球,黑球6个,白球10个.现在往袋中放入 个白球和4个黑球,使得摸到白球的概率为 ,则 .14. 在平面直角坐标系xOy中,A(0,2),B(0,6),动点C在直线y=﹣x上,若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数为 .15. 如图,在平面直角坐标系中,已知菱形OABC,点A的坐标为(3,0),点B,C均在第一象限,反比例函数y= (x>0)的图象经过点C,且与边AB交于点D,若D是AB的中点,则k的值为 .
三、解答题
-
16. 计算: .17. 先化简再求值:( +1)÷ ,其中a是方程a2+a=0的一个根.18. 面对突如其来的疫情,全国人民响应党和政府的号召,主动居家隔离.随之而来的,则是线上买菜需求激增.某小区为了解居民使用买菜APP的情况,通过制作无接触配送置物架,随机抽取了若干户居民进行调查(每户必选且只能选最常用的一个APP),现将调查结果绘制成如下两幅不完整的统计图;(A:天虹到家,B:叮咚买菜,C:每日优鲜,D:盒马鲜生)
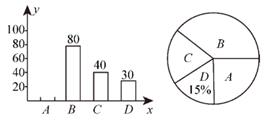 (1)、本次随机调查了户居民;(2)、补全条形统计图的空缺部分;(3)、若该小区共有1200户居民,请估计该小区居民选择“C:每日优鲜”的大约有户;(4)、某日下午, 张阿姨想购买苹果和生菜,各APP的供货情况如下:天虹到家仅有苹果在售,叮咚买菜仅有生菜在售,每日优鲜仅有生菜在售,盒马鲜生的苹果、生菜均已全部售完,则张阿姨随机选择两个不同的APP能买到苹果和生菜的概率是。19. 为了监控大桥下坡路段车辆行驶速度,通常会在下引桥处设置电子眼进行区间测速,如图,电子眼位于点P处,离地面的铅锤高度PQ为9米,区间测速的起点为下引桥坡面点A处,此时电子眼的俯角为30°;区间测速的中点为下引桥坡脚点B处,此时电子眼的俯角为60°(A、B、P、Q四点在同一平面).
(1)、本次随机调查了户居民;(2)、补全条形统计图的空缺部分;(3)、若该小区共有1200户居民,请估计该小区居民选择“C:每日优鲜”的大约有户;(4)、某日下午, 张阿姨想购买苹果和生菜,各APP的供货情况如下:天虹到家仅有苹果在售,叮咚买菜仅有生菜在售,每日优鲜仅有生菜在售,盒马鲜生的苹果、生菜均已全部售完,则张阿姨随机选择两个不同的APP能买到苹果和生菜的概率是。19. 为了监控大桥下坡路段车辆行驶速度,通常会在下引桥处设置电子眼进行区间测速,如图,电子眼位于点P处,离地面的铅锤高度PQ为9米,区间测速的起点为下引桥坡面点A处,此时电子眼的俯角为30°;区间测速的中点为下引桥坡脚点B处,此时电子眼的俯角为60°(A、B、P、Q四点在同一平面).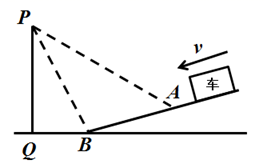 (1)、求路段BQ的长(结果保留根号);(2)、当下引桥坡度 时,求电子眼区间测速路段AB的长(结果保留根号).20. 纸箱厂用如图1所示的长方形和正方形纸板,做成如图2所示的竖式与横式两种长方体形状的有底无盖纸盒(给定的长方形和正方形纸板都不用裁剪).
(1)、求路段BQ的长(结果保留根号);(2)、当下引桥坡度 时,求电子眼区间测速路段AB的长(结果保留根号).20. 纸箱厂用如图1所示的长方形和正方形纸板,做成如图2所示的竖式与横式两种长方体形状的有底无盖纸盒(给定的长方形和正方形纸板都不用裁剪).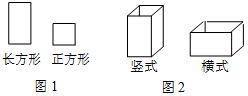 (1)、若有150张正方形硬纸片和300张长方形硬纸片恰好全部用完,可供制作竖式与横式纸盒各多少个?(2)、现有正方形纸板172张,长方形纸板330张. 若要生产两种纸盒共100个.已知每个竖式纸盒可获利2元,每个横式纸盒可获利3元.应如何安排生产,可使销售利润最大?最大利润是多少?(3)、若有正方形纸板112张,长方形纸板a张,做成上述两种纸盒,纸板恰好用完.若已知200<a<210,则a的值是 . (直接写答案)21. 在平面直角坐标系 中,把与x轴交点相同的二次函数图象称为“共根抛物线”.如图,抛物线 的顶点为D,交x轴于点A、B(点A在点B左侧),交y轴于点C.抛物线 与 是“共根抛物线”,其顶点为P.
(1)、若有150张正方形硬纸片和300张长方形硬纸片恰好全部用完,可供制作竖式与横式纸盒各多少个?(2)、现有正方形纸板172张,长方形纸板330张. 若要生产两种纸盒共100个.已知每个竖式纸盒可获利2元,每个横式纸盒可获利3元.应如何安排生产,可使销售利润最大?最大利润是多少?(3)、若有正方形纸板112张,长方形纸板a张,做成上述两种纸盒,纸板恰好用完.若已知200<a<210,则a的值是 . (直接写答案)21. 在平面直角坐标系 中,把与x轴交点相同的二次函数图象称为“共根抛物线”.如图,抛物线 的顶点为D,交x轴于点A、B(点A在点B左侧),交y轴于点C.抛物线 与 是“共根抛物线”,其顶点为P.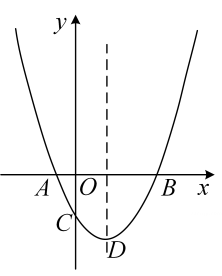
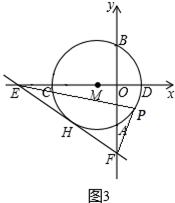
 (1)、若抛物线 经过点 ,求 对应的函数表达式;(2)、当 的值最大时,求点P的坐标;(3)、设点Q是抛物线 上的一个动点,且位于其对称轴的右侧.若 与 相似,求其“共根抛物线” 的顶点P的坐标.22. 如图1所示,以点M(−1,0)为圆心的圆与y轴,x轴分别交于点A,B,C,D,与⊙M相切于点H的直线EF交x轴于点E( ,0),交y轴于点F(0, ).
(1)、若抛物线 经过点 ,求 对应的函数表达式;(2)、当 的值最大时,求点P的坐标;(3)、设点Q是抛物线 上的一个动点,且位于其对称轴的右侧.若 与 相似,求其“共根抛物线” 的顶点P的坐标.22. 如图1所示,以点M(−1,0)为圆心的圆与y轴,x轴分别交于点A,B,C,D,与⊙M相切于点H的直线EF交x轴于点E( ,0),交y轴于点F(0, ).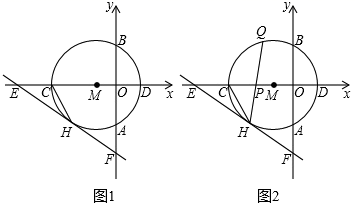 (1)、求⊙M的半径r;(2)、如图2所示,连接CH,弦HQ交x轴于点P,若cos∠QHC= ,求 的值;(3)、如图3所示,点P为⊙M上的一个动点,连接PE,PF,求PF+ PE的最小值.
(1)、求⊙M的半径r;(2)、如图2所示,连接CH,弦HQ交x轴于点P,若cos∠QHC= ,求 的值;(3)、如图3所示,点P为⊙M上的一个动点,连接PE,PF,求PF+ PE的最小值.