广东省广州市天河区2021年中考数学一模试卷
试卷更新日期:2021-05-08 类型:中考模拟
一、单选题
-
1. 2021的相反数是( )A、 B、2021 C、 D、2. 下面图形是用数学家名字命名的,其中是中心对称图形但不是轴对称图形的是( )A、
 赵爽弦图
B、
赵爽弦图
B、 笛卡尔心形线
C、
笛卡尔心形线
C、 科克曲线
D、
科克曲线
D、 斐波那契螺旋线
3. 人民网北京2021年1月7日电,截至1月3日6时,我国首次火星探测任务天问一号火星探测器已经在轨飞行约163天,飞行里程突破4亿公里,距离地球接近1.3亿公里,距离火星约830万公里.数据830万公里用科学记数法表示为( )
斐波那契螺旋线
3. 人民网北京2021年1月7日电,截至1月3日6时,我国首次火星探测任务天问一号火星探测器已经在轨飞行约163天,飞行里程突破4亿公里,距离地球接近1.3亿公里,距离火星约830万公里.数据830万公里用科学记数法表示为( ) A、8.3×106公里 B、8.3×105公里 C、8.3×104公里 D、0.83×106公里4. 已知 O与点P在同一平面内,如果 O的直径为6,线段OP的长为4,则下列说法正确的是( )A、点P在 O上 B、点P在 O内 C、点P在 O外 D、无法判断点P与 O的位置关系5. 下列运算正确的是( )A、 B、 C、 D、6. 若方程x2-cx+4=0有两个不相等的实数根,则c的值不能是( )A、c=10 B、c=5 C、c=-5 D、c=47. 若分式 的值为0,则x的值为( )A、-5 B、5 C、-5和5 D、无法确定8. 已知a= ,b= ,则a2+b2的值为( )A、8 B、1 C、6 D、9. 二次函数y=ax2+bx+c的图象如图所示,反比例函数y= 与正比例函数y=(2a+c)x在同一坐标系内的大致图象是( )
A、8.3×106公里 B、8.3×105公里 C、8.3×104公里 D、0.83×106公里4. 已知 O与点P在同一平面内,如果 O的直径为6,线段OP的长为4,则下列说法正确的是( )A、点P在 O上 B、点P在 O内 C、点P在 O外 D、无法判断点P与 O的位置关系5. 下列运算正确的是( )A、 B、 C、 D、6. 若方程x2-cx+4=0有两个不相等的实数根,则c的值不能是( )A、c=10 B、c=5 C、c=-5 D、c=47. 若分式 的值为0,则x的值为( )A、-5 B、5 C、-5和5 D、无法确定8. 已知a= ,b= ,则a2+b2的值为( )A、8 B、1 C、6 D、9. 二次函数y=ax2+bx+c的图象如图所示,反比例函数y= 与正比例函数y=(2a+c)x在同一坐标系内的大致图象是( ) A、
A、 B、
B、 C、
C、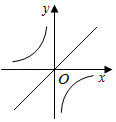 D、
D、 10. 尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作图考他的大臣:
10. 尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作图考他的大臣:①将半径为r的⊙O六等分,依次得到A,B,C,D,E,F六个分点;②分别以点A,D为圆心,AC长为半径画弧,G是两弧的一个交点;③连结OG.问:OG的长是多少?大臣给出的正确答案应是( )
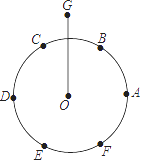 A、 r B、(1+ )r C、(1+ )r D、 r
A、 r B、(1+ )r C、(1+ )r D、 r二、填空题
-
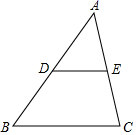
11. 分解因式:x2+3x= .12. 样本数据1,5,n,6,8的众数是1,则这组数的中位数是 .13. 如图,在 中,D,E分别是边 , 的中点.若 的面积为 .则四边形 的面积为 .
 14. 已知圆锥的底面半径为2cm,侧面积为10πcm2 , 则该圆锥的母线长为cm.15. 在Rt ABC中,∠C=90°,sinB= ,若斜边上的高CD=2,则AC= .16. 如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于E,点G是AE中点且∠AOG=30°.某班学习委员得到四个结论:①DC=3OG;②OG= BC;③ OGE是等边三角形;④S△AOE= S矩形ABCD , 问:学习委员得到结论正确的是 . (填写所有正确结论的序号)
14. 已知圆锥的底面半径为2cm,侧面积为10πcm2 , 则该圆锥的母线长为cm.15. 在Rt ABC中,∠C=90°,sinB= ,若斜边上的高CD=2,则AC= .16. 如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于E,点G是AE中点且∠AOG=30°.某班学习委员得到四个结论:①DC=3OG;②OG= BC;③ OGE是等边三角形;④S△AOE= S矩形ABCD , 问:学习委员得到结论正确的是 . (填写所有正确结论的序号)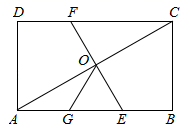
三、解答题
-
17. 解方程组:18. 已知:如图,AB∥ED,点F、点C在AD上,AB=DE,AF=DC.求证:BC=EF.
 19. 五一期间,甲、乙两人计划在附近的景点游玩,甲从A、B两个景点中任意选择一个游玩,乙从A、B、C三个景点中任意选择一个游玩.(1)、填空:乙恰好游玩A景点的概率为 .(2)、求甲、乙恰好游玩同一景点的概率.20. 创建文明城市,携手共建幸福美好.某地为美化环境,计划种植树木4800棵,由于志愿者的加入,实际每天植树的棵数比原计划多20%,结果提前4天完成任务.求原计划每天植树的棵数.21. 如图,在Rt ABC中,∠BCA=90°,∠A=30°.
19. 五一期间,甲、乙两人计划在附近的景点游玩,甲从A、B两个景点中任意选择一个游玩,乙从A、B、C三个景点中任意选择一个游玩.(1)、填空:乙恰好游玩A景点的概率为 .(2)、求甲、乙恰好游玩同一景点的概率.20. 创建文明城市,携手共建幸福美好.某地为美化环境,计划种植树木4800棵,由于志愿者的加入,实际每天植树的棵数比原计划多20%,结果提前4天完成任务.求原计划每天植树的棵数.21. 如图,在Rt ABC中,∠BCA=90°,∠A=30°. (1)、用尺规作AB的垂直平分线交AC于点D,并作∠CBA的平分线BM;(不写作法,保留作图痕迹)(2)、你认为(1)中的点D在射线BM上吗?请说明理由.22. 如图,直线MN与 O相切于点M,ME=EF且EF//MN.
(1)、用尺规作AB的垂直平分线交AC于点D,并作∠CBA的平分线BM;(不写作法,保留作图痕迹)(2)、你认为(1)中的点D在射线BM上吗?请说明理由.22. 如图,直线MN与 O相切于点M,ME=EF且EF//MN. (1)、求cos∠E的值:(2)、若 O的半径为2.求图中阴影部分的面积.23. 如图,四边形ABCO是平行四边形,AO=2,AB=6,点A在第一象限,点C在x轴的负半轴上,将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF,点D在反比例函数 的图象上,且AD经过点O,点F恰好落在x轴的正半轴上.
(1)、求cos∠E的值:(2)、若 O的半径为2.求图中阴影部分的面积.23. 如图,四边形ABCO是平行四边形,AO=2,AB=6,点A在第一象限,点C在x轴的负半轴上,将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF,点D在反比例函数 的图象上,且AD经过点O,点F恰好落在x轴的正半轴上.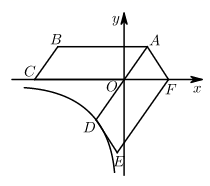 (1)、求点A的坐标;(2)、求k的值.24. 已知抛物线y=mx2-2mx+3(m<0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,且OB=3OA.(1)、求抛物线的解析式:(2)、若M,N是第一象限的抛物线上不同的两点,且ΔBCN的面积恒小于 BCM的面积,求点M的坐标;(3)、若D为抛物线的顶点,P为第二象限的抛物线上的一点,连接BP,DP,分别交y轴于E,F,若EF= OC,求点P的坐标.25. 如图,ΔABC中,∠BAC 120°,AB=AC,点A关于直线BC的对称点为点D,连接BD,CD.
(1)、求点A的坐标;(2)、求k的值.24. 已知抛物线y=mx2-2mx+3(m<0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,且OB=3OA.(1)、求抛物线的解析式:(2)、若M,N是第一象限的抛物线上不同的两点,且ΔBCN的面积恒小于 BCM的面积,求点M的坐标;(3)、若D为抛物线的顶点,P为第二象限的抛物线上的一点,连接BP,DP,分别交y轴于E,F,若EF= OC,求点P的坐标.25. 如图,ΔABC中,∠BAC 120°,AB=AC,点A关于直线BC的对称点为点D,连接BD,CD.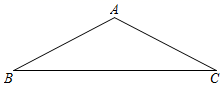 (1)、求证:四边形ABDC是菱形;(2)、延长CA到E,使得AB=BE.求证:BC2-AC·CE=AC2;(3)、在(2)小题条件下,可知E,B,D,C四点在同一个圆上,设其半径为a(定值),若BC=kAB,问k取何值时,BE·CE的值最大?
(1)、求证:四边形ABDC是菱形;(2)、延长CA到E,使得AB=BE.求证:BC2-AC·CE=AC2;(3)、在(2)小题条件下,可知E,B,D,C四点在同一个圆上,设其半径为a(定值),若BC=kAB,问k取何值时,BE·CE的值最大?