广东省佛山市南海区2021年中考数学一模试卷
试卷更新日期:2021-05-08 类型:中考模拟
一、单选题
-
1. 实数2021的相反数是( )A、2021 B、 C、 D、2. 在平面直角坐标系中,已知点 的坐标是 ,那么点 关于 轴对称的点 的坐标是( )A、 B、 C、 D、3. 如图所示,用量角器度量 ,那么 的补角度数为( )
 A、 B、 C、 D、4. 下列关于事情发生的可能性,说法正确的是( )A、可能性很大的事情必然发生 B、可能性很小的事情一定不会发生 C、投掷一枚均匀的正方体骰子,掷得的点数是奇数的可能性比掷得的点数是偶数的可能性大 D、投掷一枚均匀的正方体骰子,结果骰子的点数恰好是“3”的可能性大小是5. 若分式 无意义,则x的取值范围是( )A、 B、 C、 D、6. 如图,以点 为圆心,任意长为半径画弧,分别交 于点 .分别以 两点为圆心, 长为半径画弧,两段弧交于点 ,作射线 ,连接 ,则 与 全等,其全等的判定依据是( )
A、 B、 C、 D、4. 下列关于事情发生的可能性,说法正确的是( )A、可能性很大的事情必然发生 B、可能性很小的事情一定不会发生 C、投掷一枚均匀的正方体骰子,掷得的点数是奇数的可能性比掷得的点数是偶数的可能性大 D、投掷一枚均匀的正方体骰子,结果骰子的点数恰好是“3”的可能性大小是5. 若分式 无意义,则x的取值范围是( )A、 B、 C、 D、6. 如图,以点 为圆心,任意长为半径画弧,分别交 于点 .分别以 两点为圆心, 长为半径画弧,两段弧交于点 ,作射线 ,连接 ,则 与 全等,其全等的判定依据是( ) A、 B、 C、 D、7. 如图,一次函数 的图象经过点 ,则下列说法正确的是( )
A、 B、 C、 D、7. 如图,一次函数 的图象经过点 ,则下列说法正确的是( ) A、 B、 C、方程 的解是 D、 随 的增大而减小8. 如图,现有一等腰直角三角形 的腰长为4, ,将 沿 折叠,使 的顶点恰好落在 边的中点 处,则线段 的长度为( )
A、 B、 C、方程 的解是 D、 随 的增大而减小8. 如图,现有一等腰直角三角形 的腰长为4, ,将 沿 折叠,使 的顶点恰好落在 边的中点 处,则线段 的长度为( ) A、 B、 C、 D、9. 已知Rt 的两条直角边的长度恰好是一元二次方程 的两个实数根,那么 的面积为( )A、16 B、32 C、 D、10. 如图,已知二次函数 的图象交 轴于 两点,交 轴于点 ,对称轴为直线 .直线 与二次函数的图象交于 两点, 点在 轴的下方,而且 的横坐标小于4,下列结论:
A、 B、 C、 D、9. 已知Rt 的两条直角边的长度恰好是一元二次方程 的两个实数根,那么 的面积为( )A、16 B、32 C、 D、10. 如图,已知二次函数 的图象交 轴于 两点,交 轴于点 ,对称轴为直线 .直线 与二次函数的图象交于 两点, 点在 轴的下方,而且 的横坐标小于4,下列结论:① ;② ;③ ;④不等式 的取值范围是 .其中正确的结论有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
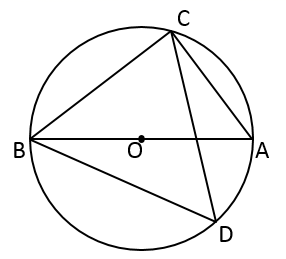
11. 分解因式: .12. 一个正多边形的每一个外角都等于36 , 则这个多边形的边数是 .13. 已知 ,那么 .14. 不等式组 的解集为 .15. 如图, 是⊙O的直径, 是直径 两侧⊙O上的点,若 ,那么 的度数为°.
 16. 已知当 时,代数式 的值为3,那么代数式 的值为 .17. 如图,在平面直角坐标系中,点 的坐标是 ,点 的坐标是 ,点 是 轴上的一个动点,作 ,垂足为点 ,连 ,则 的面积的最大值为 .
16. 已知当 时,代数式 的值为3,那么代数式 的值为 .17. 如图,在平面直角坐标系中,点 的坐标是 ,点 的坐标是 ,点 是 轴上的一个动点,作 ,垂足为点 ,连 ,则 的面积的最大值为 .
三、解答题
-
18. 计算: .19. 某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图,如图所示:

 (1)、求本次调查的学生总人数,并补全条形统计图;(2)、该校共有学生3000人,请你估计该校对在线阅读最感兴趣的学生人数.20. 如图,在平行四边形 中,点 在 上,点 在 上,且 ,点 在 上,且 ,连接 .求证:四边形 是平行四边形.
(1)、求本次调查的学生总人数,并补全条形统计图;(2)、该校共有学生3000人,请你估计该校对在线阅读最感兴趣的学生人数.20. 如图,在平行四边形 中,点 在 上,点 在 上,且 ,点 在 上,且 ,连接 .求证:四边形 是平行四边形.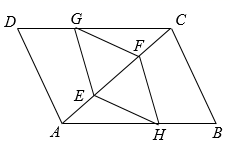 21. 如图,一次函数 的图像与 轴交于点 ;一次函数 的图像与 轴交于点 ,且经过点 ,两函数图象交于点 .
21. 如图,一次函数 的图像与 轴交于点 ;一次函数 的图像与 轴交于点 ,且经过点 ,两函数图象交于点 .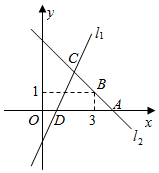 (1)、求 , , 的值;(2)、根据图象,直接写出 的解集.22. 春节期间,佛山连锁超市派调查小组调查某种商品的销售情况,下面是调查后小李与其他两位成员交流的情况.
(1)、求 , , 的值;(2)、根据图象,直接写出 的解集.22. 春节期间,佛山连锁超市派调查小组调查某种商品的销售情况,下面是调查后小李与其他两位成员交流的情况.小李:“该商品的进价为50元/件.”
成员甲:“当定价为60元/件时,平均每天可售出800件.”
成员乙:“若售价每提高5元,则平均每天少售出100件.”
根据他们的对话,完成下列问题:
(1)、若售价定为65元/件时,平均每天可售出件;(2)、若超市希望该商品平均每天能盈利12000元,且尽可能扩大销售量,则该商品应该怎样定价?23. 如图,圆内接正方形 是圆弧 上的一点,连接 ,线段 上有一点 ,连接 ,且 . (1)、求证: .(2)、连接 ,当四边形 是平行四边形时,求 的值.24. 如图1,在平面直角坐标系中,直线 与双曲线 交于点 和点 ,连接 ,其中 .
(1)、求证: .(2)、连接 ,当四边形 是平行四边形时,求 的值.24. 如图1,在平面直角坐标系中,直线 与双曲线 交于点 和点 ,连接 ,其中 . (1)、求双曲线和直线 的表达式;(2)、求 的面积;(3)、如图2,将直线 沿着 轴向下平移得到直线 ,且直线 与双曲线在第三象限内的交点为 ,若 的面积为20,求直线 与 轴的交点坐标.25. 如图,在平面直角坐标系 中,四边形 是矩形,点 的坐标是 ,点 为 边上的一动点(不与点 重合),连接 ,过点 作直线 ,交 于点 ,在直线 上取一点 (点 在点 右侧),使得 ,过点 作 ,交 于点 ,连接 ,设 .
(1)、求双曲线和直线 的表达式;(2)、求 的面积;(3)、如图2,将直线 沿着 轴向下平移得到直线 ,且直线 与双曲线在第三象限内的交点为 ,若 的面积为20,求直线 与 轴的交点坐标.25. 如图,在平面直角坐标系 中,四边形 是矩形,点 的坐标是 ,点 为 边上的一动点(不与点 重合),连接 ,过点 作直线 ,交 于点 ,在直线 上取一点 (点 在点 右侧),使得 ,过点 作 ,交 于点 ,连接 ,设 . (1)、填空:点 的坐标为(用含 的代数式表示);(2)、判断线段 的长度是否随点 的位置的变化而变化?并说明理由;(3)、①当 为何值时,四边形 的面积最小,请求出最小值;
(1)、填空:点 的坐标为(用含 的代数式表示);(2)、判断线段 的长度是否随点 的位置的变化而变化?并说明理由;(3)、①当 为何值时,四边形 的面积最小,请求出最小值;②在 轴正半轴上存在点 ,使得 是等腰三角形,请直接写出3个符合条件的点 的坐标(用含 的代数式表示).