广东省佛山市桂城街道2021年中考数学模拟试卷
试卷更新日期:2021-05-08 类型:中考模拟
一、单选题
-
1. 2021的倒数是( )A、 B、 C、2021 D、2. 为在2020年实现全面建成小康社会的目标任务,自2016年以来,广东已向西部四省拔付财政资金105.8亿元援助脱贫攻坚项目.数据105.8亿用科学记数法表示为( )A、 B、 C、 D、3. 一个不透明的布袋里装有7个只有颜色不同的球,其中4个白球,2个红球,1个黄球。从布袋里任意摸出1个球,是红球的概率为( )A、 B、 C、 D、4. 在 中, , 平分 ,交 于点D, ,垂足为点E,若 ,则 的长为( )
 A、3 B、 C、2 D、65. 泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度。金字塔的影长,推算出金字塔的高度。这种测量原理,就是我们所学的( )
A、3 B、 C、2 D、65. 泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度。金字塔的影长,推算出金字塔的高度。这种测量原理,就是我们所学的( ) A、图形的平移 B、图形的旋转 C、图形的轴对称 D、图形的相似6. 一副直角三角板如图放置,点C在FD的延长线上,AB//CF,∠F=∠ACB=90°,则∠DBC的度数为( )
A、图形的平移 B、图形的旋转 C、图形的轴对称 D、图形的相似6. 一副直角三角板如图放置,点C在FD的延长线上,AB//CF,∠F=∠ACB=90°,则∠DBC的度数为( ) A、10° B、15° C、18° D、30°7. 下列等式成立的是( )A、 B、 C、 D、8. 已知m、n、4分别是等腰三角形(非等边三角形)三边的长,且m、n是关于x的一元二次方程 ﹣6x+k+2=0的两个根,则k的值等于( )A、7 B、7或6 C、6或﹣7 D、69. 如图,在矩形 中, 为边 上一点,将 沿直线 翻折,使得点 的对应点 落在 边上.若 ,则 的长度是( )
A、10° B、15° C、18° D、30°7. 下列等式成立的是( )A、 B、 C、 D、8. 已知m、n、4分别是等腰三角形(非等边三角形)三边的长,且m、n是关于x的一元二次方程 ﹣6x+k+2=0的两个根,则k的值等于( )A、7 B、7或6 C、6或﹣7 D、69. 如图,在矩形 中, 为边 上一点,将 沿直线 翻折,使得点 的对应点 落在 边上.若 ,则 的长度是( ) A、 B、 C、 D、110. 如图,点 是以 为直径的半圆上的动点, 于点 ,连接 ,设 ,则下列函数图象能反映 与 之间关系的是( )
A、 B、 C、 D、110. 如图,点 是以 为直径的半圆上的动点, 于点 ,连接 ,设 ,则下列函数图象能反映 与 之间关系的是( )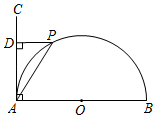 A、
A、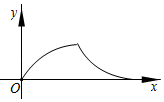 B、
B、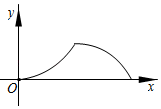 C、
C、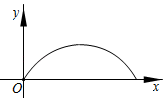 D、
D、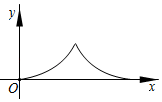
二、填空题
-
11. 分解因式:2a3﹣8a= .12. 使分式 有意义的x的取值范围是.13. 不等式组 的解集是.14. 某个函数具有性质:当 >0时, 随 的增大而增大,这个函数的表达式可以是(只要写出一个正确的答案即可)15. 如图,在平面直角坐标系中,在x轴、y轴的正半轴上分别截取OA、OB,使OA=OB;再分别以点A、B为圆心,以大于 长为半径作弧,两弧交于点P.若点C的坐标为( ),则a的值为 .
 16. 如图,在边长为3的菱形 中, , 是 边上的一点,且 , 是 边上的一动点,将 沿 所在直线翻折得到 ,连接 .则 长度的最小值是 .
16. 如图,在边长为3的菱形 中, , 是 边上的一点,且 , 是 边上的一动点,将 沿 所在直线翻折得到 ,连接 .则 长度的最小值是 .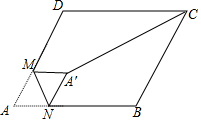 17. 如图,在矩形 中, ,一发光电子开始置于 边的点 处,并设定此时为发光电子第一次与矩形的边碰撞,将发光电子沿着 方向发射,碰撞到矩形的边时均反射,每次反射的反射角和入射角都等于45°,若发光电子与矩形的边碰撞次数经过2021次后,则它与 边的碰撞次数是 .
17. 如图,在矩形 中, ,一发光电子开始置于 边的点 处,并设定此时为发光电子第一次与矩形的边碰撞,将发光电子沿着 方向发射,碰撞到矩形的边时均反射,每次反射的反射角和入射角都等于45°,若发光电子与矩形的边碰撞次数经过2021次后,则它与 边的碰撞次数是 .
三、解答题
-
18. 计算:19. 先化简,再求值: ,其中 .20. 为了解全校学生对“垃圾分类”知识的掌握情况,某初级中学的两个兴趣小组分别抽样调查了100名学生.为方便制作统计图表,对“垃圾分类”知识的掌握情况分成四个等级:A表示“优秀”,B表示“良好”,C表示“合格”,D表示“不合格”.第一小组认为,八年级学生对“垃圾分类”知识的掌握不如九年级学生,但好于七年级学生,所以他们随机调查了100名八年级学生.
第二小组随机调查了全校三个年级中的100名学生,但只收集到90名学生的有效问卷调查表.
两个小组的调查结果如图的图表所示:
第二小组统计表
等级
人数
百分比
A
17
18.9%
B
38
42.2%
C
28
31.1%
D
7
7.8%
合计
90
100%

若该校共有1000名学生,试根据以上信息解答下列问题:
(1)、第小组的调查结果比较合理,用这个结果估计该校学生对“垃圾分类”知识掌握情况达到合格以上(含合格)的共约人;(2)、对这两个小组的调查统计方法各提一条改进建议.21. “绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)、求该型号自行车的进价和标价分别是多少元?
(2)、若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价20元,每月可多售出3辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
22.(1)、小迪同学在学习圆的内接正多边形时,发现:如图1,若 是圆内接正三角形 的外接圆的 上任一点,则 ,在 上截取 ,连接 ,可证明 是(填“等腰”、“等边”或“直角”)三角形,从而得到 ,再进一步证明 , 得到 ,可证得: (2)、小迪同学对以上推理进行类比研究,发现:如图2,若 是圆内接正四边形 的外接圆的 上任一点,则 °,分别过点 作 于 、 于 .(3)、写出 与 之间的数量关系,并说明理由.23. 如图, 为反比例函数 (x>0)图象上的一点,在 轴正半轴上有一点 , .连接 , ,且 .
(2)、小迪同学对以上推理进行类比研究,发现:如图2,若 是圆内接正四边形 的外接圆的 上任一点,则 °,分别过点 作 于 、 于 .(3)、写出 与 之间的数量关系,并说明理由.23. 如图, 为反比例函数 (x>0)图象上的一点,在 轴正半轴上有一点 , .连接 , ,且 .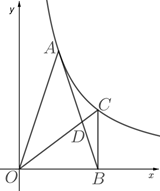 (1)、求 的值;(2)、过点 作 ,交反比例函数 (x>0)的图象于点 ,连接 交 于点 ,求 的值.24. 如图1, 分别是 的内角 的平分线,过点 作 ,交 的延长线于点 .
(1)、求 的值;(2)、过点 作 ,交反比例函数 (x>0)的图象于点 ,连接 交 于点 ,求 的值.24. 如图1, 分别是 的内角 的平分线,过点 作 ,交 的延长线于点 . (1)、求证: ;(2)、如图2,如果 ,且 ,求 的值;(3)、如果 是锐角,且 与 相似,求 的度数,并直接写出 的值.25. 如图,二次函数 的图象过原点,与 轴的另一个交点为
(1)、求证: ;(2)、如图2,如果 ,且 ,求 的值;(3)、如果 是锐角,且 与 相似,求 的度数,并直接写出 的值.25. 如图,二次函数 的图象过原点,与 轴的另一个交点为 (1)、求该二次函数的解析式;(2)、在 轴上方作 轴的平行线 ,交二次函数图象于 、 两点,过 、 两点分别作 轴的垂线,垂足分别为点 、点 .矩形 为正方形,求 的值;(3)、在(2)的条件下,动点 从点 出发沿射线 以每秒1个单位长度匀速运动,同时动点 以相同的速度从点 出发沿线段 匀速运动,到达点 时立即原速返回,当动点 返回到点 时, 、 两点同时停止运动,设运动时间为 秒( ).过点 向 轴作垂线,交抛物线于点 ,交直线 于点 ,当以 、 、 、 四点为顶点构成的四边形为平行四边形时,请求出 的值.
(1)、求该二次函数的解析式;(2)、在 轴上方作 轴的平行线 ,交二次函数图象于 、 两点,过 、 两点分别作 轴的垂线,垂足分别为点 、点 .矩形 为正方形,求 的值;(3)、在(2)的条件下,动点 从点 出发沿射线 以每秒1个单位长度匀速运动,同时动点 以相同的速度从点 出发沿线段 匀速运动,到达点 时立即原速返回,当动点 返回到点 时, 、 两点同时停止运动,设运动时间为 秒( ).过点 向 轴作垂线,交抛物线于点 ,交直线 于点 ,当以 、 、 、 四点为顶点构成的四边形为平行四边形时,请求出 的值.