安徽省铜陵市义安区2021年中考数学一模试卷

试卷更新日期：2021-05-08 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣2的倒数为（）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、﹣2 D、2

查看试题解析
2. “概率”的英文单词是“Probability”，如果在组成该单词的所有字母中任意取出一个字母，则取到字母“b”的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{11}$ C、 $\frac{2}{11}$ D、1

查看试题解析
3. 2020年11月24日4时30分，我国在文昌航天发射场成功发射“嫦娥五号”探测器，实现人类航天史上第一次在38万公里外的月球轨道上进行了无人交会对接，将数据38万公里用科学记数法表示为（）

A、 $3.8 \times 10^{7}$ 米 B、 $38 \times 10^{7}$ 米 C、 $3.8 \times 10^{8}$ 米 D、 $0.38 \times 10^{9}$ 米

查看试题解析
4. 如图，在 $△ A B C$ 中， $∠ B A C = 40 °$ ， $∠ B = 60 °$ ， $A D // B C$ ，则 $∠ D A C$ 大小为（）

A、 $20 °$ B、 $40 °$ C、 $60 °$ D、 $80 °$

查看试题解析
5. 已知点 $A (a ， b)$ 和点 $B (a + 1 ， b^{'})$ 都在正比例函数 $y = 3 x$ 图象上，则 $b^{'} - b$ 的值为（）

A、 $- 3$ B、 $- 2$ C、 $3$ D、 $2$

查看试题解析
6. 如图在△ABC中，AC＝BC，过点C作CD⊥AB，垂足为点D，过D作DE∥BC交AC于点E，若BD＝6，AE＝5，则sin∠EDC的值为（）

A、 $\frac{3}{5}$ B、 $\frac{7}{25}$ C、 $\frac{4}{5}$ D、 $\frac{24}{25}$

查看试题解析
7. 在平面直角坐标系中，将函数 $y = 3 x$ 的图象向上平移 $m$ 个单位长度，使其与 $y = - 3 x + 6$ 的交点在位于第二象限，则 $m$ 的取值范围为（）

A、 $m < 6$ B、 $m > 6$ C、 $m < 2$ D、 $m > 2$

查看试题解析
8. 如图，菱形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点 $O$ ， $∠ A B D = 30 °$ ， $B C = 4$ ，则边 $A D$ 与 $B C$ 之间的距离为（）

A、 $2 \sqrt{5}$ B、 $2 \sqrt{3}$ C、 $\sqrt{5}$ D、 $\sqrt{3}$

查看试题解析
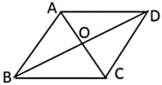9. 如图，⊙O的弦AB与CD交于点E，点F在AB上，且FD∥BC，若∠AFD＝125°，则∠ADC的度数为（）

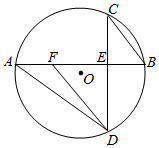A、60° B、55° C、50° D、45°

查看试题解析
10. 在平面直角坐标系中，一个智能机器人接到如下指令：从原点O出发，按向右，向上，向右，向下的方向依次不断移动，每次移动1m．其行走路线如图所示，第1次移动到A₁ ，第2次移动到A₂ ， …，第n次移动到A_n ．则△OA₂A₂₀₂₁的面积是（）

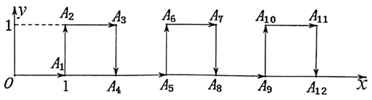A、505.5 m² B、505 m² C、504.5 m² D、506 m²

查看试题解析

二、填空题

11. 分解因式：ax²﹣4ay²= ．

查看试题解析
12. 如图，点A在函数y＝ $\frac{k}{x}$ 的图象上，AB⊥y轴于点B，S_△AOB＝2.5，则k＝．

查看试题解析
13. 如图，P、Q分别是⊙O的内接正五边形的边AB、BC上的点，BP=CQ，则∠POQ= ．

查看试题解析
14. 把两个同样大小的含45°角的三角尺按如图所示的方式放置，其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A，且另三个锐角顶点B，C，D在同一直线上．若AB= $\sqrt{2}$ ，则CD= ．

查看试题解析

三、解答题

15. 先化简，再求值：（ $\frac{2 a}{a^{2} - 1}$ ﹣ $\frac{1}{a + 1}$ ）÷ $\frac{a + 2}{a^{2} - 1}$ ，其中a＝ $\sqrt{5}$ ．

查看试题解析
16. 《孙子算经》中有过样一道题，原文如下： “今有百鹿入城，家取一鹿不尽，又三家共一鹿适尽，问城中家几何？” 大意为：今有100头鹿进城，每家取一头鹿，没有取完，剩下的鹿每3家共取一头，恰好取完，问城中有多少户人家？请解答上述问题.

查看试题解析
17. 如图，在 $△ A B C$ 中，点 $E$ 在 $A B$ 边上，请用尺规作图法在 $A C$ 边上求作一点 $F$ ，使得 $F E = F C$ ．（不写作法，保留作图痕迹）

查看试题解析
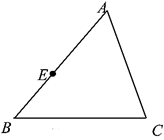18. 如图，AB、AC分别是⊙O的直径和弦，OD⊥AC于点D，过点A作⊙O的切线与OD的延长线交于点P，PC、AB的延长线交于点F.

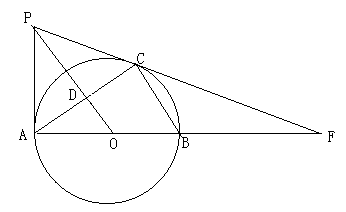(1)、求证：PC是⊙O的切线；

(2)、若∠ABC=60°，AB=10，求线段CF的长，

查看试题解析
19. 观察以下等式：
第1个等式： $\frac{2}{1} = \frac{1}{1} + \frac{1}{1}$ ，

第2个等式： $\frac{2}{3} = \frac{1}{2} + \frac{1}{6}$ ，

第3个等式： $\frac{2}{5} = \frac{1}{3} + \frac{1}{15}$ ，

第4个等式： $\frac{2}{7} = \frac{1}{4} + \frac{1}{28}$ ，

第5个等式： $\frac{2}{9} = \frac{1}{5} + \frac{1}{45}$ ，

……按照以上规律，解决下列问题：

(1)、写出第6个等式：；

(2)、写出你猜想的第n个等式(用含n的等式表示)，并证明.

查看试题解析
20. 如图，某数学兴趣小组为测量一棵古树BH和教学楼CG的高，先在A处用高1.5米的测角仪测得古树顶端H的仰角∠HDE为45°，此时教学楼顶端G恰好在视线DH上，再向前走7米到达B处，又测得教学楼顶端G的仰角∠GEF为60°，点A、B、C三点在同一水平线上．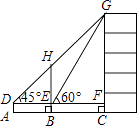

(1)、计算古树 BH的高；

(2)、计算教学楼CG的高．（参考数据： $\sqrt{2}$ ≈14， $\sqrt{3}$ ≈1.7）

查看试题解析
21. 某学校为调查学生的兴趣爱好，抽查了部分学生，并制作了如下表格与条形统计图：

频数
频率
体育
40
0.4
科技
25
$a$
艺术
$b$
0.15
其它
20
0.2

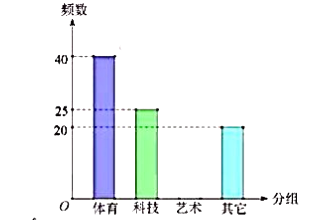
请根据上图完成下面题目：

(1)、总人数为人， $a =$ ， $b =$ .

(2)、请你补全条形统计图.

(3)、若全校有600人，请你估算一下全校喜欢艺术类学生的人数有多少？

查看试题解析
22. 某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于45%，经试销发现，销售量y（件）与销售单价x（元）符合一次函数y=kx+b，且x=65时，y=55；x=75时，y=45．

(1)、求一次函数y=kx+b的表达式；

(2)、若该商场获得利润为W元，试写出利润W与销售单价x之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？

(3)、若该商场获得利润不低于500元，试确定销售单价x的范围．

查看试题解析
23. 如图1，四边形ABCD的对角线AC，BD相交于点O，OA＝OC，OB＝OD+CD．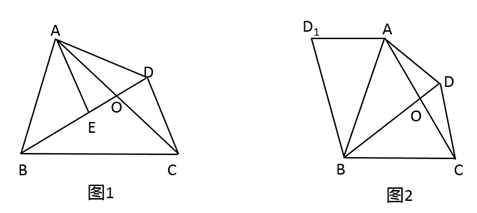

(1)、过点A作AE∥DC交BD于点E，求证：AE＝BE；

(2)、如图2，将△ABD沿AB翻折得到△ABD₁ ．
①求证：BD₁∥CD；

②若AD₁∥BC．求证：CD²＝2OD•BD．

查看试题解析

	频数	频率
体育	40	0.4
科技	25	$a$
艺术	$b$	0.15
其它	20	0.2