安徽省合肥市蜀山区2021年中考数学一模试卷
试卷更新日期:2021-05-08 类型:中考模拟
一、单选题
-
1. 根据《九章算术》记载,中国人最早使用负数,下列负数中最大的是( )A、 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 2021年2月22日,由嫦娥五号从月球带回的月壤样品首次公开亮相,并且即将在中国国家博物馆面向公众展出.已知地球与月球间的平均距离约为38.44万公里,其中38.44万用科学记数法表示为( )A、 B、 C、 D、4. 由长方体和正方体组成的几何体如图水平放置,其俯视图为( )
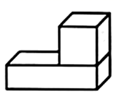 A、
A、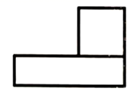 B、
B、 C、
C、 D、
D、 5. 中考体育测试前,某校为了了解选报引体向上的九年级男生的成绩情况,随机抽测了部分九年级男生引体向上的成绩,并将测试的成绩制成了如下的统计表:
5. 中考体育测试前,某校为了了解选报引体向上的九年级男生的成绩情况,随机抽测了部分九年级男生引体向上的成绩,并将测试的成绩制成了如下的统计表:个数
13
14
15
16
人数
3
5
1
1
依据上表提供的信息,下列判断正确的是( )
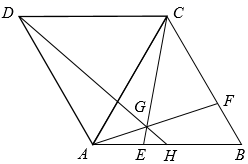
A、众数是5 B、中位数是14.5 C、平均数是14 D、方差是86. 某手机厂商一月份生产手机20万台,计划二、三月份共生产手机45万台,设二、三月平均每月增长率为x,根据题意列出方程为( )A、 B、 C、 D、7. 如图,在四边形 中,请在所给的图形中进行操作:①作点A关于 的对称点P:②作射线 交 于点Q;③连接 .试用所作图形进行判断,下列选项中正确的是( ) A、 B、 C、 D、以上三种情况都有可能8. 一次函数 的图象如图所示,则下列选项中错误的说法是( )
A、 B、 C、 D、以上三种情况都有可能8. 一次函数 的图象如图所示,则下列选项中错误的说法是( )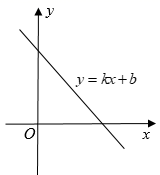 A、 B、当 时, C、若点 与 都在直线 上,则 D、将函数图象向左平移1个单位后,图象恰好经过坐标原点,则9. 如图,在 中, ,E为 中点,连接 , ,若 ,则 的长为( )
A、 B、当 时, C、若点 与 都在直线 上,则 D、将函数图象向左平移1个单位后,图象恰好经过坐标原点,则9. 如图,在 中, ,E为 中点,连接 , ,若 ,则 的长为( ) A、 B、 C、 D、10. 如图是抛物线 的部分图象,其对称轴为直线 且与x轴的一个交点坐标是 ,则下列结论:① ;② ;③ ;④ (m为任意实数).其中正确结论的个数是( )
A、 B、 C、 D、10. 如图是抛物线 的部分图象,其对称轴为直线 且与x轴的一个交点坐标是 ,则下列结论:① ;② ;③ ;④ (m为任意实数).其中正确结论的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 计算: .12. 如图,⊙O经过A,B,C三点, 分别与⊙O相切于点A,C,若 ,点B在优弧 上,则 的度数为 .
 13. 如图,四边形 的面积为6, 在x轴上,且 ,反比例函数 的图象经过四边形的顶点A,则k的值为 .
13. 如图,四边形 的面积为6, 在x轴上,且 ,反比例函数 的图象经过四边形的顶点A,则k的值为 . 14. 如图是一张矩形纸片,点E是 边上一点,将 沿 折叠,使点C落在矩形内的点 处,当点 恰好为矩形对角线中点时,则 ;当点 落在对角线 上,若 共线,且 时,则 的长为 .
14. 如图是一张矩形纸片,点E是 边上一点,将 沿 折叠,使点C落在矩形内的点 处,当点 恰好为矩形对角线中点时,则 ;当点 落在对角线 上,若 共线,且 时,则 的长为 .
三、解答题
-
15. 计算:16. 某校为了“弘扬传统文化,阅读经典名著”,计划给学校图书馆添置书籍,已知《诗经》每本20元,《孟子》每本14元,学校决定购买《诗经》和《孟子》共100本,总费用不超过1790元,那么该学校最多可以购买多少本《诗经》?17. 如图,在边长为1个单位长度的小正方形组成的 的网格中,已知点O,A,B,C均为网格线的交点.
 (1)、将 向右平移4个单位,再向上平移3个单位得到 ,请画出 (点 分别为A,B,C的对应点)(2)、以点O为旋转中心将 逆时针旋转 得到 ,请画出 ;并写出在旋转过程中点 到 所经过的路径长为 . (点 分别为 的对应点)18. 观察与思考:我们知道, ,那么 结果等于多少呢?请你仔细观察,找出下面图形与算式的关系,解决下列问题:
(1)、将 向右平移4个单位,再向上平移3个单位得到 ,请画出 (点 分别为A,B,C的对应点)(2)、以点O为旋转中心将 逆时针旋转 得到 ,请画出 ;并写出在旋转过程中点 到 所经过的路径长为 . (点 分别为 的对应点)18. 观察与思考:我们知道, ,那么 结果等于多少呢?请你仔细观察,找出下面图形与算式的关系,解决下列问题: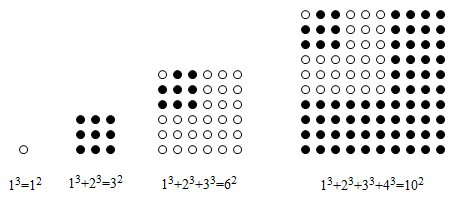
推算:
(1)、 ;(2)、概括: ;(3)、拓展应用:求 的值.19. 如图,某数学兴趣小组要测量某购物广场大楼上安装的显示屏的高度,在点A处测得大楼上显示屏的顶端C点的仰角 为 ,底端D点的仰角 为 ,沿水平地面向前走20米到达E处,测得顶端C的仰角 为 ,点C,D,B在同一条竖直线上,求显示屏的高度 约为多少米?(结果精确到1米)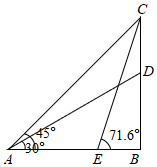
(参考数据: , , , , )
20. 如图, 是半圆O的直径,D是 的中点, 于点E, 交 于点F. (1)、求证: ;(2)、若 ,半圆O的半径为5,求 的长.21. 某校是全国青少年毒品预防教育先进单位,为了让学生掌握禁毒知识,提高防毒意识,组织全校学生参加了“禁毒知识网络答题”活动.该校德育处对全体九年级学生答题成绩进行统计,将成绩分为四个等级:优秀、良好、一般、不合格;根据调査结果绘制了条形统计图和扇形统计图,部分信息如下:
(1)、求证: ;(2)、若 ,半圆O的半径为5,求 的长.21. 某校是全国青少年毒品预防教育先进单位,为了让学生掌握禁毒知识,提高防毒意识,组织全校学生参加了“禁毒知识网络答题”活动.该校德育处对全体九年级学生答题成绩进行统计,将成绩分为四个等级:优秀、良好、一般、不合格;根据调査结果绘制了条形统计图和扇形统计图,部分信息如下: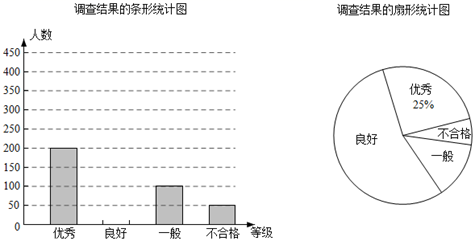 (1)、该校九年级共有名学生,“一般”所占圆心角的度数为 .(2)、已知该市共有16000名学生参加了这次“禁毒知识网络答题”活动,请以该校九年级学生答题成绩统计情况估计,该市大约有多少名学生在这次答题中成绩不合格?(3)、德育处从该校九年级答题成绩前四名(3男1女)学生中随机抽取2名同学参加全市现场禁毒知识竞赛,请用树状图或列表法求出抽到“一男一女”参加的概率.
(1)、该校九年级共有名学生,“一般”所占圆心角的度数为 .(2)、已知该市共有16000名学生参加了这次“禁毒知识网络答题”活动,请以该校九年级学生答题成绩统计情况估计,该市大约有多少名学生在这次答题中成绩不合格?(3)、德育处从该校九年级答题成绩前四名(3男1女)学生中随机抽取2名同学参加全市现场禁毒知识竞赛,请用树状图或列表法求出抽到“一男一女”参加的概率.