安徽省亳州市利辛县2021年中考数学一模试卷

试卷更新日期：2021-05-08 类型：中考模拟

进入出卷网下载

一、单选题

1. 下面的各数中，最小的数是（）

A、2^﹣1 B、 $\sqrt{2}$ C、2 D、﹣（﹣2）

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、（﹣a）³•a⁴＝﹣a⁷ C、（a²）³＝a⁵ D、a⁶÷a²＝a³

查看试题解析
3. 我国中东部地区雾霾天气多发，雾霾中的PM2.5对人体危害极大，PM2.5是指大气中直径小于或等于0.0000000025km可入肺颗粒物，将0.0000000025用科学记数法表示为（）

A、0.25×10^﹣2 B、0.25×10^﹣7 C、2.5×10^﹣9 D、2.5×10^﹣8

查看试题解析
4. 如图所示放置的几何体，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
5. 如图，直线l₁∥ l₂ ， CD⊥AB于点D ，∠1=50°，则∠BCD的度数为（）

A、40° B、45° C、50° D、30°

查看试题解析
6. 不等式组-2≤ $x + 1 < 1$ 的解集，在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
7. 某数学兴趣小组为了了解本班学生一周课外阅读的时间，随机调查5名学生，并将所得数据整理如表：

学生

1

2

3

4

5

一周课外阅读时间（小时）

7

5

4

□

8

表中有一个数字被污染后而模糊不清，但曾计算得该组数据的平均数为6，则这组数据的方差和中位数分别为（）

A、2，6 B、1.5，4 C、2，4 D、6，6

查看试题解析
8. 如图，已知等腰△ABC中，∠ABC＝45°，F是高AD和高BE的交点，AB＝BC＝4，则线段DF的长度为（）

A、2 $\sqrt{2}$ B、2 C、4﹣2 $\sqrt{2}$ D、 $\sqrt{2}$

查看试题解析
9. 已知a≠0，函数y＝ $\frac{- a}{x}$ 与y＝ax²﹣a在同一直角坐标系中的大致图象可能是（）

A、 B、 C、 D、

查看试题解析
10. 如图，在锐角△ABC中，AB＝6，∠ABC＝60°，∠ABC的平分线交AC于点D，点P，Q分别是BD，AB上的动点，则AP＋PQ的最小值为（）

A、6 B、6 $\sqrt{3}$ C、3 D、3 $\sqrt{3}$

查看试题解析

二、填空题

11. 计算 $\frac{1}{x} - \frac{1}{3 x}$ 的结果是.

查看试题解析
12. 分解因式：4x²-100= ．

查看试题解析
13. 如图，正五边形ABCDE的边长为5，分别以点C、D为圆心，CD长为半径画弧，两弧交于点F，则 $\overset{⌢}{B F}$ 的长为．

查看试题解析
14. 如图，在边长为4的正方形ABCD中，P是BC边上一动点（不含B、C两点），将△ABP沿直线AP翻折，点B落在点E处；在CD上有一点M，使得将△CMP沿直线MP翻折后，点C落在直线PE上的点F处，直线PE交CD于点N，连接MA，NA．当△ABP≌△ADN时，则BP的长为．

查看试题解析

三、解答题

15. 计算： $- 1^{4} - | \sqrt{3} - 2 | + 2 \sin 60 ° + \sqrt{9}$ ．

查看试题解析
16. 在抗击新冠肺炎疫情期间，某社区购买酒精和消毒液两种消毒物资，供居民使用．第一次购买酒精和消毒液若干，酒精每瓶10元，消毒液每瓶5元，共花费了350元；第二次又购买了与第一次相同数量的酒精和消毒液，由于酒精和消毒液每瓶价格分别下降了30%和20%，只花费了260元．求每次购买的酒精和消毒液分别是多少瓶？

查看试题解析
17. 如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，△ABC的三个顶点A（5，2）、B（5，5）、C（1，1）均在格点上．
①将△ABC关于x轴对称得到△A₁B₁C₁ ，请画出△A₁B₁C₁_；

②将△ABC绕点O逆时针旋转90°后得到的△A₂B₂C₂ ，画出△A₂B₂C₂并写出点A₂的坐标．

查看试题解析
18. 观察下列各式的规律：
①1×3﹣2²＝3﹣4＝﹣1；

②2×4﹣3²＝8﹣9＝﹣1；

③3×5﹣4²＝15﹣16＝﹣1

…

(1)、请按以上规律写出第④个等式．

(2)、写出第n个等式并证明．

查看试题解析
19. 脱贫攻坚工作让老百姓过上了幸福的生活.如图①是政府给贫困户新建的房屋，如图②是房屋的侧面示意图，它是一个轴对称图形，对称轴是房屋的高 $A B$ 所在的直线.为了测量房屋的高度，在地面上C点测得屋顶 $A$ 的仰角为 $35 °$ ，此时地面上C点、屋檐上 $E$ 点、屋顶上A点三点恰好共线，继续向房屋方向走 $8 m$ 到达点D时，又测得屋檐 $E$ 点的仰角为 $60 °$ ，房屋的顶层横梁 $E F = 12 m$ ， $E F / / C B$ ， $A B$ 交 $E F$ 于点G（点C，D， $B$ 在同一水平线上）.（参考数据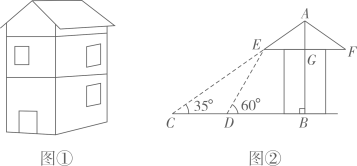： $\sin 35 ° \approx 0.6$ ， $\cos 35 ° \approx 0.8$ ， $\tan 35 ° \approx 0.7$ ， $\sqrt{3} \approx 1.7$ ）

(1)、求屋顶到横梁的距离 $A G$ ；

(2)、求房屋的高 $A B$ （结果精确到 $1 m$ ）.

查看试题解析
20. 已知：如图，AB、AC是⊙O的两条弦，且AB＝AC，D是AO延长线上一点，联结BD并延长交⊙O于点E，联结CD并延长交⊙O于点F.

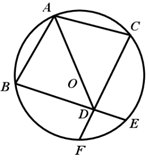(1)、求证：BD＝CD：

(2)、如果AB²＝AO·AD，求证：四边形ABDC是菱形.

查看试题解析

21. 新冠疫情期间，某校开展线上教学，有“录播”和“直播”两种教学方式供学生选择其中一种．为分析该校学生线上学习情况，在接受这两种教学方式的学生中各随机抽取40人调查学习参与度，数据整理结果如表（数据分组包含左端值不包含右端值）．

参与度	0.2～0.4	0.4～0.6	0.6～0.8	0.8～1
录播（人数）	4	16	12	8
直播（人数）	2	10	16	12

(1)、你认为哪种教学方式学生的参与度更高？简要说明理由．

(2)、该校共有800名学生，选择“录播”和“直播”的人数之比为1：3，估计参与度在0.4以下的共有多少人？

(3)、录播参与度在0.2～0.4有三个男生和一个女生，从中任意抽取二位学生，恰好是一男一女的概率是多少？

查看试题解析

22. 在这春暖大地百花将开的季节，安徽省利辛县市民健身公园吸引了不少的游客，一个商家发现了商机，设计了一款成本为10元/件的工艺品进行试销．经过一段时间试营业，得到如下数据：

销售单价x（元/件）	…	20	30	40	50	60	…
每天销售量（y件）	…	50	40	30	20	10	…

(1)、猜想y与x的函数关系，并求出函数关系式；

(2)、利辛县物价部门规定，在不亏本的情况下该工艺品销售单价最高不能超过35元/件，当销售单价定为多少时，该商家试销该工艺品每天获得的利润最大？最大值为多少？

查看试题解析

23. 已知四边形ABCD中，AB＝AD，对角线AC平分∠DAB，点F为AB上一点，且CF＝CB．

(1)、如图1，求证：CD＝CF；

(2)、如图2，连接DF，交AC于点G，求证：△DGC∽△ADC．

(3)、如图3，若点H为线段DG上一点，连接AH，若∠ADC＝2∠HAG，AD＝5，DC＝3，求 $\frac{F G}{G H}$ 的值．

查看试题解析

学生	1	2	3	4	5
一周课外阅读时间（小时）	7	5	4	□	8