云南省曲靖市麒麟区第七中2020-2021学年九年级下学期数学第一次月考试卷
试卷更新日期:2021-05-08 类型:月考试卷
一、填空题
-
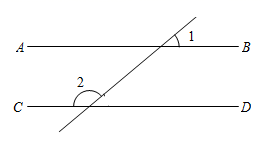
1. 的相反数 .2. 因式分解 .3. 若 有意义,则x的取值范围是 .4. 如图,若 , ,则 度.
 5. 如图,若反比例函数y= (x<0)的图象经过点A , AB⊥x轴于B , 且△AOB的面积为6,则k= .
5. 如图,若反比例函数y= (x<0)的图象经过点A , AB⊥x轴于B , 且△AOB的面积为6,则k= . 6. 在平行四边形 中, 的平分线交直线 于点 ,若 , ,则平行四边形 的周长为 .
6. 在平行四边形 中, 的平分线交直线 于点 ,若 , ,则平行四边形 的周长为 .二、单选题
-
7. 改革开放以来,我国的高等教育得到了极大发展。据有关部门统计, 2020 年全国本科生毕业人数约为874万人。将数8740000用科学记数法表示为( )A、874×104 B、8.74×106 C、8.74×104 D、0.874×1078. 下面的图形既是轴对称图形又是中心对称图形的是( )A、正方形 B、三角形 C、角 D、平行四边形9. 下列运算正确的是( )A、 B、 C、 D、10. 下列立体图形中,主视图是圆的是( )A、
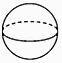 B、
B、 C、
C、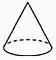 D、
D、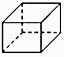 11. 一次函数 与二次函数 在同一平面直角坐标系中的图象可能是( )A、
11. 一次函数 与二次函数 在同一平面直角坐标系中的图象可能是( )A、 B、
B、 C、
C、 D、
D、 12. 如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥底面半径 ,扇形圆心解 ,则该圆锥母线长为( )
12. 如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥底面半径 ,扇形圆心解 ,则该圆锥母线长为( )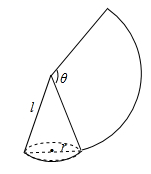 A、10 B、 C、6 D、813. 如图, 为等腰直角三角形,OA1=1,以斜边OA2为直角边作等腰直角三角形OA2A3 , 再以OA3为直角边作等腰直角三角形OA3A4 , …,按此规律作下去,则OAn的长度为( )
A、10 B、 C、6 D、813. 如图, 为等腰直角三角形,OA1=1,以斜边OA2为直角边作等腰直角三角形OA2A3 , 再以OA3为直角边作等腰直角三角形OA3A4 , …,按此规律作下去,则OAn的长度为( ) A、( )n B、( )n﹣1 C、( )n D、( )n﹣114. 如图,在矩形 中, , , 为矩形 对角线的交点,以 为圆心,1为半径作 , 为 上的一个动点,连接 , ,则 面积的最大值是( )
A、( )n B、( )n﹣1 C、( )n D、( )n﹣114. 如图,在矩形 中, , , 为矩形 对角线的交点,以 为圆心,1为半径作 , 为 上的一个动点,连接 , ,则 面积的最大值是( )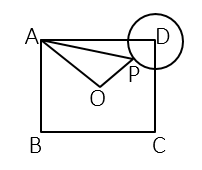 A、 B、 C、 D、
A、 B、 C、 D、三、解答题
-
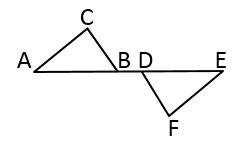
15. 已知:如图,点 , 在线段 上, , , ,求证 .
 16. 若关于 的一元二次方程 有两个不相等的实数根.(1)、求 的取值范围;(2)、若该方程的两个实数根的积为2,求 的值.17. 先化简,再求值: ,其中 时,求原式的值.18. 一只不透明袋子中装有1个白球和2个红球,这些球除颜色外都相同,某课外学习小组做摸球试验:将球搅匀后从中任意摸出1个球,记下颜色后放回、搅匀,不断重复这个过程.(1)、每一次摸到白球的概率为;(2)、现从该袋中摸出2个球,请用树状图或列表的方法列出所有等可能的结果,并求恰好摸到1个白球,1个红球的概率.19. 王大伯承包了一个鱼塘,投放了2000条某种鱼苗,经过一段时间的精心喂养,存活率大致达到了90%.他近期想出售鱼塘里的这种鱼.为了估计鱼塘里这种鱼的总质量,王大伯随机捕捞了20条鱼,分别称得其质量后放回鱼塘.现将这20条鱼的质量作为样本,统计结果如图所示:
16. 若关于 的一元二次方程 有两个不相等的实数根.(1)、求 的取值范围;(2)、若该方程的两个实数根的积为2,求 的值.17. 先化简,再求值: ,其中 时,求原式的值.18. 一只不透明袋子中装有1个白球和2个红球,这些球除颜色外都相同,某课外学习小组做摸球试验:将球搅匀后从中任意摸出1个球,记下颜色后放回、搅匀,不断重复这个过程.(1)、每一次摸到白球的概率为;(2)、现从该袋中摸出2个球,请用树状图或列表的方法列出所有等可能的结果,并求恰好摸到1个白球,1个红球的概率.19. 王大伯承包了一个鱼塘,投放了2000条某种鱼苗,经过一段时间的精心喂养,存活率大致达到了90%.他近期想出售鱼塘里的这种鱼.为了估计鱼塘里这种鱼的总质量,王大伯随机捕捞了20条鱼,分别称得其质量后放回鱼塘.现将这20条鱼的质量作为样本,统计结果如图所示: (1)、这20条鱼质量的中位数是 , 众数是.(2)、求这20条鱼质量的平均数;(3)、经了解,近期市场上这种鱼的售价为每千克18元,请利用这个样本的平均数.估计王大伯近期售完鱼塘里的这种鱼可收入多少元?20. 某市在凤城河风景区举办了端午节赛龙舟活动,小亮在河畔的一幢楼上看到一艘龙舟迎面驶来,他在高出水面 的 处测得在 处的龙舟俯角为 ,他登高 到正上方的 处测得驶至 处的龙舟俯角为 ,问两次观测期间龙舟前进了多少?(结果保留根号)
(1)、这20条鱼质量的中位数是 , 众数是.(2)、求这20条鱼质量的平均数;(3)、经了解,近期市场上这种鱼的售价为每千克18元,请利用这个样本的平均数.估计王大伯近期售完鱼塘里的这种鱼可收入多少元?20. 某市在凤城河风景区举办了端午节赛龙舟活动,小亮在河畔的一幢楼上看到一艘龙舟迎面驶来,他在高出水面 的 处测得在 处的龙舟俯角为 ,他登高 到正上方的 处测得驶至 处的龙舟俯角为 ,问两次观测期间龙舟前进了多少?(结果保留根号)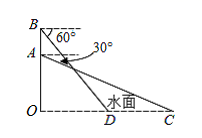 21. 黔东南州某超市购进甲、乙两种商品,已知购进3件甲商品和2件乙商品,需60元;购进2件甲商品和3件乙商品,需65元.(1)、甲、乙两种商品的进货单价分别是多少?(2)、设甲商品的销售单价为x(单位:元/件),在销售过程中发现:当11≤x≤19时,甲商品的日销售量y(单位:件)与销售单价x之间存在一次函数关系,x、y之间的部分数值对应关系如表:
21. 黔东南州某超市购进甲、乙两种商品,已知购进3件甲商品和2件乙商品,需60元;购进2件甲商品和3件乙商品,需65元.(1)、甲、乙两种商品的进货单价分别是多少?(2)、设甲商品的销售单价为x(单位:元/件),在销售过程中发现:当11≤x≤19时,甲商品的日销售量y(单位:件)与销售单价x之间存在一次函数关系,x、y之间的部分数值对应关系如表:销售单价x(元/件)
11
19
日销售量y(件)
18
2
请写出当11≤x≤19时,y与x之间的函数关系式.
(3)、在(2)的条件下,设甲商品的日销售利润为w元,当甲商品的销售单价x(元/件)定为多少时,日销售利润最大?最大利润是多少?22.如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.
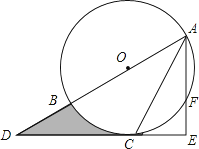 (1)、求证:DE是⊙O的切线;(2)、若AE=6,∠D=30°,求图中阴影部分的面积.23. 如图1,在平面直角坐标系中,抛物线 经过点 和点 ,交 轴于点 .
(1)、求证:DE是⊙O的切线;(2)、若AE=6,∠D=30°,求图中阴影部分的面积.23. 如图1,在平面直角坐标系中,抛物线 经过点 和点 ,交 轴于点 .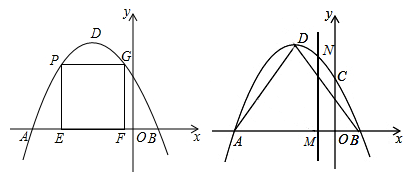 (1)、求抛物线的解析式及顶点 的坐标;(2)、点 是抛物线上 、 之间的一点,过点 作 轴于点 , 轴,交抛物线于点 ,过点 作 轴于点 ,当矩形 的周长最大时,求点 的坐标;(3)、如图2,连接 、 ,点 在线段 上(不与 、 重合),作直线 轴交抛物线于点 ,是否存在点 ,使得 与 相似?若存在,求出点 的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式及顶点 的坐标;(2)、点 是抛物线上 、 之间的一点,过点 作 轴于点 , 轴,交抛物线于点 ,过点 作 轴于点 ,当矩形 的周长最大时,求点 的坐标;(3)、如图2,连接 、 ,点 在线段 上(不与 、 重合),作直线 轴交抛物线于点 ,是否存在点 ,使得 与 相似?若存在,求出点 的坐标;若不存在,请说明理由.