江西省初中名校联盟2020-2021学年九年级下学期数学第一次月考试卷
试卷更新日期:2021-05-08 类型:月考试卷
一、单选题
-
1. 关于 的方程 是一元二次方程,则( )A、 B、 C、 D、2. 下列说法正确的是( )A、某彩票的中奖概率是5%,那么买100张彩票一定有5张中奖 B、某次试验投掷次数是500,计算机记录“钉尖向上”的次数是308,则该次试验“钉尖向上”的频率是0.616 C、当试验次数很大时,概率稳定在频率附近 D、试验得到的频率与概率不可能相等3. 已知反比例函数 ,下列结论错误的是( )A、图象必经过点 B、 随 的增大而增大 C、图象在第二、四象限 D、当 时,4. 小明学习了物理中的杠杆平衡原理发现:阻力 阻力臂 动力 动力臂.现已知某一杠杆的阻力和阻力臂分别为2400N和1m,则动力 (单位:N)关于动力臂 (单位:m)的函数图象大致是( )A、
 B、
B、 C、
C、 D、
D、 5. 如图,在 中, , , 与 交于 ,下列结论:① ;② ;③ ;④ .其中正确结论的个数是( )
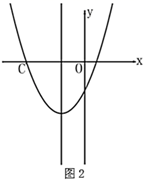
5. 如图,在 中, , , 与 交于 ,下列结论:① ;② ;③ ;④ .其中正确结论的个数是( ) A、1 B、2 C、3 D、46. 抛物线 ( )的对称轴为直线 ,与 轴的一个交点坐标为 ,其部分图象如图所示,下列结论:① ;②方程 的两个根是 , ;③ ;④当 时, 的取值范围是 ;⑤当 时 随 的增大而增大.其中正确结论的个数是( )
A、1 B、2 C、3 D、46. 抛物线 ( )的对称轴为直线 ,与 轴的一个交点坐标为 ,其部分图象如图所示,下列结论:① ;②方程 的两个根是 , ;③ ;④当 时, 的取值范围是 ;⑤当 时 随 的增大而增大.其中正确结论的个数是( )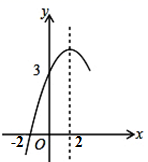 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
7. 已知 ,则 =.8. 某中学校运动会举行 米的班级接力赛,其中九(1)班的甲、乙、丙、丁四位同学随机抽签决定乘一、二、三、四棒,则前两棒是甲、乙两位同学的概率为 .9. 若 , 是一元二次方程 的两个根,则 .10. 如图,为美化校园环境,学校打算在长为30m,宽为20m的长方形空地上修建上一个长方形花圃,并将花圃四周余下的空地修建成宽为 m的通道.若花圃的面积恰好等于264 ,则通道的宽a= m.
 11. 在数学活动课上,老师带领数学小组测量大树 的高度.如图,数学小组发现大树离教学楼有5m,高1.4m的竹竿在水平地面的影子长1m,此时大树的影子有一部分映在地面上,还有一部分映在教学楼的墙上,墙上的影子离 为2m,那么这棵大树高m.
11. 在数学活动课上,老师带领数学小组测量大树 的高度.如图,数学小组发现大树离教学楼有5m,高1.4m的竹竿在水平地面的影子长1m,此时大树的影子有一部分映在地面上,还有一部分映在教学楼的墙上,墙上的影子离 为2m,那么这棵大树高m.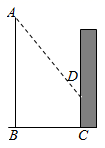 12. 如图,已知直线 , 与 之间的距离为2,在 中, ,点 是直线 上的一个动点, , 中有一边是 的 倍,将 绕点 顺时针旋转 得到 , 所在直线交 于点 ,则 的长度为 .
12. 如图,已知直线 , 与 之间的距离为2,在 中, ,点 是直线 上的一个动点, , 中有一边是 的 倍,将 绕点 顺时针旋转 得到 , 所在直线交 于点 ,则 的长度为 .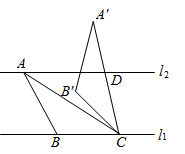
三、解答题
-
13.(1)、解方程: ;(2)、如图,将矩形 绕点 顺时针旋转得到矩形 ,点 的对应点 恰好落在 的延长线上,边 与 相交于点 .

求证: .
14. 已知关于 的方程 .(1)、求证:无论 取何实数,此方程都有两个不相等的实数根;(2)、若方程的两根互为相反数,求 的值.15. 如图已知二次函数 的图象及对称轴,限用无刻度直尺按下列要求作图: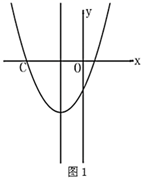
 (1)、在图1中作点 ;(2)、已知 ,在图2中的对称轴上作点P,使 最大;16. 周末,小明进行计算题限时过关训练,现有五张大小、形状和背面样式完全相同的卡片,每张卡片正面各写了一道不同的有理数混合计算的题,其中有两道是有理数简便计算的题.(1)、求小明随机抽取一张卡片为有理数简便计算题的概率;(2)、用树状图法或列表法求小明随机抽取两道题都为有理数简便算法的概率.17. 一个不透明的袋子中有12个红球和若干个白球,在不允许将球倒出来数的前提下,小明采用如下的方法估算其中白球的数量.从袋子中随机摸出一个球,记下颜色,然后把它放回袋子中,摇匀后再随机摸出一个球,记下颜……小明重复上述过程,共摸了200次,其中有120次摸到白球,请回答:(1)、估计袋子中的白球有多少个?(2)、有一个游乐场,要按照上述红球、白球的比例配置彩球池,如果彩球池里共有6000个球,那么需准备多少个红球?18. 某种食品的销售价格 与销售月份 之间的关系如图1所示,成本 与销售月份 之间的关系如图2所示(图1的图象是线段,图2的图象是部分抛物线).
(1)、在图1中作点 ;(2)、已知 ,在图2中的对称轴上作点P,使 最大;16. 周末,小明进行计算题限时过关训练,现有五张大小、形状和背面样式完全相同的卡片,每张卡片正面各写了一道不同的有理数混合计算的题,其中有两道是有理数简便计算的题.(1)、求小明随机抽取一张卡片为有理数简便计算题的概率;(2)、用树状图法或列表法求小明随机抽取两道题都为有理数简便算法的概率.17. 一个不透明的袋子中有12个红球和若干个白球,在不允许将球倒出来数的前提下,小明采用如下的方法估算其中白球的数量.从袋子中随机摸出一个球,记下颜色,然后把它放回袋子中,摇匀后再随机摸出一个球,记下颜……小明重复上述过程,共摸了200次,其中有120次摸到白球,请回答:(1)、估计袋子中的白球有多少个?(2)、有一个游乐场,要按照上述红球、白球的比例配置彩球池,如果彩球池里共有6000个球,那么需准备多少个红球?18. 某种食品的销售价格 与销售月份 之间的关系如图1所示,成本 与销售月份 之间的关系如图2所示(图1的图象是线段,图2的图象是部分抛物线). (1)、已知6月份这种食品的成本最低,求当月出售这种食品每千克的利润(利润 售价 成本)是多少?(2)、求出售这种食品的每千克利润p与销售月份 之间的函数关系式;(3)、哪个月出售这种食品,每千克的利润最大?最大利润是多少?简单说明理由.19. 如图,矩形 的一个顶点与原点重合,两边分别在坐标轴上,反比例函数 的图象与该矩形相交于 , 两点,以这两点为顶点作矩形 ,我们约定这个矩形 为反比例函数 的“相伴矩形”.
(1)、已知6月份这种食品的成本最低,求当月出售这种食品每千克的利润(利润 售价 成本)是多少?(2)、求出售这种食品的每千克利润p与销售月份 之间的函数关系式;(3)、哪个月出售这种食品,每千克的利润最大?最大利润是多少?简单说明理由.19. 如图,矩形 的一个顶点与原点重合,两边分别在坐标轴上,反比例函数 的图象与该矩形相交于 , 两点,以这两点为顶点作矩形 ,我们约定这个矩形 为反比例函数 的“相伴矩形”. (1)、已知点 的坐标为 , .
(1)、已知点 的坐标为 , .①求点 的坐标;
②求证:“相伴矩形” 与原矩形 相似.
(2)、在矩形 中, , ,反比例函数 交 于点 , ,以 为边作矩形 矩形 .求证:矩形 是反比例函数 的“相伴矩形”
20. 两个大小不同且都含有 角的直角三角板按如图所示放置,将 与 的顶点 重合,其中 , .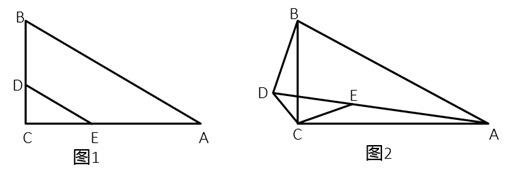 (1)、如图1,当点 在 上,点 在 上时, ,求 ;(2)、如图2,将 绕着点 旋转一定角度时,求 ;(3)、如图2,当点 , , 在同一条直线上时,连接 ,若 , ,求 .21. 如图,已知矩形 的顶点 在反比例函数 的图象上,点 在 轴上,点 在 轴上,点 在反比例函数 的图象上,其横坐标为 ,过点 作 轴于点 , 轴于点 ,交 于点 .
(1)、如图1,当点 在 上,点 在 上时, ,求 ;(2)、如图2,将 绕着点 旋转一定角度时,求 ;(3)、如图2,当点 , , 在同一条直线上时,连接 ,若 , ,求 .21. 如图,已知矩形 的顶点 在反比例函数 的图象上,点 在 轴上,点 在 轴上,点 在反比例函数 的图象上,其横坐标为 ,过点 作 轴于点 , 轴于点 ,交 于点 . (1)、求反比例函数的解析式;(2)、若四边形 为正方形,求点 的坐标;(3)、连接 交 于点 ,若 ,求四边形 与四边形 的面积比.22. 如图1,已知 ,四根长度相等的木棒, , , , 首尾相接组成四边形 ,点 是 的中点,连接 , 交于点 , 的垂直平分线 交 于点 ,交 于点 ,连接 .
(1)、求反比例函数的解析式;(2)、若四边形 为正方形,求点 的坐标;(3)、连接 交 于点 ,若 ,求四边形 与四边形 的面积比.22. 如图1,已知 ,四根长度相等的木棒, , , , 首尾相接组成四边形 ,点 是 的中点,连接 , 交于点 , 的垂直平分线 交 于点 ,交 于点 ,连接 . (1)、求证: ;(2)、如图2,若 ,求证:四边形 是正方形;(3)、将木棒 固定在射线 上,当木棒 绕着点 由 开始顺时针旋转时,四边形 也随之发生变化,设 ,且 满足 .若 是直角三角形,请直接写出 的值.23. 如图,已知二次函数 : ,其中 为正整数,它与 轴相交于点 .
(1)、求证: ;(2)、如图2,若 ,求证:四边形 是正方形;(3)、将木棒 固定在射线 上,当木棒 绕着点 由 开始顺时针旋转时,四边形 也随之发生变化,设 ,且 满足 .若 是直角三角形,请直接写出 的值.23. 如图,已知二次函数 : ,其中 为正整数,它与 轴相交于点 .
 (1)、求二次函数 的最小值(用含 的代数式表示).(2)、将二次函数 向左平移 个单位得到二次函数 .
(1)、求二次函数 的最小值(用含 的代数式表示).(2)、将二次函数 向左平移 个单位得到二次函数 .①若二次函数 与二次函数 关于 轴对称,求 的值;
②二次函数 顶点的纵坐标 与横坐标 之间存在一个函数关系,求这个函数关系式.
(3)、在二次函数 中,当 依次取1,2,3,…, 时,抛物线依次交直线 于点 , , ,…, ,顶点依次为 , , ,…, .①连接 , , , ,求证: ;
②求 的值.