河北省邢台市2020-2021学年九年级下学期数学3月月考试卷
试卷更新日期:2021-05-08 类型:月考试卷
一、单选题
-
1. 如图,有两种说法:①线段 的长是点 到点 的距离;②线段 的长是直线 、 之间的距离关于这两种说法,正确的是( )
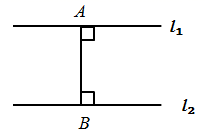 A、①正确,②错误 B、①正确,②正确 C、①错误,②正确 D、①错误,②错误2. 如图,在数轴上,注明了四段的范围,若某段上有两个整数,则这段是( )
A、①正确,②错误 B、①正确,②正确 C、①错误,②正确 D、①错误,②错误2. 如图,在数轴上,注明了四段的范围,若某段上有两个整数,则这段是( )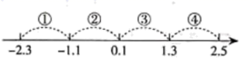 A、段① B、段② C、段③ D、段④3. 若 用科学记数法表示为 ,则n的值是( )A、9 B、10 C、11 D、124. 如图是 的网格图,将图中标有①、②、③、④的一个小正方形涂灰,使所有的灰色图形构成中心对称图形,则涂灰的小正方形是( )
A、段① B、段② C、段③ D、段④3. 若 用科学记数法表示为 ,则n的值是( )A、9 B、10 C、11 D、124. 如图是 的网格图,将图中标有①、②、③、④的一个小正方形涂灰,使所有的灰色图形构成中心对称图形,则涂灰的小正方形是( )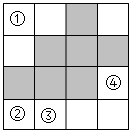 A、① B、② C、③ D、④5. 在一个不透明的口袋中,放入五个完全相同的小球,每个小球上分别标有数字“1”、“2”、“3”、“4”、“5”中的一个(不允许重复),从口袋里同时摸出两个小球,则下列事件是随机事件的是( )A、两个小球上数字之和等于1 B、两个小球上数字之和大于1 C、两个小球上数字之和等于9 D、两个小球上数字之和大于96. 若把 , 的值同时扩大为原来的2倍,则下列分式的值保持不变的是( )A、 B、 C、 D、7. 如图,若 与 是位似图形,则位似中心可能是( )
A、① B、② C、③ D、④5. 在一个不透明的口袋中,放入五个完全相同的小球,每个小球上分别标有数字“1”、“2”、“3”、“4”、“5”中的一个(不允许重复),从口袋里同时摸出两个小球,则下列事件是随机事件的是( )A、两个小球上数字之和等于1 B、两个小球上数字之和大于1 C、两个小球上数字之和等于9 D、两个小球上数字之和大于96. 若把 , 的值同时扩大为原来的2倍,则下列分式的值保持不变的是( )A、 B、 C、 D、7. 如图,若 与 是位似图形,则位似中心可能是( ) A、 B、 C、 D、8. 方程 的解为( )A、 B、 C、 , D、 ,9. 如图,已知点 、点 是同一幢楼上的两个不同位置,从 点观测标志物 的俯角是65°,从 点观测标志物 的俯角是35°,则 的度数为( )
A、 B、 C、 D、8. 方程 的解为( )A、 B、 C、 , D、 ,9. 如图,已知点 、点 是同一幢楼上的两个不同位置,从 点观测标志物 的俯角是65°,从 点观测标志物 的俯角是35°,则 的度数为( )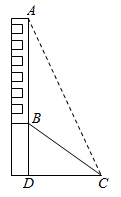 A、25° B、30° C、35° D、65°10. 若 ,则 的值是( )A、100 B、199 C、200 D、29911. 证明:平行四边形的对角线互相平分
A、25° B、30° C、35° D、65°10. 若 ,则 的值是( )A、100 B、199 C、200 D、29911. 证明:平行四边形的对角线互相平分已知:如图,四边形 是平行四边形,对角线 , 相交于点
求证: ,
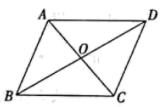
证明:∵四边形 是平行四边形,
∴……………………
∴ , ,
∴ ,
∴ ,
其中,在“四边形 是平行四边形”与“ , ”之间应补充的步骤是( )
A、 , B、 , C、 , D、 ,12. 把如图所示的正方形展开,得到的平面展开图可以是( )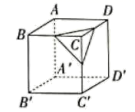 A、
A、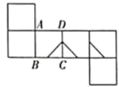 B、
B、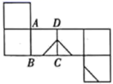 C、
C、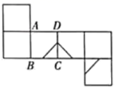 D、
D、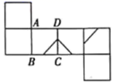 13. 船工小王驾驶一艘小艇匀速从甲港向乙港航行,离开甲港后不久便发现有重要物品落在甲港,小王马上驾驶小艇以相同的速度驰回甲港,到达甲港后,因找重要物品耽误了一段时间,为了按时到达乙港,小王回乙港时,加快了航行速度.则小艇离乙港的距离y与时间t之间的函数关系的大致图象是( )A、
13. 船工小王驾驶一艘小艇匀速从甲港向乙港航行,离开甲港后不久便发现有重要物品落在甲港,小王马上驾驶小艇以相同的速度驰回甲港,到达甲港后,因找重要物品耽误了一段时间,为了按时到达乙港,小王回乙港时,加快了航行速度.则小艇离乙港的距离y与时间t之间的函数关系的大致图象是( )A、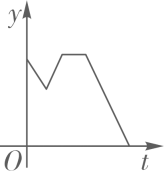 B、
B、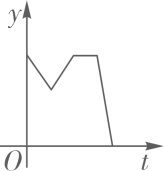 C、
C、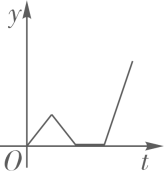 D、
D、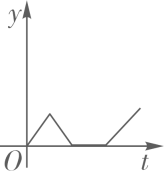 14. 如图,在 中,作以 为内角,四个顶点都在 边上的菱形时,如下的作图步骤是打乱的.
14. 如图,在 中,作以 为内角,四个顶点都在 边上的菱形时,如下的作图步骤是打乱的.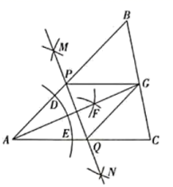
①分别以点 , 为圆心,大于 的长为半径在 的两侧作弧,两弧相交于点 , ;
②作直线 分别交 , 于点 , ,连接 , ;
③分别以点 , 为圆心,大于 的长为半径作弧,两弧相交于 内一点 ,连接 并延长交边 于点 ;
④以点 为圆心,小于 长为半径作弧,分别交 , 于点 , .
则正确的作图步骤是( )
A、②④①③ B、④③②① C、②④③① D、④③①②15. 嘉淇用一些完全相同的 纸片,已知六个 纸片按照图1所示的方法拼接可得外轮廓是正六边形图案,若用 个 纸片按图2所示的方法拼接,那么可以得到外轮廓的图案是( )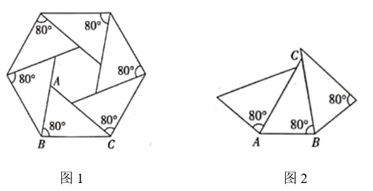 A、正十二边形 B、正十边形 C、正九边形 D、正八边形16. 对于题目:“已知 , ,抛物线 与线段 (包含端点 、 )只有一个公共点,求 的取值范围”.甲的结果是 ,乙的结果是 ,则( )A、甲的结果正确 B、乙的结果正确 C、甲、乙的结果合在一起才正确 D、甲、乙的结果合在一起也不正确
A、正十二边形 B、正十边形 C、正九边形 D、正八边形16. 对于题目:“已知 , ,抛物线 与线段 (包含端点 、 )只有一个公共点,求 的取值范围”.甲的结果是 ,乙的结果是 ,则( )A、甲的结果正确 B、乙的结果正确 C、甲、乙的结果合在一起才正确 D、甲、乙的结果合在一起也不正确二、填空题
-
17. 计算 .18. 如图, 沿 平到 , 交 于点 ,若 , 是 的中点,则 .
 19. 如图1,有一个足够长的矩形纸片 , 、 分别是 、 上的点, .
19. 如图1,有一个足够长的矩形纸片 , 、 分别是 、 上的点, .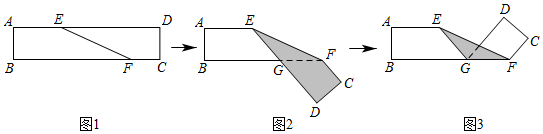 (1)、将纸片含 的部分沿 折叠,称为第1次操作;如图2,则 ;(2)、继续将纸片含 的部分沿 折叠,称为第2次操作;如图3,则 ;以后,重复上述这两步操作,分别记作第3次,第4次,第5次……第n操作,则n的最大值为 .
(1)、将纸片含 的部分沿 折叠,称为第1次操作;如图2,则 ;(2)、继续将纸片含 的部分沿 折叠,称为第2次操作;如图3,则 ;以后,重复上述这两步操作,分别记作第3次,第4次,第5次……第n操作,则n的最大值为 .三、解答题
-
20. 利用运算律计算有时可以简便
例1: ;
例2: .
请你参考黑板中老师的讲解,用运算律简便计算.
(1)、 ;(2)、计算: .21. 已知两个整式 , ,其中系数
,其中系数  被污染. (1)、若
被污染. (1)、若 是 ,化简 ; (2)、若 时, 的值为18
是 ,化简 ; (2)、若 时, 的值为18①说明原题中
 是几?
是几?②若再添加一个常数 ,使 , , 的和不为负数,求 的最小值.
22. 在中考理化实验操作中,初三某班除两名同学因故外全部参加考试,考试结束后,把得到的成绩(均为整数分,满分10分)进行统计并制成如图1所示的条形统计图和如图2所示的扇形统计图(不完整).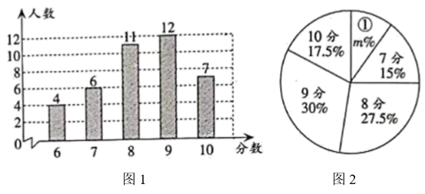 (1)、 ;(2)、若从这些同学中,随机抽取一名整理一下实验器材,求恰好抽到成绩不小于8分同学的概率;(3)、若两名同学经过补测,把得到的成绩与原来成绩合并后,发现成绩的中位数发生改变,求这两名同学的成绩和.23. 如图,已知正方形 ,点 在对角线 上,过点 作 交边 于点 (点 不与 、 重合),延长 至点 ,使得 ,连接 .
(1)、 ;(2)、若从这些同学中,随机抽取一名整理一下实验器材,求恰好抽到成绩不小于8分同学的概率;(3)、若两名同学经过补测,把得到的成绩与原来成绩合并后,发现成绩的中位数发生改变,求这两名同学的成绩和.23. 如图,已知正方形 ,点 在对角线 上,过点 作 交边 于点 (点 不与 、 重合),延长 至点 ,使得 ,连接 .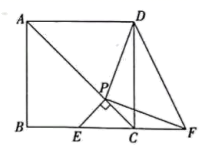 (1)、求证: ;(2)、若 ,求 的度数;(3)、若点 是 的内心,连接 、 直接写出 的取值范围.24. 如图,已知直线 ,经过点 、点 ,交 轴于点 ,点 是 轴上一个动点,过点 、 作直线 .
(1)、求证: ;(2)、若 ,求 的度数;(3)、若点 是 的内心,连接 、 直接写出 的取值范围.24. 如图,已知直线 ,经过点 、点 ,交 轴于点 ,点 是 轴上一个动点,过点 、 作直线 .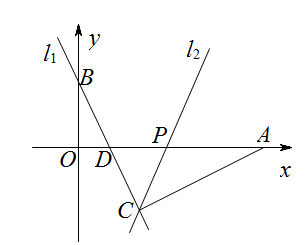 (1)、求直线 的表达式;(2)、已知点 ,当 时,求点 的坐标;(3)、设点 的横坐标为 ,点 , 是直线 上任意两个点,若 时,有 ,请直接写出 的取值范围.25. 如图1,在 中, , , , 是 的中点,以点 为圆心在 的右侧作半径为3的半圆 ,分别交 于点 、 ,交 于点 、 .
(1)、求直线 的表达式;(2)、已知点 ,当 时,求点 的坐标;(3)、设点 的横坐标为 ,点 , 是直线 上任意两个点,若 时,有 ,请直接写出 的取值范围.25. 如图1,在 中, , , , 是 的中点,以点 为圆心在 的右侧作半径为3的半圆 ,分别交 于点 、 ,交 于点 、 .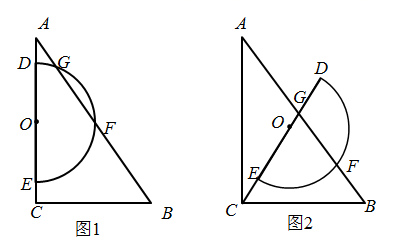 (1)、连接 ,若 ,求 的长度;(2)、如图2,将线段 连同半圆 绕点 旋转.
(1)、连接 ,若 ,求 的长度;(2)、如图2,将线段 连同半圆 绕点 旋转.①在旋转过程中,求点 到 距离的最小值;
②若半圆 与 的直角边相切,设切点为 ,连接 ,求 的长.
26. 在新型冠状肺炎疫情期间,某农业合作社决定对一种特色水果开展线上销售,考虑到实际情况,一共开展了30次线上销售,综合考虑各种因素,该种水果的成本价为每吨2万元,销售结束后,经过统计得到了如下信息:信息1:设第 次线上销售水果 (吨),且第一次线上销售水果为39吨,然后每一次总比前一次销售减少1吨;
信息2:该水果的销售单价 (万元/吨)均由基本价和浮动价两部分组成,其中基本价保持不变,第1次线上销售至第15次线上销售的浮动价与销售场次 成正比,第16次线上销售至第30次线上销售的浮动价与销售场次 成反比;
信息3:
(次)
2
8
24
(万元)
2.2
2.8
3
请根据以上信息,解决下列问题.
(1)、求 与 之间的函数关系式;(2)、若 (万元/吨),求 的值;(3)、在这30次线上销售中,哪一次线上销售获得利润最大?最大利润是多少?