山东省德州市庆云县八校2020-2021学年九年级下学期数学4月月考试卷
试卷更新日期:2021-05-08 类型:月考试卷
一、单选题
-
1. 下列计算正确的是( )A、﹣(﹣3)2=9 B、 =3 C、﹣(﹣2)0=1 D、|﹣3|=﹣32. 下列银行标志中,既不是中心对称图形也不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 甲是某零件的直观图,则它的主视图为( )
3. 甲是某零件的直观图,则它的主视图为( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 第六次全国人口普查数据显示,德州市常驻人口约为556.82万人,此数用科学记数法表示正确的是( )A、556.82×104 B、5.5682×102 C、5.5682×106 D、5.5682×1055. 如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为( )
4. 第六次全国人口普查数据显示,德州市常驻人口约为556.82万人,此数用科学记数法表示正确的是( )A、556.82×104 B、5.5682×102 C、5.5682×106 D、5.5682×1055. 如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为( ) A、30° B、60° C、80° D、120°6. 不等式组 的解集在数轴上可表示为( )A、
A、30° B、60° C、80° D、120°6. 不等式组 的解集在数轴上可表示为( )A、 B、
B、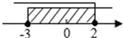 C、
C、 D、
D、 7. 如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1:2,则斜坡AB的长为( )米
7. 如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1:2,则斜坡AB的长为( )米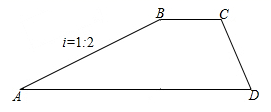 A、 B、 C、 D、248. 如图反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法错误的是( )
A、 B、 C、 D、248. 如图反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法错误的是( ) A、体育场离张强家2.5千米 B、张强在体育场锻炼了15分钟 C、体育场离早餐店4千米 D、张强从早餐店回家的平均速度是3千米/小时9. 雷霆队的杜兰特当选为2013﹣2014赛季NBA常规赛MVP,下表是他8场比赛的得分,则这8场比赛得分的众数与中位数分别为( )
A、体育场离张强家2.5千米 B、张强在体育场锻炼了15分钟 C、体育场离早餐店4千米 D、张强从早餐店回家的平均速度是3千米/小时9. 雷霆队的杜兰特当选为2013﹣2014赛季NBA常规赛MVP,下表是他8场比赛的得分,则这8场比赛得分的众数与中位数分别为( )场次
1
2
3
4
5
6
7
8
得分
30
28
28
38
23
26
39
42
A、29,28 B、28,29 C、28,28 D、28,2710. 下列命题中,真命题是( )A、若a>b,则c﹣a<c﹣b B、某种彩票中奖的概率是1%,买100张该种彩票一定会中奖 C、点M(x1 , y1),点N(x2 , y2)都在反比例函数y= 的图象上,若x1<x2 , 则y1>y2 D、甲、乙两射击运动员分别射击10次,他们射击成绩的方差分别为 =4, =9,这过程中乙发挥比甲更稳定11. 分式方程 的解是( )A、x=1 B、x=﹣1+ C、x=2 D、无解12. 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2 .
以上结论中,你认为正确的有( )个.
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 计算: = .14. 若 ,则(x+y)y= .15. 方程3x(x-1)=2(x-1)的根是16. 如图,正三角形ABC的边长为2,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心,半径为1作圆,则圆中阴影部分的面积是 .
 17. 方程x2+2kx+k2﹣2k+1=0的两个实数根x1 , x2满足x12+x22=4,则k的值为 .18. 如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1、A2、A3…An , ….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1、M2、M3、…Mn , …都在直线L:y=x上;②抛物线依次经过点A1、A2、A3…An、….则顶点M2014的坐标为 .
17. 方程x2+2kx+k2﹣2k+1=0的两个实数根x1 , x2满足x12+x22=4,则k的值为 .18. 如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1、A2、A3…An , ….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1、M2、M3、…Mn , …都在直线L:y=x上;②抛物线依次经过点A1、A2、A3…An、….则顶点M2014的坐标为 .
三、解答题
-
19. 先化简,再求值: ﹣1,其中a=2sin60°﹣tan45°,b=1.20. 2011年5月,我市某中学举行了“中国梦•校园好少年”演讲比赛活动,根据学生的成绩划分为A,B,C,D四个等级,并绘制了不完整的两种统计图.

根据图中提供的信息,回答下列问题:
(1)、参加演讲比赛的学生共有人,并把条形图补充完整;(2)、扇形统计图中,m= , n=;C等级对应扇形的圆心角为度;(3)、学校欲从获A等级的学生中随机选取2人,参加市举办的演讲比赛,请利用列表法或树状图法,求获A等级的小明参加市比赛的概率.21. 目前节能灯在城市已基本普及,今年全省面向县级及农村地区推广,为响应号召,某商场计划购进甲,乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:进价(元/只)
售价(元/只)
甲型
25
30
乙型
45
60
(1)、如何进货,进货款恰好为46000元?(2)、如何进货,商场销售完节能灯时获利最多且不超过进货价的30%,此时最大利润为多少元?22. 如图,双曲线y= (x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3). (1)、确定k的值;(2)、若点D(3,m)在双曲线上,求直线AD的解析式;(3)、计算△OAB的面积.23.
(1)、确定k的值;(2)、若点D(3,m)在双曲线上,求直线AD的解析式;(3)、计算△OAB的面积.23.如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.
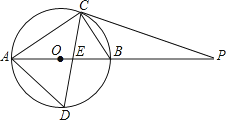 (1)、求AC、AD的长;(2)、试判断直线PC与⊙O的位置关系,并说明理由.
(1)、求AC、AD的长;(2)、试判断直线PC与⊙O的位置关系,并说明理由.
24.(1)、问题背景如图1:在四边形ABCD中,AB=AD, BAD=120°, B= ADC=90°.E,F 分别是 BC,CD上的点.且 EAF=60°.探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG.先证明ΔABE≌ΔADG;再证明ΔAEF≌ΔAGF,可得出结论,他的结论应是 ;
请你帮他完成证明过程
 (2)、探索延伸:
(2)、探索延伸:如图2,若在四边形ABCD中,AB=AD, B+ D=180°.E,F分别是BC,CD上的点,且 EAF= BAD,上述结论是否仍然成立,并说明理由;
(3)、实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(0处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲,乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
25. 如图,在平面直角坐标系中,已知点B的坐标是(﹣1,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.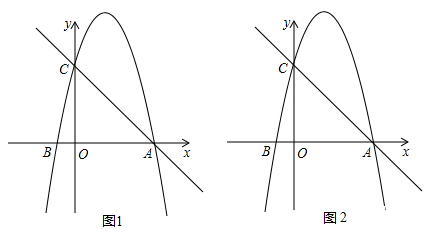 (1)、求抛物线的解析式;(2)、是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;(3)、过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,写出点P的坐标(不要求写解题过程).
(1)、求抛物线的解析式;(2)、是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;(3)、过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,写出点P的坐标(不要求写解题过程).