河北省唐山市滦州市2020-2021学年八年级下学期数学第一次月考试卷

试卷更新日期：2021-05-08 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列图案中，既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各点中，位于第四象限的点是（）

A、(3,-4) B、(3,4) C、(-3,4) D、(-3,-4)

查看试题解析
3. 如果分式 $\frac{| x | - 1}{x + 1}$ 的值为0，那么 $x$ 的值为（）

A、-1 B、1 C、-1或1 D、1或0

查看试题解析
4. 下列运算正确的是（）

A、 $\sqrt{2}$ + $\sqrt{3}$ = $\sqrt{5}$ B、 $\sqrt{18}$ =2 $\sqrt{3}$ C、 $\sqrt{2}$ • $\sqrt{3}$ = $\sqrt{5}$ D、 $\sqrt{2}$ ÷ $\sqrt{\frac{1}{2}}$ =2

查看试题解析
5. 如图，∠ACB＝90°，AC＝BC，AD⊥CE，BE⊥CE，垂足分别是点D、E，AD＝3，BE＝1，则DE的长是（）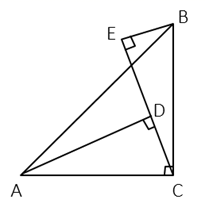

A、2 B、4 C、2 $\sqrt{2}$ D、 $\sqrt{10}$

查看试题解析
6. 将一个长为2，宽为1的长方形ABCD按如图方式放在数轴上，使点A与原点O重合，若以O为圆心，以AC的长为半径画圆，则这个圆与数轴的交点所表示的数是（）

A、 $\sqrt{5}$ B、﹣ $\sqrt{5}$ C、± $\sqrt{5}$ D、±2.5

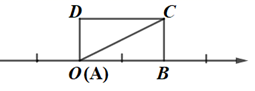查看试题解析
7. 如图，在△ABC中，AC的垂直平分线分别交AC、BC于E，D两点，EC＝4，△ABC的周长为23，则△ABD的周长为（）

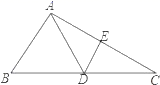A、13 B、15 C、17 D、19

查看试题解析
8. 已知 $\frac{1}{x} - \frac{1}{y}$ =3，则代数式 $\frac{2 x + 3 x y - 2 y}{x - x y - y}$ 的值是（）

A、 $- \frac{7}{2}$ B、 $- \frac{11}{2}$ C、 $\frac{9}{2}$ D、 $\frac{3}{4}$

查看试题解析
9. 如图，在△ABC中，CD⊥AB于点D，BE⊥AC于点E，F为BC的中点，DE=5，BC=8，则△DEF的周长是（）

A、21 B、18 C、15 D、13

查看试题解析
10. 如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，BM，下面的结论：①△ABE≌△DBC；②∠DMA=60°；③△BPQ为等边三角形；④MB平分∠AMC，其中结论正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 化简： $| \sqrt{3} - 2 |$ = ．

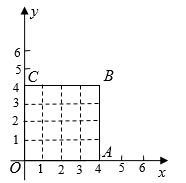
查看试题解析
12. 已知一个边长为4的正方形OABC，按如图所示的方式放在平面直角坐标系中，其中的一个顶点与原点重合，两边分别与x轴、y轴重合．则顶点A的坐标是．

查看试题解析
13. 如图，已知 $∠ A B C = ∠ D C B$ ，添加下列条件中的一个：① $∠ A = ∠ D$ ，② $A C = D B$ ，③ $A B = D C$ ，其中不能确定 $Δ A B C$ ≌△ $Δ D C B$ 的是（只填序号）.

查看试题解析
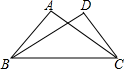14. 如图， $△ A B C$ 中，∠C＝90°，AC＝BC，AD平分∠BAC交BC于点D，DE⊥AB，垂足为E，且AB＝10cm，则 $△ D E B$ 的周长是cm.

查看试题解析
15. 若y＝ $\sqrt{x - 3}$ + $\sqrt{3 - x}$ ﹣2，则 $\sqrt{x + y}$ 的值是．

查看试题解析
16. 如图所示，在△ABC中，OB，OC分别是∠ABC和∠ACB的平分线，过点O的直线MN∥BC，交AB，AC于M，N，若MN＝6cm，则BM+CN＝cm．

查看试题解析
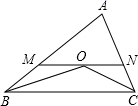17. 如下图，在四边形ABCD中， $AB = 4 cm$ ， $BC = 3 cm$ ， $CD = 12 cm$ ， $DA = 13 cm$ ，且 $∠ ABC = 90 °$ ，则四边形ABCD的面积为．

查看试题解析
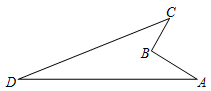18. 已知a＝3+2 $\sqrt{2}$ ，b＝3﹣2 $\sqrt{2}$ ，则a²b﹣ab²＝．

查看试题解析
19. 若一个等腰三角形的底角为15°，腰长为8，则这个等腰三角形的面积是．

查看试题解析
20. 已知：如图，AD是等边△ABC中∠BAC的平分线，P是AD上一点，E为AC中点，连接PC，PE，若AB＝6，则PC+PE的最小值是．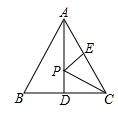

查看试题解析

三、解答题

21. 计算： $(\sqrt{48} + \sqrt{27} - \sqrt{12}) \div \sqrt{6}$ ．

查看试题解析
22. 已知：如图，AD平分∠BAC，DE⊥AB，DF⊥AC，垂足分别为E，F，且∠ABD+∠ACD＝180°．
求证：BD＝CD．

查看试题解析
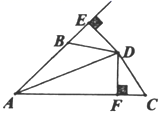23. 在我市“青山绿水”行动中，某社区计划对面积为3600m²的区域进行绿化，经投标由甲、乙两个工程队来完成．已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍，如果两队各自独立完成面积为600m²区域的绿化时，甲队比乙队少用6天．求甲，乙两工程队每天各能完成多少面积的绿化？

查看试题解析
24. 已知：如图，△ABC是等边三角形，D，E分别是BC，AC上的点，且AE＝CD，AD，BE交于点P，BQ⊥AD于点Q．

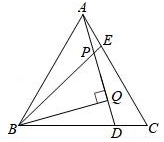(1)、求证：∠ABE＝∠CAD．

(2)、若PQ＝3，PE＝1，求BE的长．

查看试题解析
25. 阂读材料，回答问题：
观察下列各式：

$\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}}$ ＝1+ $\frac{1}{1}$ ﹣ $\frac{1}{2}$ ＝1 $\frac{1}{2}$ ；

$\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}}$ ＝1+ $\frac{1}{2}$ ﹣ $\frac{1}{3}$ ＝1 $\frac{1}{6}$ ；

$\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}}$ ＝1+ $\frac{1}{3}$ ﹣ $\frac{1}{4}$ ＝1 $\frac{1}{12}$ ．

请你根据以上三个等式提供的信息解答下列问题：

(1)、猜想： $\sqrt{1 + \frac{1}{6^{2}} + \frac{1}{7^{2}}}$ ＝＝；

(2)、归纳：根据你的观察、猜想，写出一个用n．（n为正整数）表示的等式：；

(3)、应用：用上述规律计算 $\sqrt{\frac{82}{81} + \frac{1}{100}}$ ．

查看试题解析
26. 已知△ABC中，∠BAC＝90°，AB＝AC，点D为直线BC上的一动点（点D不与点B、C重合），以AD为边作△ADE，使∠DAE＝90°，AD＝AE，连接CE．

(1)、如图1，当点D在边BC上时，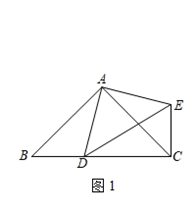

请写出BD和CE之间的位置关系为，并猜想BC和CE、CD之间的数量关系：．

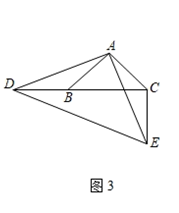
(2)、如图2，当点D在边BC的延长线上且其他条件不变时，（1）中BD和CE之间的位置关系，BC和CE、CD之间的数量关系是否成立？若成立，请证明；若不成立，请写出新的数量关系，说明理由；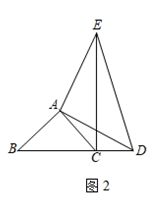

(3)、如图3，当点D在边CB的延长线上且其他条件不变时，若BC＝7，CE＝5，直接写出线段ED的长．

查看试题解析