河南省驻马店市平舆县2019-2020学年八年级下学期数学期中考试试卷

试卷更新日期：2021-05-08 类型：期中考试

进入出卷网下载

一、单选题

1. 已知 $\sqrt{{(2 - x)}^{2}}$ ＝ $x - 2$ ，则 $x$ 的取值范围是（）

A、 $x \leq 2$ B、 $x < 2$ C、 $x > 2$ D、 $x \geq 2$

查看试题解析
2. 化简二次根式 $\sqrt{{(- 5)}^{2} \times 3}$ 的值为（）

A、 $- 5 \sqrt{3}$ B、 $5 \sqrt{3}$ C、 $\pm 5 \sqrt{3}$ D、 $\sqrt{75}$

查看试题解析
3. 如图，在▱ABCD中，∠ODA=90°，AC=10cm，BD=6cm，则BC的长为（）

A、4cm B、5cm C、6cm D、8cm

查看试题解析
4. 下列二次根式的运算：① $\sqrt{2} \times \sqrt{3} = 2 \sqrt{3}$ ；② $\sqrt{18} - \sqrt{8} = \sqrt{2}$ ；③ $\frac{2}{\sqrt{5}} = \frac{2 \sqrt{5}}{5}$ ；④ $\sqrt{{(- 2)}^{2}} = - 2$ ；其中运算正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 已知 $a 、 b 、 c$ 是三角形的三边长，如果满足 ${(a - 1)}^{2} + \sqrt{b - 2} + | c - \sqrt{3} | = 0$ ，则三角形的形状是（）

A、等腰三角形 B、等边三角形 C、直角三角形 D、钝角三角形

查看试题解析
6. 下面二次根式中,是最简二次根式的是（）

A、 $\sqrt{24}$ B、 $\sqrt{0.5}$ C、 $\sqrt{a^{2} + 4}$ D、 $\sqrt{\frac{a}{b}}$

查看试题解析
7. 为比较 $\sqrt{13} + \sqrt{6}$ 与 $\sqrt{13 + 6}$ 的大小，小亮进行了如下分析后作一个直角三角形，使其两直角边的长分别为 $\sqrt{13}$ 与 $\sqrt{6}$ ，则由的股定理可求得其斜边长为 $\sqrt{{(\sqrt{13})}^{2} + {(\sqrt{6})}^{2}} = \sqrt{13 + 6}$ .根据“三角形三边关系”，可得 $\sqrt{13} + \sqrt{6} > \sqrt{13 + 6}$ .小亮的这一做法体现的数学思想是（）

A、分类讨论思想 B、方程思想 C、类比思想 D、数形结合思想

查看试题解析
8. 正方形具有而菱形不具有的性质是（）

A、对角线垂直且互相平分 B、每一条对角线平分一组对角 C、对角线相等 D、对边相等

查看试题解析
9. 如图，在四边形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点 $O$ ，且 $O A = O C$ ， $O B = O D$ ，下列结论不一定成立的是（）

A、 $A D = B C$ B、 $A B // C D$ C、 $∠ D A B = ∠ B C D$ D、 $∠ D A B = ∠ A B C$

查看试题解析
10. 如图，2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的《勾股圆方图》（也称《赵爽弦图》），它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形，如图所示，如果大正方形的面积是13，小正方形的面积是1，直角三角形的短直角边为a，较长直角边为b，那么 $（ a + b ）^{2}$ 的值为（）

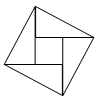A、13 B、19 C、25 D、169

查看试题解析

二、填空题

11. “矩形的对角线相等”的逆命题为，该逆命题是命题（真、假）

查看试题解析
12. 已知线段a=3，b=4，若线段c能和a，b构成直角三角形，则c的长度是.

查看试题解析
13. 在菱形ABCD中,对角线AC=30，BD=60，则菱形ABCD的面积为．

查看试题解析
14. 如图，在平行四边形 $A B C D$ 中， $D B = D C$ ， $∠ A = 65 °$ ， $C E ⊥ B D$ 于 $E$ ，则 $∠ B C E =$ ．

查看试题解析
15. 如图，将矩形ABCD折叠，折痕为EF，BC的对应边B'C′与CD交于点M，若∠B′MD=50°，则∠BEF的度数为.

查看试题解析

三、解答题

16. 计算

(1)、 $\sqrt{18} + \sqrt{\frac{9}{2}} + {(\sqrt{3} - 2)}^{0} + \sqrt{{(1 - \sqrt{2})}^{2}}$

(2)、 ${(\sqrt{2} + \sqrt{3})}^{2} (5 - 2 \sqrt{6})$

查看试题解析
17. 计算：

(1)、已知 $x = 2 - \sqrt{3}$ ，求代数式 $x^{2} - 4 x + 1$ 的值；

(2)、已知 $a = 1 + \sqrt{2}$ ， $b = 1 - \sqrt{2}$ ，求代数式 $a^{2} - b^{2}$ 的值.

查看试题解析
18. 如图，已知 $B E$ ∥ $D F$ ，点A，C在直线 $E F$ 上， $∠ A D F = ∠ C B E$ ， $A F = C E$ ，
求证：四边形 $D E B F$ 是平行四边形.

查看试题解析
19. 如图(1)是用硬纸板做成的两个全等的直角三角形，两直角边的长分别为 $a$ 和 $b ，$ 斜边长为 $c ，$ 图(2)是以 $c$ 为直角边的等腰直角三角形.请你开动脑筋，将它们拼成一个直角梯形.

(1)、在图(3)处画出拼成的这个图形的示意图；

(2)、利用(1)画出的图形证明勾股定理.

查看试题解析
20. 如图，由6个形状、大小完全相同的小矩形组成大矩形网格，小矩形的顶点称为这个矩形网格的格点，由格点构成的四边形称为格点四边形，请按要求作图(标出所画图形的顶点字母).

(1)、在图1中画出一个格点正方形；

(2)、在图2中画出一个一般的格点平行四边形(非菱形、矩形).

查看试题解析
21. 如图，一架6.5m长的梯子AB斜靠在一竖直的墙AO上，这时BO为2.5m.如果将梯子的低端B外移1.4m，顶端A沿着墙壁也下滑1.4m吗?

查看试题解析
22. 如图，平行四边形ABCD的对角线AC， BD相交于点O，且AE∥BD， BE∥AC， OE= CD.

(1)、求证：四边形ABCD是菱形；

(2)、若AD=2，则当四边形ABCD的形状是时，四边形AOBE的面积取得最大值是.

查看试题解析
23. 如图1，在正方形ABCD中，P是对角线BD上的点，点E在AB上，且PA=PE．

(1)、求证：PC=PE；

(2)、求∠CPE的度数；

(3)、如图2，把正方形ABCD改为菱形ABCD，其他条件不变，试探究∠CPE与∠ABC之间的数量关系，并说明理由．

查看试题解析